Dans cet article, nous expliquons ce que sont les fonctions symétriques (fonctions paires et impaires) et comment étudier la symétrie d’une fonction. Vous pourrez également voir les propriétés de ces types de fonctions et, enfin, vous pourrez vous entraîner avec des exercices résolus pas à pas de fonctions symétriques.
Qu’est-ce qu’une fonction symétrique ?
Une fonction symétrique est une fonction dans laquelle un axe de symétrie peut être trouvé dans sa représentation graphique. Il existe deux types de fonctions symétriques : les fonctions paires, symétriques par rapport à l’axe Y, et les fonctions impaires, symétriques par rapport à l’origine des coordonnées.
Rappelez-vous qu’un axe de symétrie est une ligne imaginaire qui divise tout élément en deux parties de sorte que leurs points opposés soient équidistants l’un de l’autre.
même des fonctions
Les fonctions paires sont des fonctions symétriques par rapport à l’axe des ordonnées, c’est-à-dire que l’axe Y est un axe de symétrie de la fonction.
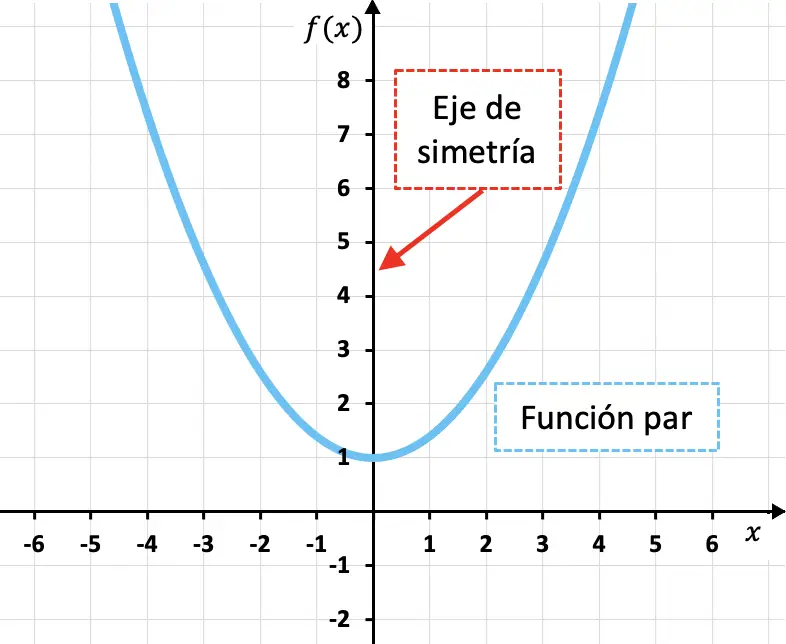
Comme vous pouvez le voir dans la fonction quadratique illustrée ci-dessus, l’image d’une fonction paire pour toute valeur de la variable indépendante (x) est équivalente à l’image de la fonction pour la valeur opposée (-x). Autrement dit, mathématiquement, une fonction est paire si elle remplit la condition suivante :
![]()
Les fonctions paires sont un type de fonctions symétriques, voyons maintenant à quoi ressemblent les fonctions impaires.
fonctions impaires
Les fonctions impaires sont les fonctions symétriques par rapport à l’origine des coordonnées, c’est-à-dire par rapport au point (0,0).
Ci-dessous, vous pouvez voir une fonction impaire représentée graphiquement :
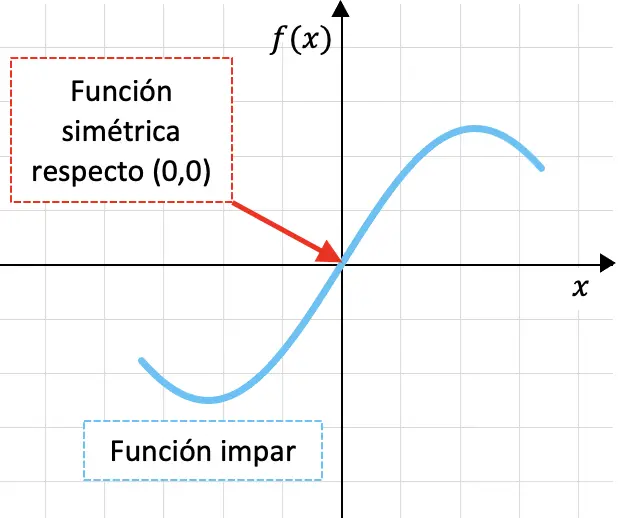
Le fait qu’une fonction soit symétrique par rapport à l’origine des coordonnées signifie que si nous plions le graphe de la fonction d’abord par l’axe OY puis par l’axe OX, le graphe de la fonction se chevaucherait.
Algébriquement, une fonction est impaire si la relation suivante entre ses images est satisfaite :
![]()
Connaître la symétrie d’une fonction est très utile pour la représenter, car ne connaissant qu’une moitié du graphe on peut tracer rapidement l’autre partie.
Comment trouver la symétrie d’une fonction
Pour étudier la symétrie d’une fonction, il faut calculer l’image de
![]() , c’est-à-dire qu’il faut calculer
, c’est-à-dire qu’il faut calculer![]() Ainsi, selon le résultat de l’image, la symétrie de la fonction sera :
Ainsi, selon le résultat de l’image, la symétrie de la fonction sera :
- s’il est rempli
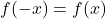 , la fonction est paire et donc symétrique par rapport à l’axe Y.
, la fonction est paire et donc symétrique par rapport à l’axe Y. - s’il est rempli
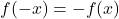 , la fonction est impaire et donc symétrique par rapport à l’origine des coordonnées.
, la fonction est impaire et donc symétrique par rapport à l’origine des coordonnées. - Si aucune des conditions ci-dessus n’est remplie, il s’agit d’une fonction asymétrique (elle n’a pas d’axe de symétrie).
Par exemple, analysons la symétrie de la fonction cubique suivante :
![]()
Pour étudier la symétrie de la fonction, on calcule
![]()
![]()
L’expression algébrique obtenue est équivalente à l’expression de la fonction d’origine mais a changé de signe, ou en d’autres termes, l’égalité suivante est satisfaite :
![]()
La fonction est donc impaire et donc symétrique par rapport à l’origine des coordonnées (0,0).
Propriétés des fonctions symétriques
Les fonctions symétriques ont les caractéristiques suivantes :
- La somme de deux fonctions paires/impaires est égale à une autre fonction paire/impaire.
- Le produit de deux fonctions paires ou de deux fonctions impaires donne une fonction paire.
- La dérivée d’une fonction paire/impaire est une fonction paire/impaire.
- La composition entre deux fonctions pair/impair équivaut à une fonction pair/impair.
- La seule fonction à la fois paire et impaire, c’est-à-dire symétrique par rapport à l’axe OY et par rapport à l’origine, est la fonction
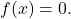
Problèmes résolus de la symétrie d’une fonction
Exercice 1
Trouvez la symétrie de la fonction suivante :
![]()
Pour calculer la symétrie de la fonction, nous devons évaluer
![]()
![]()
Toute puissance d’un nombre négatif élevée à un exposant pour donne un nombre positif, donc dans ce cas l’équation suivante est vraie :
![]()
La fonction est donc paire et, par conséquent, elle est symétrique par rapport à l’axe des ordonnées (axe Y).
Exercice 2
Étudiez la symétrie de la fonction rationnelle suivante :
![]()
Pour déterminer la symétrie de la fonction, on fait
![]()
![]()
Dans ce problème, aucune condition de symétrie n’est remplie, car l’image de
![]() n’est pas égal à
n’est pas égal à![]() ni à
ni à ![]()
![]()
La fonction n’a donc pas d’axe de symétrie, mais est plutôt une fonction asymétrique.
Exercice 3
Calculez la symétrie de la fonction suivante :
![]()
Pour analyser la symétrie de la fonction, nous devons calculer
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
Dans ce cas, l’expression obtenue est comme l’expression originale mais avec un changement de signe, donc l’équation suivante est remplie :
![]()
La fonction est donc impaire et donc symétrique par rapport à l’origine des coordonnées (0,0).