Sur cette page, vous trouverez l’explication de ce qu’est le binôme de Newton (ou théorème du binôme) et quelle est sa formule. Vous pouvez également voir comment cela peut être simplifié avec le triangle de Tartaglia (ou de Pascal). De plus, vous trouverez des exercices résolus étape par étape pour le binôme de Newton et toutes ses propriétés. Enfin, nous expliquerons les curiosités derrière l’origine de ce théorème très particulier.
Qu’est-ce que le binôme de Newton ?
En mathématiques, le binôme de Newton , également connu sous le nom de théorème du binôme , est une formule qui permet de calculer facilement la puissance d’un binôme. Autrement dit, le binôme de Newton consiste en une formule avec laquelle des expressions algébriques de la forme (a+b) n peuvent être résolues.
Évidemment, ce théorème porte le nom du physicien, mathématicien et philosophe Sir Isaac Newton. Il existe cependant une certaine controverse à cet égard puisque des textes du Moyen-Orient ont été trouvés où ce théorème était déjà utilisé. Ci-dessous, nous discuterons en profondeur de l’origine de cette formule mathématique.
Formule binomiale de Newton
Comme nous l’avons vu dans la définition du binôme de Newton, ce théorème est utilisé pour résoudre les puissances des binômes. Mais… comment le binôme de Newton est-il appliqué ? Ou, en d’autres termes, quelle est la formule du binôme de Newton ?
La formule mathématique du binôme de Newton est la suivante :
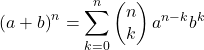
Ou équivalent:
![]()
La formule est un peu complexe pour comprendre le concept du binôme de Newton, nous avons donc présenté ci-dessous les puissances des binômes du degré le plus bas afin que vous puissiez mieux le comprendre :

Comme vous pouvez le voir, lors du développement d’un binôme , les exposants du premier terme (a) diminuent tandis que les exposants du deuxième terme (b) augmentent , tout comme l’élément inférieur des nombres combinatoires augmente.
Par conséquent, pour utiliser le théorème binomial, vous devez savoir résoudre un nombre combinatoire, c’est-à-dire l’expression algébrique du type
![]() . Donc, avant d’examiner des exemples de calcul d’un binôme de Newton, passons brièvement en revue les nombres combinatoires.
. Donc, avant d’examiner des exemples de calcul d’un binôme de Newton, passons brièvement en revue les nombres combinatoires.
nombre combinatoire
Pour déterminer un nombre combinatoire (ou coefficient binomial) il faut appliquer la formule suivante :
![]()
Où
![]() et
et![]() Ce sont des nombres factoriels . Rappelons également qu’un nombre factoriel se calcule en multipliant tous les entiers positifs de 1 par ledit nombre :
Ce sont des nombres factoriels . Rappelons également qu’un nombre factoriel se calcule en multipliant tous les entiers positifs de 1 par ledit nombre :
![]()
A titre d’exemple, nous allons trouver un nombre combinatoire pour que vous puissiez voir comment cela se fait :
![]()
Les nombres combinatoires peuvent également être déterminés via la calculatrice avec la touche
![]()
Exemples de binôme de Newton
Maintenant que nous savons en quoi consiste le théorème binomial, voyons comment appliquer la formule binomiale de Newton à l’aide de deux exemples numériques.
Exemple 1
- Appliquez le binôme de Newton pour calculer la puissance du binôme suivant :
![]()
Évidemment, puisque ce binôme est au carré, il pourrait aussi être résolu avec les formules des identités notables ( comment résoudre les identités notables ), mais nous le calculerons avec le théorème du binôme comme exemple.
Tout d’abord, il faut appliquer la formule binomiale de Newton :
![]()
Dans ce cas n=2, donc :
![]()
Regardez bien, au début on élève le premier terme (x) au maximum possible, qui dans ce cas est 2. Par contre, on élève le deuxième terme (3) au minimum possible, qui est toujours 0. Mais à mesure que nous nous dirigeons vers la droite, nous devons élever le premier terme à un nombre inférieur à celui d’avant et le deuxième terme à un nombre supérieur à celui d’avant.
Calculons maintenant les nombres combinatoires :
![]()
On résout les puissances :
![]()
Et enfin, on calcule les multiplications :
![]()
Exemple 2
Nous allons maintenant résoudre un problème légèrement plus difficile.
- Appliquez la formule binomiale de Newton pour trouver la puissance du binôme suivant :
![]()
La formule du théorème du binôme est :
![]()
Dans ce cas n=3, donc :
![]()
On calcule les nombres combinatoires :
![]()
Maintenant, nous résolvons les puissances, pour cela il est important que vous vous souveniez des deux propriétés suivantes :
• Lorsqu’un monôme est élevé à un exposant, le coefficient et la variable sont élevés au même exposant →
![]()
• Tout terme porté à 0 donne 1 →![]()
On retrouve donc les puissances à travers ces 2 propriétés :
![]()
![]()
Et enfin, on multiplie les termes :
![]()
Binôme de Newton et triangle de Tartaglia (ou Pascal)
Comme vous l’avez vu dans les exemples ci-dessus, calculer des nombres combinatoires est un peu fastidieux. C’est pourquoi nous allons vous apprendre une astuce pour que vous n’ayez pas à résoudre les nombres combinatoires, puisque vous pouvez directement savoir combien ils valent en utilisant le triangle de Tartaglia, également connu sous le nom de triangle de Pascal.
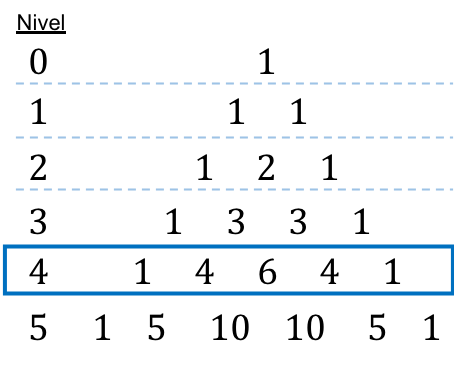
Au cas où vous ne sauriez pas de quoi il s’agit, le triangle de Tartaglia , également appelé triangle de Pascal , est une représentation mathématique de nombres disposés en forme de triangle.
Pour construire le triangle Tartaglia ou Pascal, nous devons commencer par le sommet du triangle, qui est toujours un 1, puis les numéros des lignes ci-dessous sont déterminés. Chaque nombre des lignes suivantes est égal à la somme des deux nombres immédiatement au-dessus, à l’exception des extrémités des lignes qui valent toujours 1.

Ainsi, chacun de ces nombres dans le triangle de Tartaglia correspond au résultat d’un nombre combinatoire, regardez la figure suivante :

Par exemple, le coefficient binomial
![]() équivaut à 3, car dans le triangle de Tartaglia il y a un 3 à sa position.
équivaut à 3, car dans le triangle de Tartaglia il y a un 3 à sa position.
On peut donc utiliser le triangle de Tartaglia (ou de Pascal) pour résoudre le binôme de Newton beaucoup plus rapidement, puisqu’il nous épargne les calculs de nombres combinatoires.
Par exemple, si l’on veut faire la potentialisation suivante d’un binôme :
![]()
En appliquant la règle du binôme de Newton on obtient l’expression algébrique suivante :
![]()
Eh bien, au lieu de calculer les nombres combinatoires un par un, nous pouvons simplement remplacer chaque nombre combinatoire par son coefficient correspondant du triangle de Tartaglia. Dans ce cas le binôme est élevé au 3ème, il correspond donc au troisième niveau du triangle :

![]()
Et maintenant il ne nous reste plus qu’à faire les opérations restantes :
![]()
![]()
Comme vous pouvez le constater, le triangle de Tartaglia (ou de Pascal) est utilisé pour calculer le binôme de Newton de manière plus simple et plus rapide, comme nous l’avons montré. C’est pourquoi nous vous recommandons de l’utiliser.
Pour résumer tout ce que nous avons vu jusqu’à présent, nous vous laissons une image qui montre à quoi ressemblent les expressions des binômes de Newton avec les nombres du triangle de Tartaglia (ou Pascal) :

Binôme de Newton négatif : puissance d’une soustraction
Jusqu’à présent, tous les exemples du binôme de Newton que nous avons résolus étaient des ajouts. En revanche, lorsque l’un des deux termes du binôme présente un signe négatif, la procédure reste similaire mais change un peu.
Lorsqu’un des termes du binôme est négatif, c’est-à-dire qu’il s’agit d’une soustraction du type (ab) n , les signes du développement du binôme de Newton doivent alterner sous la forme + – + – + – + – …
Ci-dessous nous avons développé les puissances des binômes négatifs des 5 premiers degrés avec le théorème du binôme et avec les coefficients du triangle de Tartaglia déjà en place, afin que vous puissiez trouver directement l’expression binomiale dont vous avez besoin :

Propriétés du binôme de Newton
Les expressions binomiales de Newton répondent aux caractéristiques suivantes :
- Décomposer le binôme de Newton aboutit toujours à un terme de plus que le degré du binôme. Ou en d’autres termes, pour le binôme
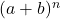 ils sont atteints
ils sont atteints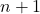 termes.
termes. - Les pouvoirs de l’élément
 Commencer avec
Commencer avec et ils diminuent jusqu’à atteindre 0 au dernier trimestre.
et ils diminuent jusqu’à atteindre 0 au dernier trimestre. - Les pouvoirs de l’élément
 ils vont dans l’autre sens : ils commencent à 0 et augmentent jusqu’à atteindre
ils vont dans l’autre sens : ils commencent à 0 et augmentent jusqu’à atteindre au dernier mandat.
au dernier mandat. - Pour chaque élément du binôme de Newton, la somme des exposants de
 et
et est égal à
est égal à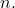
- Le coefficient du premier terme de l’expression binomiale de Newton est toujours 1 (positif) et le deuxième coefficient est équivalent à l’exposant du binôme (positif ou négatif).
Calculer le kième terme du binôme de Newton
Bien que cela soit inhabituel, nous pouvons parfois rencontrer des problèmes dans lesquels, au lieu de faire le développement binomial de Newton, on nous demande de déterminer le kème terme du binôme de Newton, c’est-à-dire le terme qui occupe la position k .
Ainsi, pour calculer le terme qui occupe la place k dans le binôme de Newton, il faut utiliser une formule, qui dépend si le binôme est une addition ou une soustraction :
- Si le binôme de Newton est positif, la valeur du kème terme est calculée avec la formule suivante :
![]()
- Si le binôme de Newton est négatif, la valeur du kème terme est déterminée avec la formule suivante :
![]()
A titre d’exemple, nous allons trouver le quatrième terme du binôme de degré 5 suivant :
![]()
Puisqu’il s’agit d’un binôme composé d’une somme, on applique la première formule :
![]()
On remplace les variables de la formule par leurs valeurs correspondantes :
![]()
Et nous faisons les opérations :
![]()
![]()
![]()
Et de cette façon, nous avons calculé le quatrième terme du développement binomial de Newton sans avoir besoin de calculer tous les autres termes.
Exercices résolus pour le binôme de Newton
Maintenant que nous avons expliqué en quoi consiste le théorème du binôme, nous vous laissons avec plusieurs exercices résolus étape par étape sur le binôme de Newton afin que vous puissiez vous entraîner. N’oubliez pas également que vous pouvez nous laisser toutes vos questions ou suggestions dans les commentaires.
Exercice 1
Développez la puissance binomiale suivante en utilisant le théorème binomial :
![]()
Nous utilisons d’abord la formule binomiale de Newton :
![]()
Puisque le binôme est élevé à la puissance 3, on regarde le troisième niveau du triangle de Tartaglia pour trouver directement les nombres combinatoires :

![]()
Nous effectuons les pouvoirs :
![]()
Et enfin on multiplie :
![]()
![]()
Exercice 2
Calculez la puissance suivante avec la formule binomiale de Newton :
![]()
Tout d’abord, nous appliquons la formule binomiale de Newton :
![]()
Puisque le binôme est au cube, on regarde le troisième niveau du triangle de Pascal pour connaître directement les valeurs des nombres combinatoires :

![]()
On calcule les puissances des monômes :
![]()
Et, pour finir, on fait les multiplications :
![]()
![]()
Exercice 3
Développez l’expression polynomiale suivante à l’aide de la formule binomiale de Newton :
![]()
Tout d’abord, nous utilisons la formule binomiale de Newton. Mais comme on a une soustraction à l’intérieur des parenthèses, il faut alterner les signes des coefficients de chaque terme :
![]()
Puisque le binôme est élevé à la puissance trois, on regarde le troisième niveau du triangle de Tartaglia pour calculer directement les nombres combinatoires :

![]()
Nous effectuons les pouvoirs :
![]()
Et on résout les multiplications :
![]()
![]()
Exercice 4
Trouvez l’expression développée du binôme de Newton suivant avec la formule :
![]()
Il faut appliquer la formule générale du binôme de Newton, mais comme dans ce cas nous avons une soustraction entre parenthèses, nous devons alterner les signes de chaque terme :
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7a8620bd23846e1f98f7646cbd51dbc5_l3.png)
Puisque le binôme est élevé au quatrième, on regarde le niveau 4 du triangle de Tartaglia pour trouver directement les nombres combinatoires :
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-128e8baa45ddd7d74703c9dfd4a19b06_l3.png)
Nous réalisons toutes les puissances :
![]()
Et, pour finir, on résout les multiplications :
![]()
![]()
Exercice 5
Déterminez le septième terme du développement de l’expression binomiale suivante :
![]()
Puisqu’il s’agit d’un binôme négatif, il faut utiliser la formule suivante :
![]()
Nous voulons déterminer le terme 7 et le binôme est élevé à la puissance 10, donc en substituant les valeurs dans la formule il devient :
![]()
Il suffit donc d’opérer pour connaître le terme :
![Rendered by QuickLaTeX.com \begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ded0622cbba2bff0563c2f9982c05142_l3.png)
Histoire du binôme de Newton
Bien que l’origine du théorème du binôme soit attribuée au célèbre scientifique anglais Isaac Newton (1642-1727), en réalité la première formulation du théorème a été découverte pour la première fois par l’ingénieur persan Al-Karijí vers l’an 1000. Et elle On a même découvert qu’au XIIIe siècle les mathématiciens chinois Yang Hui et Chuh Shih-Chieh connaissaient déjà des expansions binomiales de petits degrés.
Plus tard, au XVIIe siècle, Newton s’est appuyé sur les fondations posées par les mathématiciens précédents pour étendre le théorème du binôme. En utilisant les méthodes d’interpolation et d’extrapolation du mathématicien John Walls et les concepts d’exposants généralisés, il parvient à transformer une expression polynomiale en une série infinie.
Vers 1665, Newton réussit à démontrer que l’exposant n du théorème du binôme pouvait aussi être un exposant rationnel, c’est-à-dire que la puissance d’un binôme peut également être résolue si l’exposant est une fraction. D’un autre côté, il a également fait la preuve dans le cas d’un exposant négatif. Et, étonnamment, il a découvert que les développements des deux expressions sont des séries infinies de termes.
C’est avec cette découverte que Newton a commencé à remettre en question la relation entre les séries infinies et les expressions polynomiales finies, et en a déduit que mathématiquement des opérations peuvent être effectuées avec des séries infinies de la même manière que les expressions polynomiales finies. Bien que Newton n’ait jamais publié ce théorème, John Walls finit par le faire en 1685, accordant cette découverte à Newton.