Vecteurs perpendiculaires ou orthogonaux

Sur cette page vous trouverez tout ce qui concerne les vecteurs perpendiculaires (ou orthogonaux) : ce qu’ils sont, quand deux vecteurs sont orthogonaux, comment trouver un vecteur perpendiculaire à un autre, les propriétés des vecteurs perpendiculaires,… De plus, vous pourrez voir plusieurs exemples et exercices résolus de vecteurs perpendiculaires ou orthogonaux.

Que sont deux vecteurs perpendiculaires ou orthogonaux ?

En mathématiques, deux vecteurs sont orthogonaux (ou perpendiculaires ) lorsqu’ils forment un angle droit (90º) l’un par rapport à l’autre.

Dans la représentation graphique suivante, vous pouvez voir deux vecteurs perpendiculaires :

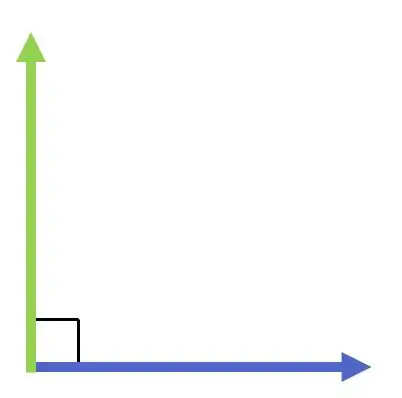
lorsque deux vecteurs sont dits perpendiculaires ou orthogonaux

En revanche, la perpendicularité de deux vecteurs dépend uniquement de leur direction, et non de leur module (ou grandeur) ou, évidemment, de leur direction. Autrement dit, deux vecteurs seront perpendiculaires s’ils font un angle de 90 degrés, qu’ils aient ou non la même longueur.

Comment savoir si deux vecteurs sont orthogonaux ou perpendiculaires ?

Comme nous venons de le voir, graphiquement il est très facile de voir si deux vecteurs sont perpendiculaires. Cependant, vous pouvez également déterminer si deux vecteurs sont orthogonaux sans les représenter graphiquement :

Numériquement, deux vecteurs sont orthogonaux ou perpendiculaires lorsque leur produit scalaire est égal à zéro (0).

Par exemple, nous allons montrer que les deux vecteurs suivants sont perpendiculaires sans les représenter graphiquement :

$\vv{\text{u}}=(3,2) \qquad\vv{\text{v}}=(-2,3)$

Pour vérifier qu’il s’agit de vecteurs perpendiculaires (ou orthogonaux), on applique la formule du produit scalaire :

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(3,2)\cdot (-2,3) \\[1.5ex]&=3\cdot (-2) + 2 \cdot 3 \\[1.5ex] & = -6+6 \\[1.5ex] & =\bm{0} \end{aligned}$

Le résultat du produit scalaire des deux vecteurs est nul, il s’agit donc de deux vecteurs orthogonaux (ou perpendiculaires) l’un à l’autre.

$\vv{\text{u}}\bm{\perp} \vv{\text{v}}$

Notez que deux vecteurs sont indiqués comme étant perpendiculaires par le symbole

$\bm{\perp}}.$

Par conséquent, le produit scalaire entre deux vecteurs perpendiculaires est nul. Or, le produit vectoriel de deux vecteurs (un autre type de multiplication entre vecteurs) donne l’inverse : un vecteur perpendiculaire aux deux autres. Par conséquent, il est important de savoir distinguer les deux types d’opérations, vous pouvez voir les différences entre elles dans les propriétés du produit croisé .

Comment un vecteur perpendiculaire ou orthogonal à un autre est-il calculé ?

La façon la plus simple de calculer un vecteur perpendiculaire à un autre dans le plan (dans R2) est d’entrelacer les deux coordonnées du vecteur et également de changer le signe en un.

Et pour obtenir un vecteur perpendiculaire à un autre dans l’espace (dans R3) il faut intercaler deux coordonnées l’une avec l’autre, puis changer le signe de l’une d’elles et, enfin, mettre à zéro la coordonnée restante.

Pour que vous puissiez voir les différences de calcul d’un vecteur orthogonal à un autre selon qu’ils ont 2 ou 3 coordonnées, nous allons résoudre un exercice avec chaque type de vecteur.

Trouver un vecteur perpendiculaire ou orthogonal dans le plan cartésien

Déterminez un vecteur perpendiculaire au vecteur bidimensionnel suivant :

$\vv{\text{v}}=(4,1)$

Puisqu’il s’agit d’un vecteur à deux composantes seulement, pour obtenir un vecteur perpendiculaire, il faut alterner ses composantes et nier l’une d’entre elles :

$\vv{\mathbf{u}}\bm{=(-1,4)}$

Nous pouvons vérifier à partir de la formule du produit scalaire qu’il s’agit bien de vecteurs perpendiculaires :

$\vv{\text{v}} \cdot \vv{\text{u}}=(4,1)\cdot (-1,4) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Déterminer un vecteur perpendiculaire ou orthogonal dans l’espace cartésien

Calculer un vecteur orthogonal au vecteur tridimensionnel suivant :

$\vv{\text{v}}=(2,3,-1)$

Dans ce cas, nous avons un vecteur à trois composantes, donc pour obtenir un vecteur perpendiculaire, nous devons alterner deux de ses composantes, changer le signe de l’une d’entre elles et convertir la coordonnée restante en zéro :

$\vv{\mathbf{u}}\bm{=(3,-2,0)}$

On peut vérifier avec la formule du produit scalaire qu’il s’agit bien de vecteurs orthogonaux :

$\vv{\text{v}} \cdot \vv{\text{u}}=(2,3,-1)\cdot (3,-2,0) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Propriétés des vecteurs perpendiculaires et orthogonaux

Les vecteurs perpendiculaires ont les caractéristiques suivantes :

Relation symétrique : Si un vecteur est perpendiculaire à un autre vecteur, alors ce vecteur est également perpendiculaire au premier vecteur.

$\vv{\text{u}} \bm{\perp} \vv{\text{v}} \ \longrightarrow \ \vv{\text{v}} \bm{\perp} \vv{\text{u}}$

Propriété irréflexive : Évidemment, aucun vecteur ne peut être perpendiculaire à lui-même.

$\vv{\text{v}} \ \cancel{\bm{\perp}}} \ \vv{\text{v}}$

En géométrie euclidienne (dans R2), toute paire de vecteurs perpendiculaires à un troisième vecteur doit nécessairement être parallèle. Autrement dit, si un vecteur est perpendiculaire à un autre vecteur et que ce vecteur est également perpendiculaire à un troisième vecteur, les premier et dernier vecteurs sont parallèles. Cela est dû au cinquième postulat d’Euclide .

D’autre part, il faut aussi savoir que grâce à ces propriétés la règle du tire-bouchon peut être utilisée. Cette technique permet de calculer facilement un type d’opération vectorielle qui, sans cette règle, prendrait beaucoup de temps à résoudre. Vous pouvez voir en quoi cela consiste en cliquant sur l’explication de la règle du tire-bouchon .

Concepts liés aux vecteurs perpendiculaires ou orthogonaux

Il existe deux types de vecteurs très proches des vecteurs perpendiculaires : les vecteurs normaux et les vecteurs orthomarles. Bien qu’ils soient tous liés les uns aux autres, nous voulons préciser en quoi ils diffèrent afin d’éviter toute confusion possible.

Un vecteur normal est un vecteur perpendiculaire à un plan. Ainsi, il peut également être inclus dans le concept d’orthogonalité d’un vecteur, mais dans ce cas, il est perpendiculaire à un plan au lieu d’un autre vecteur.

D’autre part, deux vecteurs orthonormés sont deux vecteurs orthogonaux entre eux et qui, de plus, sont des vecteurs unitaires (de grandeur égale à 1).

Enfin, il convient également de noter qu’il est très courant d’utiliser des bases orthogonales (bases vectorielles formées de vecteurs perpendiculaires entre eux) et même des bases orthonormées . En fait, le repère cartésien est une base orthonormée.