Tous les vecteurs linéairement indépendants et dépendants

Sur cette page, nous expliquons ce que sont les vecteurs linéairement indépendants et linéairement dépendants. Vous pourrez également voir des exemples montrant comment savoir si un ensemble de vecteurs est linéairement dépendant ou indépendant. Et, en plus, vous trouverez des exercices et des problèmes résolus étape par étape sur l’indépendance et la dépendance linéaires.

Que sont les vecteurs linéairement indépendants ?

Un ensemble de vecteurs libres est linéairement indépendant si aucun d’entre eux ne peut être écrit comme une combinaison linéaire des autres.

Autrement dit, étant donné un ensemble de vecteurs

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$ Ceux-ci sont linéairement indépendants si la seule solution de l’équation suivante :

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

Ce sont tous les coefficients

$a_i$ égal à 0 :

$a_1=a_2=\dots = a_n=0$

Géométriquement, deux vecteurs sont linéairement indépendants s’ils n’ont pas la même direction, c’est-à-dire s’ils ne sont pas parallèles.

Par souci de concision, on dit parfois directement qu’ils sont des vecteurs LI. Ou encore que les vecteurs ont une indépendance linéaire.

Que sont les vecteurs linéairement dépendants ?

De toute évidence, les vecteurs linéairement dépendants signifient le contraire des vecteurs linéairement indépendants. Sa définition est donc :

Un ensemble de vecteurs libres du plan est linéairement dépendant si l’un d’entre eux peut être exprimé comme une combinaison linéaire d’autres vecteurs qui forment le système.

Autrement dit, étant donné un ensemble de vecteurs

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$ Ceux-ci sont linéairement dépendants s’il existe une solution de l’équation suivante :

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

dans lequel un certain coefficient

$a_i$ est différent de 0 :

$a_i\neq 0$

L’inverse est également vrai : si un vecteur est une combinaison linéaire d’autres vecteurs, alors tous les vecteurs de l’ensemble sont linéairement dépendants.

De plus, si deux vecteurs sont parallèles, cela implique qu’ils sont linéairement dépendants.

Parfois, ils sont également abrégés et simplement appelés vecteurs LD. Ou même que les vecteurs ont une dépendance linéaire.

Exemple de comment savoir si les vecteurs sont linéairement dépendants ou indépendants

Nous allons ensuite voir un exemple typique de vecteurs linéairement dépendants et indépendants.

Déterminez si les 3 vecteurs tridimensionnels suivants ont une dépendance ou une indépendance linéaire :

$\vv{\text{u}} = (1,5,2)$

$\vv{\text{v}} = (-2,3,-1)$

$\vv{\text{w}} = (4,2,1)$

Tout d’abord, nous devons énoncer la condition de combinaison linéaire :

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

Maintenant, nous remplaçons chaque vecteur par ses coordonnées. Comme zéro, qui correspond au vecteur nul :

$a_1(1,5,2)+a_2(-2,3,-1)+ a_3(4,2,1)=(0,0,0)$

Les coefficients multiplient les vecteurs, donc l’expression suivante est équivalente :

$(a_1,5a_1,2a_1)+(-2a_2,3a_2,-a_2) + (4a_3,2a_3,a_3)=(0,0,0)$

On fait l’addition de vecteurs :

$(a_1-2a_2+4a_3 \ , \ 5a_1+3a_2+2a_3 \ , \ 2a_1-a_2+a_3)=(0,0,0)$

Si on regarde bien, l’expression précédente correspond à 3 équations, puisque chaque coordonnée du vecteur de gauche doit être égale à chaque coordonnée du vecteur de droite. On a donc un système homogène de 3 équations à 3 inconnues :

$\left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}$

La seule chose que nous devons faire est donc de résoudre le système d’équations dont les inconnues sont

$a_1, a_2$ et $a_3.$ Pour ce faire, vous pouvez utiliser n’importe quelle méthode (méthode de substitution, méthode de Gaus, règle de Cramer,…). Cependant, pour savoir si les vecteurs sont LI ou LD il suffit de déterminer s’il existe une solution autre que la solution triviale (tous les coefficients égaux à zéro). Donc:

Si le déterminant de la matrice composée des composantes des vecteurs est différent de zéro, cela signifie que le système d’équations n’a qu’une seule solution ( 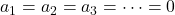$a_1=a_2=a_3=\dots=0$ ) et, par conséquent, les vecteurs sont linéairement indépendants
En revanche, si le déterminant de la matrice composée des composantes des vecteurs est égal à zéro, cela implique que le système d’équations a plus d’une solution et, par conséquent, les vecteurs sont linéairement dépendants .

Donc la seule chose qui doit être calculée est le déterminant avec les coordonnées des vecteurs (comme c’est un déterminant 3×3, il peut être résolu avec la règle de Sarrus). Ce déterminant correspond aux coefficients du système d’équations précédent :

$\displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}$

Dans ce cas, le déterminant est différent de 0, donc les vecteurs sont linéairement indépendants .

Par conséquent, la seule solution possible au système d’équations est la solution triviale avec toutes les inconnues égales à zéro :

$a_1=a_2=a_3=0$

Propriétés des vecteurs linéairement dépendants et indépendants

La dépendance linéaire ou l’indépendance des vecteurs présente les caractéristiques suivantes :

Deux vecteurs proportionnels sont parallèles et sont donc linéairement dépendants car ils ont la même direction.

De même, si deux vecteurs n’ont pas la même direction ou ne sont pas proportionnels, ils sont linéairement indépendants.

Trois vecteurs coplanaires (qui sont dans le même plan) sont linéairement indépendants.

Le vecteur nul 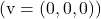$(\vv{\text{v}}=(0,0,0))$ est linéairement dépendant de n’importe quel vecteur.

Un ensemble de vecteurs linéairement indépendants génère un espace vectoriel et forme une base vectorielle. Si les trois vecteurs sont perpendiculaires, c’est une base orthogonale. Et si en plus son module est égal à 1, cela correspond à une base orthonormée.

Exercices de dépendance et d’indépendance linéaires résolus

Ci-dessous, vous avez plusieurs exercices résolus sur des vecteurs linéairement dépendants et indépendants à pratiquer.

Exercice 1

Déterminez si les vecteurs suivants sont linéairement dépendants ou indépendants :

$\vv{\text{u}} = (1,-2,1)$

$\vv{\text{v}} = (2,1,3)$

$\vv{\text{w}} = (5,-1,1)$

Voir la solution

Nous posons d’abord la condition de combinaison linéaire :

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,-2,1)+a_2(2,1,3)+ a_3(5,-1,1)=(0,0,0)$

$(a_1,-2a_1,a_1)+(2a_2,a_2,3a_2) + (5a_3,-a_3,a_3)=(0,0,0)$

$(a_1+2a_2+5a_3 \ , \ -2a_1+a_2-a_3 \ , \ a_1+3a_2+a_3)=(0,0,0)$

L’égalité précédente correspond au système d’équations linéaires suivant :

$\left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}$

Une fois que nous avons énoncé le système d’équations, nous résolvons le déterminant de la matrice avec ses termes :

$\displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}$

Dans ce cas, le déterminant est différent de 0, donc les trois vecteurs sont linéairement indépendants les uns des autres.

Exercice 2

Classez les vecteurs suivants comme linéairement dépendants ou indépendants :

$\vv{\text{u}} = (1,4,3)$

$\vv{\text{v}} = (-2,0,2)$

$\vv{\text{w}} = (3,-1,-4)$

Voir la solution

Tout d’abord nous posons l’équation de la combinaison linéaire :

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,4,3)+a_2(-2,0,2)+ a_3(3,-1,-4)=(0,0,0)$

$(a_1,4a_1,3a_1)+(-2a_2,0,2a_2) + (3a_3,-a_3,-4a_3)=(0,0,0)$

$(a_1-2a_2+3a_3 \ , \ 4a_1-a_3 \ , \ 3a_1+2a_2-4a_3)=(0,0,0)$

De l’égalité précédente on obtient le système d’équations homogène suivant :

$\left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}$

Une fois que nous avons énoncé le système d’équations, nous résolvons le déterminant de la matrice avec les coordonnées des vecteurs :

$\displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}$

Dans ce cas, le déterminant est équivalent à 0, donc les trois vecteurs dépendent linéairement les uns des autres.

Exercice 3

Pour les trois vecteurs suivants, indiquez quelles paires de vecteurs sont linéairement dépendantes et quelles paires sont linéairement indépendantes.

$\vv{\text{u}} = (1,2,-2) \qquad \vv{\text{v}} = (2,4,-3) \qquad \vv{\text{w}} = (-4,-8,6)$

Voir la solution

Le moyen le plus simple de savoir si une paire de vecteurs est linéairement dépendants ou indépendants est de vérifier s’ils sont proportionnels.

Nous vérifions d’abord le vecteur

$\vv{\text{u}}$ avec le vecteur $\vv{\text{v}} :$

$\cfrac{1}{2} = \cfrac{2}{4} \neq \cfrac{-2}{-3} \ \longrightarrow \ \text{LI}$

Deuxièmement, nous vérifions le vecteur

$\vv{\text{u}}$ avec le vecteur $\vv{\text{w}} :$

$\cfrac{1}{-4} = \cfrac{2}{-8} \neq \cfrac{-2}{6} \ \longrightarrow \ \text{LI}$

Enfin, nous testons le vecteur

$\vv{\text{v}}$ avec le vecteur $\vv{\text{w}} :$

$\cfrac{2}{-4} = \cfrac{4}{-8} = \cfrac{-3}{6} = -\cfrac{1}{2} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \text{LD}$

Ainsi, la seule paire de vecteurs qui dépendent linéairement les uns des autres est

$\vv{\text{v}}$ et $\vv{\text{w}}.$ De plus, leur relation est la suivante :

$\vv{\text{v}}= -\cfrac{1}{2} \vv{\text{w}}$

Ou équivalent:

$\vv{\text{w}}= -2\vv{\text{v}}$

En revanche, les autres paires de vecteurs sont linéairement indépendantes.

Exercice 4

Étudiez la dépendance linéaire ou l’indépendance des 4 vecteurs suivants entre eux :

$\vv{\text{u}} = (0,1,2)$

$\vv{\text{v}} = (-1,-2,0)$

$\vv{\text{w}} = (4,1,-1)$

$\vv{\text{x}} = (-2,-3,2)$

Voir la solution

Nous posons d’abord la condition de combinaison linéaire :

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}+a_4\vv{\text{x}}=0$

$a_1(0,1,2)+a_2(-1,-2,0)+ a_3(4,1,-1)+a_4(-2,-3,2)=(0,0,0)$

$(0,a_1,2a_1)+(-a_2,-2a_2,0) +(4a_3,a_3,-a_3)+(-2a_4,-3a_4,2a_4)=(0,0,0)$

$(-a_2+4a_3-2a_4\ , \ a_1-2a_2+a_3-3a_4 \ , \ 2a_1-a_3+2a_4)=(0,0,0)$

Dans ce cas nous avons un système de 3 équations à 4 inconnues :

$\left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}$

Nous ne pouvons pas résoudre le déterminant de la matrice système entière, puisque seules les matrices carrées peuvent être déterminées. Il faut donc calculer toutes les combinaisons possibles de déterminants 3×3 et voir si l’un d’entre eux est égal à 0, auquel cas les vecteurs seront linéairement dépendants, par contre, si tous les déterminants sont différents de 0 les 4 vecteurs sera linéairement indépendant.

On calcule le déterminant des coefficients

$a_1, a_2$ et $a_3:$

$\displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}$

Le déterminant des 3 premiers coefficients (ou des 3 premiers vecteurs) est différent de zéro. Alors maintenant on essaie avec le déterminant des coefficients

$a_1, a_2$ et $a_4:$

$\displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}$

Nous avons obtenu un déterminant nul, il n’est donc pas nécessaire de calculer les autres déterminants car on sait déjà que les 4 vecteurs sont linéairement dépendants .