Vecteurs coplanaires (ou coplanaires)

Sur cette page, vous découvrirez ce que sont les vecteurs coplanaires et comment savoir si 2, 3, 4 vecteurs ou plus sont coplanaires. De plus, vous pourrez voir des exemples et des exercices résolus pas à pas de vecteurs coplanaires.

Que sont les vecteurs coplanaires ?

En géométrie analytique, la signification des vecteurs coplanaires (ou coplanaires) est la suivante :

Les vecteurs coplanaires sont les vecteurs qui appartiennent au même plan.

Par conséquent, deux vecteurs sont toujours coplanaires car un plan peut être formé avec aussi peu que 2 vecteurs. Par contre, lorsqu’il y a 3, 4 vecteurs ou plus, il se peut que l’un des vecteurs ne soit pas contenu dans le même plan et, par conséquent, qu’ils ne soient pas coplanaires.

exemples de vecteurs coplanaires ou coplanaires

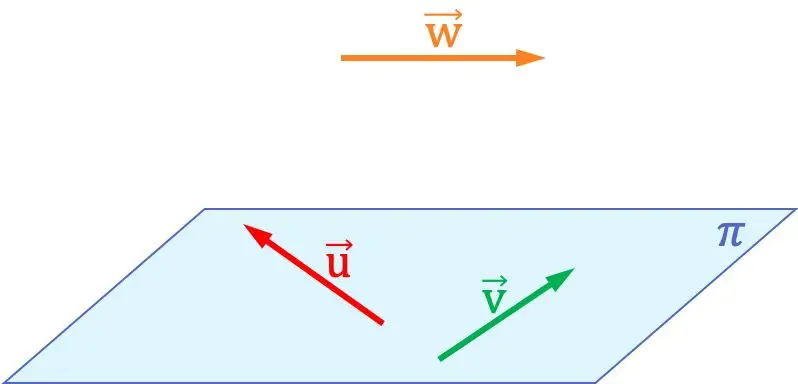
Par exemple, dans la représentation graphique ci-dessus, vous pouvez voir que les vecteurs

$\vv{\text{u}}$ et $\vv{\text{v}}$ ils sont coplanaires entre eux, puisqu’ils sont contenus dans le même plan. Par contre, ces deux vecteurs ne sont pas coplanaires avec le vecteur $\vv{\text{w}}$ , car aucun plan ne peut être formé dans l’espace qui contient les trois vecteurs.

De cette propriété on peut déduire que si 3 vecteurs ou plus sont coplanaires, les points qui définissent lesdits vecteurs (début et fin du vecteur) sont également des points coplanaires.

Quand les vecteurs sont-ils coplanaires ?

Comme nous l’avons vu dans la définition des vecteurs coplanaires (ou coplanaires), deux vecteurs sont toujours coplanaires, mais plus de deux vecteurs n’ont pas à respecter la relation de coplanarité.

Ainsi, il existe plusieurs méthodes pour déterminer si trois vecteurs ou plus sont coplanaires :

Si le produit mixte de trois vecteurs (ou triple produit scalaire) est égal à zéro, cela signifie que les trois vecteurs sont coplanaires. Si vous n’êtes pas très clair sur la façon dont cette opération est calculée, je vous recommande de jeter un œil à ce qu’est le produit mixte de trois vecteurs , vous trouverez ici l’explication ainsi que des exemples et des exercices résolus.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] =0$

Si un ensemble de vecteurs peut être exprimé comme une combinaison linéaire de deux vecteurs, cela implique qu’ils sont coplanaires, ce qui signifie que 3 vecteurs ou plus sont coplanaires si et seulement s’ils sont linéairement dépendants. Pour montrer que trois vecteurs ou plus sont une combinaison linéaire de deux vecteurs, il suffit que le rang de la matrice formée par tous les vecteurs soit égal à 2.

$rg(A) = 2$

Il est important que vous compreniez bien le concept de dépendance et d’indépendance linéaires , c’est-à-dire lorsque deux vecteurs sont linéairement dépendants ou linéairement indépendants et ce que cela signifie. Si vous n’êtes pas tout à fait clair, vous trouverez dans le lien une explication très détaillée, où, en plus, vous pourrez voir des exemples et des exercices résolus étape par étape.

Si les vecteurs en question sont des vecteurs parallèles , cela signifie qu’ils sont également coplanaires, c’est-à-dire que tous les vecteurs parallèles sont contenus dans le même plan.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Problèmes résolus de vecteurs coplanaires

Exercice 1

Déterminez si les trois vecteurs suivants sont coplanaires :

$\vv{\text{u}} = (3,1,2)$

$\vv{\text{v}} = (2,3,-1)$

$\vv{\text{w}} = (-1,-5,4)$

voir solution

Pour vérifier s’il s’agit de 3 vecteurs coplanaires, il faut calculer le produit mixte entre les trois vecteurs :

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}$

Le produit mixte des trois vecteurs est nul, donc les 3 vecteurs sont coplanaires .

Exercice 2

Déterminez si les trois vecteurs suivants sont coplanaires :

$\vv{\text{u}} = (4,-2,6)$

$\vv{\text{v}} = (-2,1,-3)$

$\vv{\text{w}} = (6,-3,9)$

voir solution

Une façon de vérifier si nous avons affaire à 3 vecteurs coplanaires serait de résoudre le produit mixte entre les trois vecteurs. Cependant, si nous regardons attentivement les composants des vecteurs, nous pouvons voir qu’ils sont proportionnels. Par conséquent, les trois vecteurs sont parallèles les uns aux autres.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Et puisque tous les vecteurs sont parallèles, ce sont effectivement 3 vecteurs coplanaires .

Exercice 3

Déterminez si les quatre vecteurs suivants sont coplanaires :

$\vv{\text{a}} = (2,1,1)$

$\vv{\text{b}} = (1,-1,2)$

$\vv{\text{c}} = (-1,0,-1)$

$\vv{\text{d}} = (3,1,2)$

voir solution

Pour savoir si les quatre vecteurs sont coplanaires, il faut calculer le rang de la matrice composée de tous les vecteurs :

$\displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}$

Dans ce cas, on calcule la portée de ladite matrice par déterminants :

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0$

$\displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0$

$rg(A) = 2$

Le rang de la matrice formée par l’ensemble des vecteurs est équivalent à 2, donc les 4 vecteurs sont coplanaires .

Exercice 4

Calculer la valeur du paramètre

$k$ de sorte que les 4 points suivants sont coplanaires :

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

voir solution

Pour que les quatre points soient coplanaires, les vecteurs déterminés par eux doivent être coplanaires. On calcule donc ces vecteurs :

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

Dont la matrice vectorielle est :

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

Pour que les vecteurs résultants soient coplanaires, le rang de la matrice doit être 2. Et, par conséquent, le déterminant de toute la matrice 3×3 doit être égal à 0 :

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$