Équation vectorielle du plan

Sur cette page, vous trouverez l’équation vectorielle du plan (formule) et des exemples de calcul. De plus, vous pourrez vous entraîner avec des exercices et des problèmes résolus de l’équation vectorielle du plan.

Quelle est l’équation vectorielle d’un plan ?

En géométrie analytique, l’ équation vectorielle d’un plan est une équation qui permet d’exprimer mathématiquement n’importe quel plan. Pour trouver l’équation vectorielle d’un plan, nous n’avons besoin que d’un point et de deux vecteurs linéairement indépendants appartenant à ce plan.

Formule de l’équation vectorielle du plan

Soit un point et deux vecteurs directeurs d’un plan :

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

La formule de l’équation vectorielle d’un plan est :

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Où

$\lambda$ et $\mu$ sont deux scalaires, c’est-à-dire deux nombres réels.

Par conséquent, cela signifie que tout point dans un plan peut être exprimé comme une combinaison linéaire de 1 point et 2 vecteurs.

équation vectorielle du plan xy en ligne

De plus, une condition nécessaire pour que l’équation précédente corresponde à un plan est que les deux vecteurs du plan aient une indépendance linéaire, c’est-à-dire que les deux vecteurs ne puissent pas être parallèles l’un à l’autre.

D’autre part, gardez à l’esprit qu’en dehors de l’équation vectorielle, il existe d’autres façons d’exprimer analytiquement un plan, telles que l’ équation paramétrique du plan et l’ équation implicite du plan . Vous pouvez vérifier en quoi consiste chaque type d’équation dans les liens.

Exemple de comment trouver l’équation vectorielle d’un plan

Une fois que nous avons vu l’explication de la notion d’équation vectorielle du plan, voyons comment elle est calculée à travers un exemple :

Trouver l’équation vectorielle du plan qui passe par le point 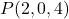$P(2,0,4)$ et contient les vecteurs 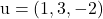$\vv{\text{u}}=(1,3,-2)$ et $\vv{\text{v}}=(5,0,1).$

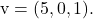
Pour déterminer l’équation vectorielle du plan, il suffit d’appliquer sa formule :

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

Et maintenant, nous substituons le point et chaque vecteur dans l’équation :

$\bm{(x,y,z)=(2,0,4)+\lambda (1,3,-2) + \mu (5,0,1)}$

Comme vous pouvez le voir dans l’exemple, trouver l’équation vectorielle d’un plan est relativement facile. Cependant, les problèmes peuvent devenir un peu compliqués, donc ci-dessous vous avez plusieurs exercices résolus de difficulté différente afin que vous puissiez vous entraîner.

Problèmes résolus de l’équation vectorielle du plan

Exercice 1

Déterminer l’équation vectorielle du plan qui contient le vecteur

$\vv{\text{u}}=(0,-2,3)$ et passe par les deux points suivants : $A(1,3,-1)$ et $B(2,-1,5).$

voir solution

Pour connaître l’équation d’un plan, il faut un point et deux vecteurs et dans ce cas nous n’avons qu’un seul vecteur, il faut donc trouver un autre vecteur directeur du plan. Pour cela, on peut calculer le vecteur qui définit les deux points du plan :

$\vv{AB} = B - A = (2,-1,5) - (1,3,-1) = (1,-4,6)$

Maintenant que nous connaissons déjà deux vecteurs directeurs du plan et un point, nous utilisons donc la formule de l’équation vectorielle du plan :

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

Et nous substituons les deux vecteurs et l’un des deux points du plan dans l’équation :

$\bm{(x,y,z)=(1,3,-1)+\lambda (0,-2,3) + \mu (1,-4,6)}$

Exercice 2

Trouvez l’équation vectorielle du plan qui contient les trois points suivants :

$A(2,-2,1) \qquad B(1,0,4) \qquad C(-1,3,-2)$

voir solution

Pour trouver l’équation vectorielle du plan, nous devons trouver deux vecteurs linéairement indépendants qui se trouvent dans le plan. Et, pour cela, on peut calculer deux vecteurs qui sont définis par les 3 points :

$\vv{AB} = B - A = (1,0,4) - (2,-2,1) = (-1,2,3)$

$\vv{AC} = C - A = (-1,3,-2) - (2,-2,1) = (-3,5,-3)$

Les coordonnées des deux vecteurs trouvés ne sont pas proportionnelles, elles sont donc linéairement indépendantes l’une de l’autre.

Maintenant que nous connaissons déjà deux vecteurs directeurs et un point du plan, nous appliquons donc la formule de l’équation vectorielle du plan :

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

Et nous substituons les deux vecteurs et l’un des trois points du plan dans l’équation :

$\bm{(x,y,z)=(2,-2,1)+\lambda (-1,2,3) + \mu (-3,5,-3)}$

Exercice 3

Calculez 4 points dans l’espace qui appartiennent au plan défini par l’équation vectorielle suivante :

$(x,y,z)=(0,2,1)+\lambda (2,-1,4) + \mu (-1,3,0)$

voir solution

Pour calculer un point sur un plan, il suffit de donner une valeur quelconque aux paramètres

$\lambda$ et $\mu .$ Pourtant:

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(0,2,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(2,1,5)}$

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(-1,5,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(1,4,5)}$

Exercice 4

Trouver l’équation vectorielle du plan qui contient la droite

$r$ et est parallèle à la droite $s.$ étant les lignes :

$\displaystyle r: \ \begin{cases} x=4+2t \\[1.7ex] y=-1+t\\[1.7ex] z=5-4t \end{cases} \qquad \qquad s: \ \frac{x-1}{2} = \frac{y+2}{4}= \frac{z+1}{-3}$

voir solution

Pour trouver l’équation vectorielle du plan, nous devons connaître deux vecteurs directeurs et un point dudit plan. L’instruction nous dit qu’elle contient la ligne

$r$ Par conséquent, nous pouvons prendre le vecteur directeur et un point sur cette ligne pour définir le plan. De plus, l’énoncé nous dit que le plan est parallèle à la droite $s,$ nous pouvons donc également utiliser le vecteur directeur de cette ligne pour l’équation du plan.

le droit

$r$ s’exprime sous la forme d’équations paramétriques, donc les composantes de son vecteur directeur sont les coefficients des termes de paramètre $t:$