Bu makalenin altında, tüm zorluk seviyelerini kapsayan çeşitli çözülmüş yüzde problemleri bulacaksınız. Ek olarak, genellikle yüzdeler kullanılarak incelenen çok çeşitli konuları kapsarlar. Bununla birlikte, sorunları kendi başınıza çözmeye çalışmanızı ve işiniz bittiğinde sonuçlarınızı aynı alıştırmalarda size sunduğumuz sonuçlarla karşılaştırmanızı öneririz. Faaliyetlere başlamadan önce, yüzdelerle ilgili sorunları çözmek için mevcut en iyi yöntemlerden biraz bahsedeceğiz.
Yüzdelerle ilgili problemler nasıl çözülür?
Yüzde problemini çözmek içinMatematik Problemleri İçin Temel Çözme Prosedürünü izlemenizi öneririz. Bu son bağlantıda izlenecek adımların neler olduğunu detaylı olarak anlatacağız, ancak aşağıda yüzdelerin çözümüne yönelik bir özet yapacağız:
- Sorunu anlamak: Çözümün bu ilk aşamasında, sorunu bize hesaplattığı yüzde türüne göre sınıflandırmamız gerekecek. Ana türler genel olarak şunlardır: KDV, artış yüzdeleri, indirim yüzdeleri, denklik yüzdeleri ve diğerleri.
- Bir diyagram yapın: Ne tür bir sorunla karşı karşıya olduğumuzu netleştirdikten sonra, alıştırmanın amacını ve verilerini grafiklemeye geçmeliyiz. Çizim yapmak istemiyorsanız her zaman hesaplamalarda yer alan verileri içeren bir diyagram yazıp bunları birbiriyle ilişkilendirebilirsiniz.
- Hesaplamalarla başlayın: Daha sonra alıştırmayı matematiksel olarak çözmeye başlayabiliriz, önceki bölümlerde alıştırmayı doğru yaptıysanız bu kısım kolaydır. O zamandan beri, sonuca ulaşmak için istediğiniz zaman ne yapmanız gerektiğini çok net bir şekilde bileceksiniz.
- Sonuçlar: Son olarak sonucu ifade etmeliyiz, bu bir cümleyle veya basitçe bizden istenen sayısal değerle olabilir. Ve problemle işimiz bittiğinde onu baştan sona analiz etmemiz ve sonuçlar çıkarmamız şiddetle tavsiye edilir.
Tüm seviyeler için yüzde problemleri
Artık yüzdelerle alıştırmaların nasıl çözüleceğini anlattığımıza göre, bazı alıştırmalarla pratik yapmaya başlayabilirsiniz. Aşağıdaki listede yüzdelerle çalışmaya yeni başlayanlar için alıştırmalardan oldukça karmaşık olanlara kadar tüm sınıf seviyelerine yönelik problemler bulacaksınız. Sahip olduğunuz seviyeye sahip olsanız bile en kolay olanlardan (ilk olanlardan) başlayıp mümkün olduğu kadar yukarı çıkmanızı öneririz.
ilk sorun
Bir okulda 240 öğrenci bulunmaktadır ve bunların 160’ı tüm dersleri geçmiştir. Öğrencilerin yüzde kaçı tüm konuları geçti?
240 öğrenciden tüm konuları geçen 160 öğrencimiz var, yani 240 %100’e, 160 ise %x’e eşittir. X’in değerini bulmak için basit bir üç kural uygulayacağız:
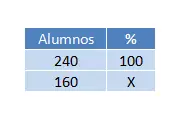
Bu nedenle, işlemin sonucu (160 x 100) ÷ 240 = %66,67 veya toplamın üçte ikisi. Yani çözümü bir cümleyle ifade etmek istiyorsak bunu yüzdeyle belirtebiliriz (açıklamada bize bunu soruyorlar) ya da orantıyla da yapabiliriz.
ikinci problem
Bir otoparkta 150 araba vardır ve bunların %50’si beyaz, %30’u kırmızı ve geri kalanı mavidir. Her renkten kaç araba var?
Toplamda 150 arabamız var ve bunları boya rengine göre 3 farklı gruba ayırmamız gerekiyor. Bu nedenle daha önce olduğu gibi üç hesaplama yapmamız gerekiyor:
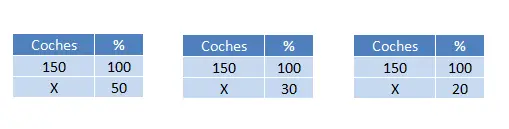
Bu nedenle üç değer elde edeceğiz: (50 x 150) ÷ 100 = 75 araba, (30 x 150) ÷ 100 = 45 araba ve (20 x 150) ÷ 100 = 30 araba. Son olarak, bu sonuçların doğru olup olmadığını kontrol etmek için hepsini toplayabiliriz ve bu bize 150 değerini vermelidir çünkü toplam budur. Bu hesaplama artık çalışmanın bir parçası değil ancak bir kontrol görevi görüyor: 75 + 45 + 30 = 150 araba.
üçüncü sorun
Fiyatı 800€ olan bir televizyon almak istersek ve bize %15 indirim teklif ederlerse, televizyona ne kadar ödeyeceğiz?
Toplam fiyatımız 800€’dur, bu da %15 indirimlidir (bu bir indirim yüzdesidir). O halde üç kuraldan yalnızca birini çözmemiz gerekiyor:
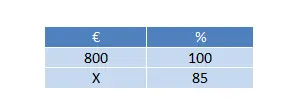
Bu durumda indirim yüzdesine (%100 – %15) = %85’e karşılık gelen değeri hesaplamak gerekir. Bu nedenle son hesaplama şu şekilde kalır: (85 x 800) ÷ 100 = 680€.
dördüncü problem
Bir su depomuzda 250 litre depomuz vardı, ilk gün bu su hacmi toplam kapasitenin %75’ine düşürüldü. Ertesi gün ise kalan kapasite %15 oranında azaldı. İkinci günün sonunda depoda kaç metreküp kaldı?
Bu sorunu çözmek için, ifadede belirlenen sıraya göre iki miktarı hesaplamamız gerekir. Önce 250’nin %75’ini, sonra kalan miktarın %85’ini (%100 – %15) hesaplayacağız.
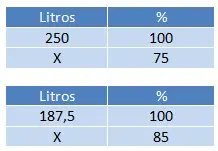
İlk günden kalan miktarı elde etmek için (75 x 250) ÷ 100 = 187,5 litre su çözüyoruz ve ardından (85 x 187,5) ÷ 100 = 159,375 litre su yapıyoruz.
beşinci problem
Biri 135 € ve diğeri 56 € olmak üzere iki ürün için benden %21 KDV alınırsa, ancak ikinci ürün %12 indirimden yararlanır. Her iki ürünü de satın almak için ne kadar ödeyeceğim?
Bu problemde çeşitli hesaplamalar yer almaktadır: İkinci ürünün nihai fiyatını (indirimden sonra) hesaplayarak başlayacağız, ardından iki ürünün KDV’li fiyatını hesaplayacağız ve son olarak iki fiyatı ekleyeceğiz.
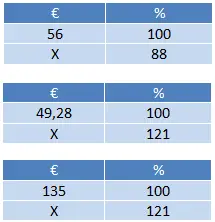
İndirimi uyguladığımızda ikinci ürünün fiyatı (88 x 56) ÷ 100 = 49,28 € olur ve her iki ürüne de KDV uygularız: (121 x 49,28) ÷ 100 = 59,63 € ve (121 x 135) ÷ 100 = € 163.35. Son olarak, 59,63 + 163,35 = 222,98€’yu toplamamız gerekiyor.
son egzersiz
Aşağıdaki yüzdeleri hesaplayın:
- 540’ın %25’i = 135
- 160’ın %32’si = 51,2
- 625’in %46’sı = 287,5
- 873’ün %73’ü = 637,29
Bu alıştırmaları tamamladıysanız ve yüzdelerle ilgili daha fazla problem istiyorsanız bu bağlantıya erişmenizi öneririz. Orada pdf formatında yüzde problemlerini bulacaksınız, bunlar bu yazıda değindiklerimizden çok farklı değil ve yüzde kavramını içselleştirmenizi sağlayacak.