Denklem sistemleri, birden fazla bilinmeyene sahip iki veya daha fazla denklemden oluşan kümelerdir. Dolayısıyla sistemleri çözmek için dört yöntem kullanabiliriz: ikame, eşitleme, indirgeme ve grafik oluşturma. Ancak çözüm prosedürlerini açıklamaya başlamadan önce, çözüm sayısına göre var olan sistem türlerini tanımlayacağız:
- Belirlenmiş uyumlu sistem: Tek bir çözümü vardır ve tek bir noktada kesişen iki doğru ile temsil edilebilir (çözüm budur).
- Belirsiz uyumlu sistem: Çözümleri sonsuzdur ve bunun nedeni aynı noktalarda çakışan iki doğrunun olmasıdır.
- Uyumsuz sistem: Doğruların paralel olması ve dolayısıyla ortak noktalarının olmaması nedeniyle çözümü yoktur.
Doğrusal denklem sistemlerini çözme yöntemleri
Şimdi denklem sistemlerini çözmek için kullanabileceğimiz farklı sistemleri açıklayacağız. Açıklamalarda teoriyi ve bazı örnekleri bulacaksınız, bu sayede açıklanan tüm kavramlar daha net hale gelecektir. Bu makalede yalnızca 2×2 denklem sistemlerinden bahsedeceğimizi unutmayın; bu, yalnızca iki denklemden oluşan sistemlerle ilgileneceğimiz anlamına gelir. Bununla birlikte, açıklamaya başlayalım.
ikame yöntemi
Yerine koyma yöntemi, denklemlerden birindeki bilinmeyenlerden birinin izole edilmesi ve daha sonra elde edilen ifadenin karşıt denklemde yerine konulmasından oluşur. Bu yöntem en çok bilinmeyenlerden en az birinin katsayı değerinin 1’e eşit olduğu durumlarda tavsiye edilir. Dolayısıyla izlenecek adımlar çok basittir:
- Bilinmeyen bir miktarı iki denklemden birinden ayırın.
- İlk denklemden çıkardığımız bilinmeyene eşdeğer ifadeyi diğer denklemde yerine koyun.
- Elde ettiğimiz denklemdeki zıt bilinmeyenleri silin.
- İlk değişkenin değerini aldıktan sonra ikinciyi bulmak için onu kullanmamız gerekir.
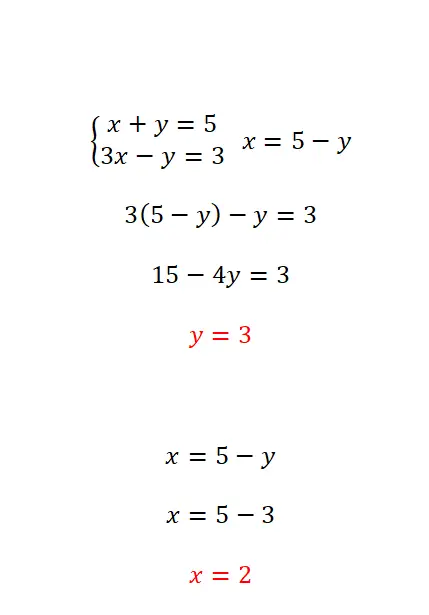
eşitleme yöntemi
Eşleştirme yöntemi, aynı değişkenin iki denklemde izole edilmesi ve ardından elde edilen iki ifadenin eşleştirilmesinden oluşur. Bu yöntem, tüm hesaplamayı kolaylaştırdığı için aynı bilinmeyenin her iki denklemde de kolayca izole edilebildiği durumlarda önerilir. Bu durumda izlemeniz gereken prosedür şu şekildedir:
- İki denklemde seçtiğimiz bilinmeyenleri izole ediyoruz.
- Eşdeğer ifadeleri bu bilinmeyene benzetiyoruz.
- Denklemi normal şekilde çözüyoruz.
- Hesapladığımız değerle diğer bilinmeyeni hesaplıyoruz.
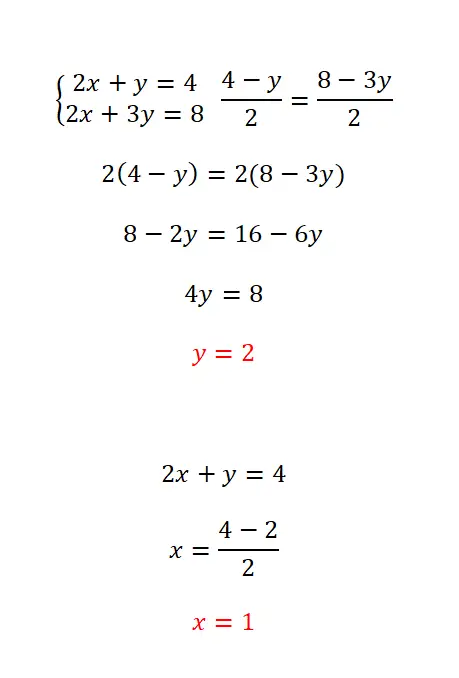
azaltma yöntemi
İndirgeme yöntemi, her iki denklemin iki sayı ile çarpılmasına dayanır ve bu, her iki ifadedeki değişkenlerden birinin farklı işaretiyle aynı katsayıyı elde etmemizi sağlar. Bu yöntem en çok aynı bilinmeyenin tüm denklemlerde aynı katsayıya sahip olduğu veya zıt işaretlerin aynı katsayılara sahip olduğu durumlarda tavsiye edilir. Ve çözüm prosedürü aşağıdaki gibidir:
- İki denklem gerekli sayılarla çarpılır (iki denklemdeki iki değişkenden biri için aynı katsayıyı elde etmeyi mümkün kılan ancak zıt işaretli iki sayı bulmanız gerekir).
- Daha sonra bu bilinmeyeni ilgili katsayılarıyla birlikte ortadan kaldırmak için denklemler çıkarılır veya eklenir.
- Daha sonra kalan denklem çözülür.
- Ve diğer değişkende kaçırdığımız sayısal değeri elde etmek için bu denklemin sonucunu kullanırız.
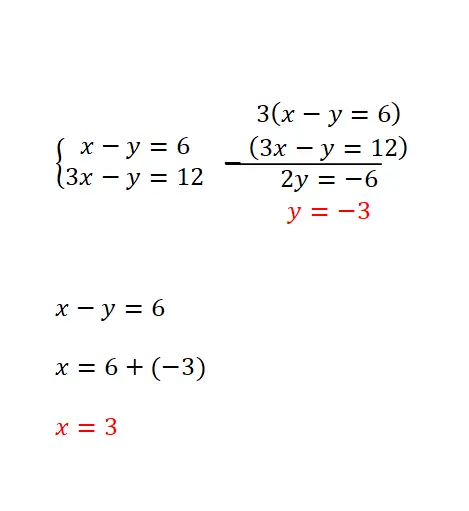
grafik yöntemi
Son olarak, bir denklem sistemini grafiksel gösterim yoluyla çözmeyi seçebiliriz. Bu yöntem diğerlerinden oldukça farklıdır çünkü karmaşık bir matematiksel kısmı yoktur, neredeyse tamamen grafikseldir. Dolayısıyla bilinmeyenlerin değerlerini bilmek için iki denklemi şu doğrunun denklemi biçiminde yapılandırmalıyız: y = mx + b . Bu şekilde gösterimini yapmış olacağız, iki fonksiyon arasındaki kesme noktasının koordinatlarının değerlerini bilinmeyenlerle ilişkilendireceğiz. İşte çalışılmış bir örnek:
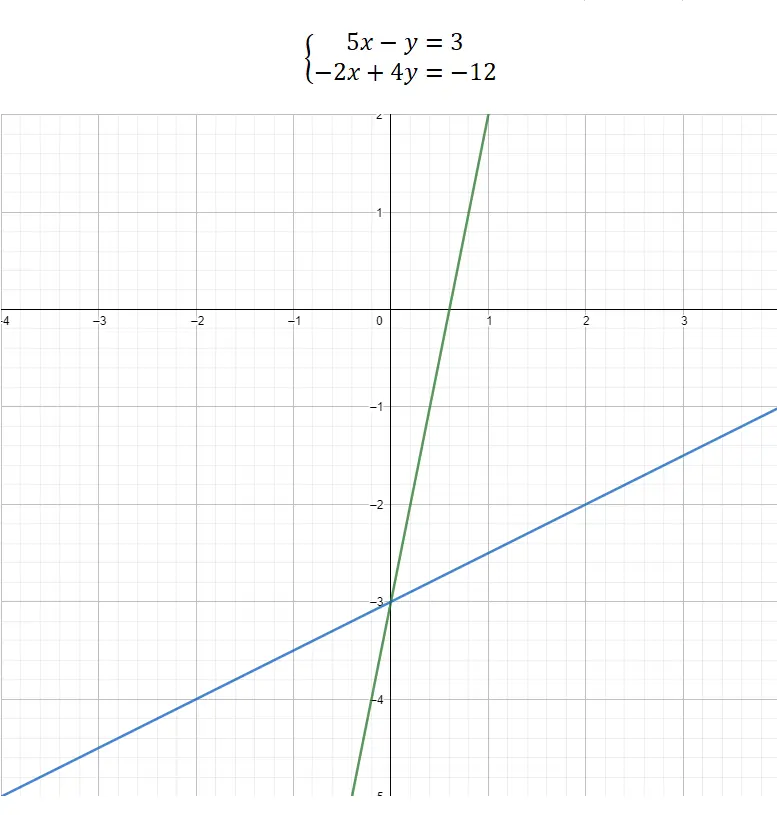
Grafikte görüldüğü gibi iki fonksiyon arasındaki kesme noktası (0, -3)’tür. Dolayısıyla x’in değeri = 0 ve y’nin değeri = -3 olur. Bir denklem sistemi grafiksel olarak bu şekilde çözülür.
İkinci dereceden denklem sistemi nasıl çözülür?
İkinci dereceden denklem sistemlerini çözmek için az önce tartıştığımız yöntemleri kullanabiliriz. Kişisel olarak biz ikame yöntemini tavsiye ediyoruz çünkü bu, tek bilinmeyenli bir denklemi hızlı bir şekilde elde etmemize olanak sağlıyor. Öte yandan indirgeme veya eşitleme yöntemlerini kullanırsak hesaplama oldukça karmaşık hale gelir. Yani, iki değişkenden birini değiştirdiğinizde, yalnızca ortaya çıkan ikinci dereceden denklemi veya ikinci dereceden denklemi çözmeniz gerekir. İşte tüm süreci görebilmeniz için bir örnek:
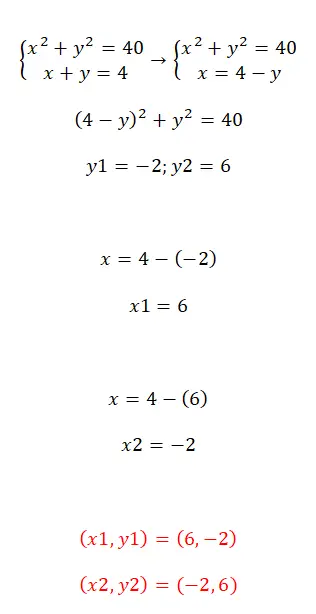
Denklem sistemlerini çözmeye yönelik alıştırmalar
Açıklanan teoriyi uygulayabilmeniz için şimdi size doğrusal ve ikinci dereceden denklem sistemleri üzerine bazı alıştırmalar sunuyoruz. Bu şekilde denklem sistemlerinin hesaplanmasıyla ilgili tüm kavramları daha iyi anlayacaksınız. Sunduğumuz cevaplara bakmadan önce bunları çözmeye çalışmanızı öneririz, böylece alıştırmalardan en iyi şekilde yararlanabilirsiniz:
1. Egzersiz
Bu denklem sistemini ikame yöntemini kullanarak çözün:
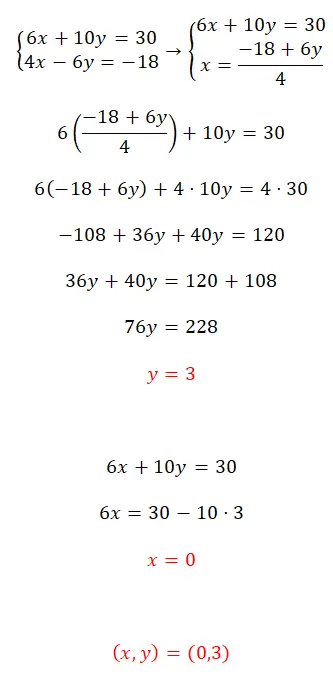
- Bir denklemdeki iki bilinmeyenden birini yalnız bırakarak başlıyoruz.
- Daha sonra karşıt denklemde elde edilen ifadeyi daha önce çözdüğümüz bilinmeyenle değiştiririz.
- Daha sonra karşıt değişkenin sonucunu elde ederiz.
- Daha sonra, ilk bilinmeyenin değerini hesaplamak için ilk keşfedilen değeri iki denklemden birinin yerine koyarız.
- Son olarak iki değişkenin sonucunu ifade ediyoruz.
Alıştırma 2
Bu denklem sistemini ikame yöntemini kullanarak çözün:
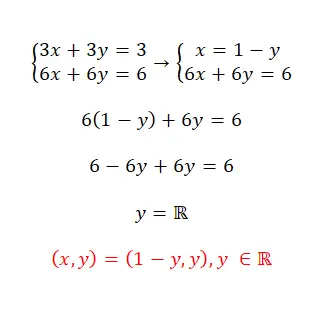
- Bu durumda aynı prosedürü izleyeceğiz: bilinmeyeni izole edin, onu diğer ifadede değiştirin ve ikinci değişkeni izole edin.
- Görebildiğimiz gibi bu belirsiz uyumlu bir sistemdir çünkü sonsuz sayıda çözümü vardır.
Alıştırma 3
Bu denklem sistemini eşitleme yöntemini kullanarak çözün:
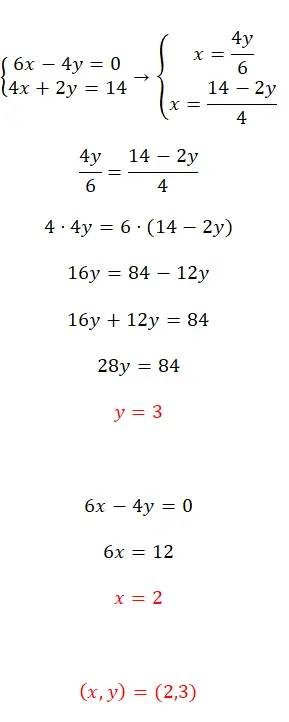
- İlk adım her iki denklemde de aynı değişkeni yalnız bırakmaktır, bu durumda x’i seçtik.
- Daha sonra ortaya çıkan ifadeleri eşleştirip çözmeye başlıyoruz.
- Böylece ilk bilinmeyenin değerini elde etmiş oluyoruz.
- Ve bunu iki orijinal denklemden birinin yerine koyarsak ikinci bilinmeyeni hesaplayabiliriz.
- Son olarak iki değişkenin sonucunu ifade ediyoruz.
Alıştırma 4
Bu denklem sistemini eşitleme yöntemini kullanarak çözün:
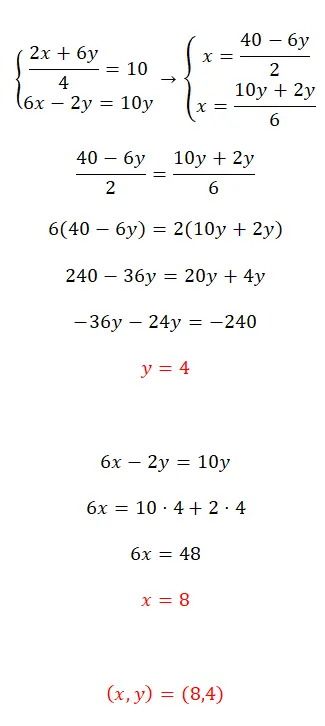
- Öncelikle her iki denklemde de x’i yalnız bırakıyoruz.
- Daha sonra elde ettiğimiz ifadeleri eşleştiriyoruz.
- İlk bilinmeyenin değerini elde ederiz.
- Bu değeri ilk iki denklemden birine yerleştiririz ve ikinci bilinmeyeni hesaplarız.
- Son olarak iki yabancının değerini ifade ediyoruz.
Alıştırma 5
Bu denklem sistemini indirgeme yöntemini kullanarak çözün:
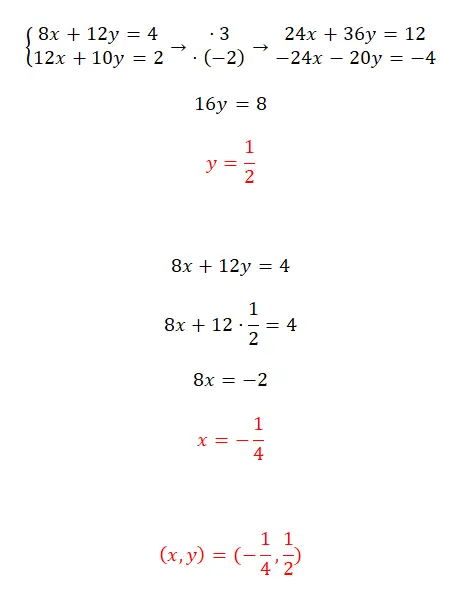
- İki denklemdeki iki değişkenden biri için aynı katsayıyı elde etmeyi mümkün kılan ancak zıt işaretli iki sayı aramalısınız.
- Daha sonra elde ettiğimiz iki ifadeyi toplayarak elde ettiğimiz denklemi basitçe çözün.
- Daha sonra, x’i hesaplamak için y’yi iki orijinal denklemden birinde yerine koyarız.
- Son olarak sistemin sonucunu ifade ediyoruz.
Alıştırma 6
Bu denklem sistemini indirgeme yöntemini kullanarak çözün:
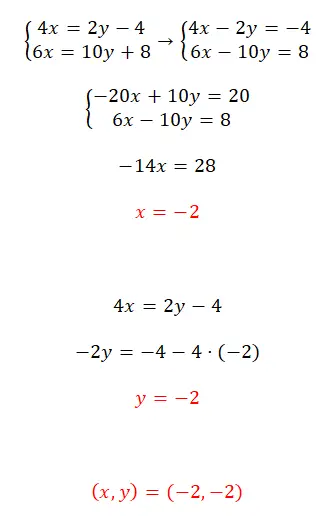
- Denklemleri düzenleyerek başlıyoruz (tüm değişkenleri sola aktarıyoruz).
- Daha sonra ilk denklemi -5 ile çarpıyoruz.
- Elde ettiğimiz denklemi iki denklemi toplayarak çözüyoruz ve x’in değerini elde ediyoruz.
- Y’nin değerini elde etmek için bu bilinen değeri kullanırız.
- Denklem sisteminin sonucunu ifade ediyoruz.
Egzersiz 7
Bu denklem sistemini ikame yöntemini kullanarak çözün:
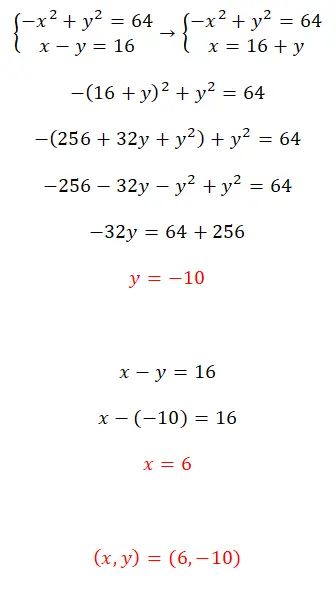
- Bu doğrusal olmayan denklem sistemini çözmek için yerine koyma yöntemini kullanmanızı öneririz.
- Yani x’e eşdeğer bir ifadeyle bir denklem kurarsınız.
- Bilinmeyen y’nin değerini elde edersiniz.
- Daha önce hesapladığınız değerle x’in değerini hesaplarsınız.
- Ve zaten her iki değere de sahipsiniz.
Egzersiz 8
Bu denklem sistemini seçtiğiniz yöntemi kullanarak çözün:
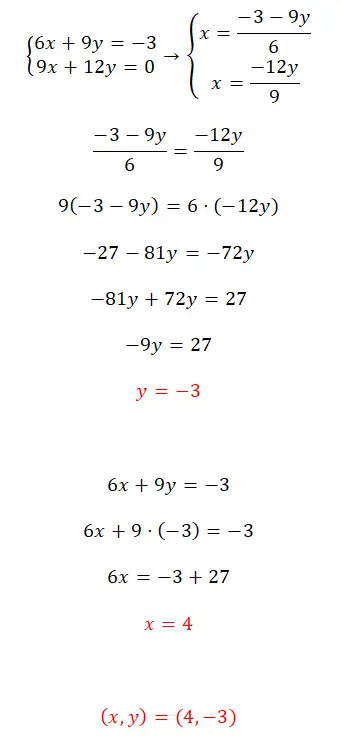
- Bu durumda karşımıza belirlenen uyumlu bir sistem çıkıyor ve bunu eşitleme yöntemini kullanarak çözeceğiz.
- Bu nedenle her iki denklemde de x’i çözüyoruz ve elde edilen iki ifadeyi eşitliyoruz.
- Denklemi çözdükten sonra y değerini elde ederiz.
- Bu değeri x’in değerini bulmak için kullanırız.
- Son olarak sistemin sonucunu ifade ediyoruz.