Yatay asimptot

Bu makalede bir fonksiyonun yatay asimptotlarının ne olduğunu ve nasıl hesaplandığını açıklayacağız. Ek olarak, kavramı tam olarak anlamak için bu tür asimptotların birkaç örneğini bulacaksınız ve ayrıca yatay asimptotlarla ilgili çözümlü alıştırmalar yapabileceksiniz.

Yatay asimptot nedir?

Bir fonksiyonun yatay asimptotu, grafiğinin onu hiç kesmeden sonsuza kadar yaklaştığı yatay bir çizgidir. Bu nedenle yatay asimptot denklemi y=k’dir ; burada k , yatay asimptotun değeridir.

Yani, x sonsuza yaklaşırken fonksiyonun limiti k’ye eşitse k yatay bir asimptottur.

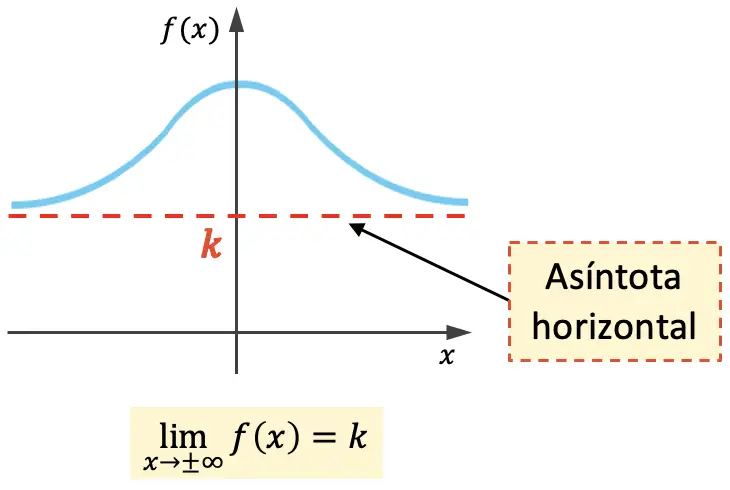
bir fonksiyonun yatay asimptotu

Yukarıdaki fonksiyonun grafiğin her iki tarafında da yatay asimptotu vardır, ancak bir fonksiyonun yalnızca bir tarafında yatay asimptotu olabilir:

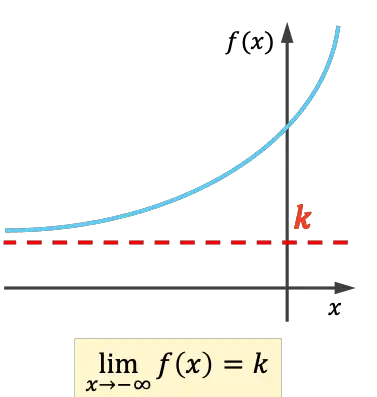
  • En azından sonsuza kadar olan limit gerçek bir sayı veriyorsa, fonksiyonun sol yatay asimptotu vardır.
  • Artı sonsuzun limiti gerçek bir sayı veriyorsa fonksiyonun sağda yatay bir asimptotu vardır.
bir fonksiyonun soldan yatay asimptotu
sağa yatay asimptot

Bir fonksiyonun yatay asimptotu nasıl hesaplanır

Bir fonksiyonun yatay asimptotunu hesaplamak için aşağıdaki adımlar izlenmelidir:

  1. Fonksiyonun sonsuzlara (+∞ ve -∞) limitini hesaplayın.
  2. Sonsuza limit bir gerçek sayı (k) veriyorsa, y=k doğrusu fonksiyonun yatay bir asimptotudur.
  3. Her iki limit de gerçek sayıya karşılık gelmiyorsa, fonksiyonun yatay asimptotu yoktur.

Yatay Asimptot Örneği

Bunun nasıl yapıldığına dair bir örnek görebilirsiniz; aşağıdaki rasyonel fonksiyondaki tüm yatay asimptotları kaldıracağız:

f(x)=\cfrac{x+1}{x-1}

Yatay asimptotları belirlemek için fonksiyonun eksi sonsuzdaki ve artı sonsuzdaki limitini hesaplamak gerekir:

\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}

\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}

➤ Bakınız: sonsuz arasındaki sonsuz belirsizliğin nasıl çözüleceği

Sonsuzdaki iki limit 1 değerini verir, yani y=1 fonksiyonun tek yatay asimptotudur.

Aşağıda grafiksel olarak gösterilen fonksiyon verilmiştir. Gördüğünüz gibi fonksiyon y=1’e çok yaklaşıyor (hem artı sonsuzda hem de eksi sonsuzda), ancak yatay bir asimptot olduğu için ona asla dokunmuyor.

yatay asimptot örneği

Not: Bazı özel durumlarda, fonksiyon yatay asimptotu bir veya daha fazla noktada keser, ancak genel olarak bir fonksiyonun grafiği asimptotlarını hiçbir zaman kesmez.

Öte yandan bu fonksiyonun x=1 noktasında dikey bir asimptotu da vardır. Çünkü grafikten de görebileceğiniz gibi x=1 çizgisine çok yaklaşıyor ama asla o değere ulaşmıyor.

Yatay asimptot problemlerinin çözülmesi

1. Egzersiz

Aşağıdaki kesirli fonksiyonun (varsa) yatay asimptotunu bulun:

\displaystyle f(x)= \frac{4x+3}{2x-1}

Rasyonel fonksiyonun yatay asimptotlarını belirlemek için fonksiyonun sonsuzdaki limitlerini hesaplamak gerekir:

\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}

\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}

Bu durumda, ∞/∞ belirsiz formunun sonucu, pay ve payda aynı mertebeden olduğundan, en yüksek derecedeki x’in katsayılarının bölümüdür.

Fonksiyonun artı sonsuz ve eksi sonsuzdaki limitleri 2 değerini verir, dolayısıyla y=2 yatay bir asimptottur ve fonksiyonun sahip olduğu tek asimptottur.

Alıştırma 2

Aşağıdaki rasyonel fonksiyonun tüm yatay asimptotlarını bir köküyle bulun:

\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}

Fonksiyonun yatay asimptotlarını bulmak için öncelikle pozitif sonsuzdaki limiti hesaplarız:

\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}

Daha sonra fonksiyonun limitini negatif sonsuza çözüyoruz:

\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}

➤ Sonsuzluğun sınırlarının nasıl çözüldüğüne dair şüpheniz varsa, sonsuzluk arasındaki sonsuz belirsizliğin nasıl çözüleceğine ilişkin yukarıdaki bağlantıya göz atmanızı öneririz.

Bu durumda sonsuzdaki limitlerin iki farklı değerini elde ettik. Dolayısıyla fonksiyonun iki yatay asimptotu vardır: y=3 sağdaki fonksiyonun yatay asimptotudur ve diğer taraftan y=-3 soldaki fonksiyonun yatay asimptotudur.

Alıştırma 3

Aşağıdaki parçalı tanımlı fonksiyonun yatay asimptotlarını hesaplayın:

\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.

Fonksiyonun yatay asimptotlarını hesaplamak için formül yoktur, ancak artı ve eksi sonsuzun limitlerini hesaplamanız gerekir.

Böylece en azından sonsuz limiti bulmak için birinci bölümde tanımlanan fonksiyonu alırız:

\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}

Dolayısıyla y=0 doğrusu fonksiyonun solunda yatay bir asimptottur.

Şimdi ikinci bölümde tanımlanan fonksiyonu alarak artı sonsuzdaki limiti hesaplıyoruz:

\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}

Dolayısıyla y=1/2 doğrusu fonksiyonun sağında yatay bir asimptottur.

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top