Yan sınırlar

Bu yazıda bir fonksiyonun yanal limitinin ne olduğunu (örneklerle) açıklıyoruz. Ayrıca size bir fonksiyonun sol ve sağ yan limitlerini hem grafik hem de sayısal olarak nasıl hesaplayacağınızı öğretiyoruz. Ayrıca yanal limitlerin adım adım çözüldüğü egzersizlerle antrenman yapabileceksiniz.

Yanal sınırlar nelerdir?

Bir fonksiyonun bir noktadaki yanal sınırları, fonksiyonun o nokta etrafındaki davranışını inceler. Dikkate alınan noktanın sırasıyla solunda ve sağında fonksiyonun değerini analiz eden sol yanal limit ve sağ yanal limit bulunmaktadır.

Sol ve sağ yanal sınırlar

Yan sınırların tanımında gördüğümüz gibi iki tür vardır: sol yan sınırlar ve sağ yan sınırlar.

Limitin analiz edildiği noktada fonksiyonun sol limiti eksi işaretiyle, sağ limiti ise artı işaretiyle gösterilir.

Yanal sınırların anlamını daha iyi anlamak için aşağıdaki örneğe bakın:

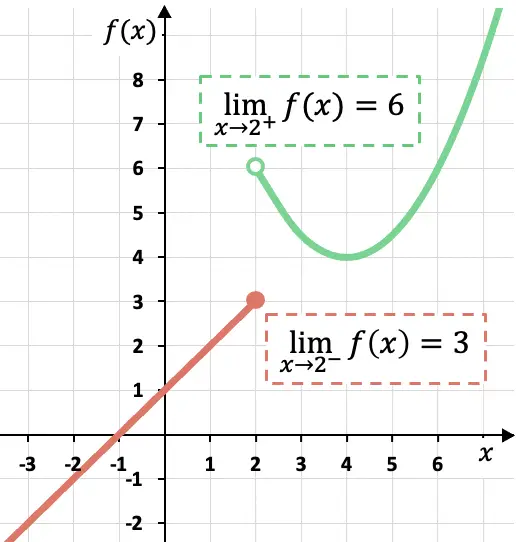
Bu parçalı fonksiyonun grafiksel gösteriminde görebileceğiniz gibi, yanal sınırlar hesaplandıkları tarafa bağlıdır.

Bu durumda x, 2’ye soldan yaklaştıkça fonksiyon 3’e yaklaşmaktadır, çünkü x , x=2’ye solundan yaklaştıkça fonksiyon 3’e yakın değerler almaktadır.

Öte yandan fonksiyonun x=2 noktasındaki doğruya göre yanal limiti 6 değerindedir. Çünkü x=2 noktasına onun doğrusuyla yaklaşırsak fonksiyon f(x)= değerine giderek daha yakın değerler alır. 6.

Öte yandan yanal limitlerin sıradan limitlerle aynı özelliklere sahip olduğunu bilmelisiniz. Aşağıdaki bağlantıda sınır özelliklerinin ne olduğunu görebilirsiniz:

➤ Bakınız: sınır özellikleri

eşit yanal sınırlar

Az önce bir fonksiyonun yan limitlerinin farklı olduğu bir örnek gördük ama… eğer yan limitler aynıysa ne olur?

Bir fonksiyonun bir noktada her iki yanal limiti de varsa ve eşitse , o noktada fonksiyonun limiti de vardır ve limitin sonucu yanal limitlerin değeridir.

Başka bir deyişle, bir fonksiyonun limitinin bir noktada var olabilmesi için aşağıdaki koşulun sağlanması gerekir:

Dolayısıyla bir fonksiyonun bir noktadaki yanal limitleri farklı ise fonksiyonun o noktadaki limiti mevcut değildir.

Ayrıca bir fonksiyonun bir noktadaki limitinin mevcut olması, onun bir noktada sürekli fonksiyon olabilmesinin temel koşuludur.

Yanal limit kavramını anlamayı tamamlamak için bir örnek çözelim:

Grafiksel olarak temsil edilen fonksiyonun x=-2 noktasındaki yanal sınırları çakışmaktadır, çünkü fonksiyonun değeri x=-2’ye soldan da sağdan da yaklaşsak 3’e doğru yönelmektedir. Dolayısıyla fonksiyonun x=-2’deki limiti 3’e eşittir.

Öte yandan, x=4 noktasında yanal sınırlar farklıdır, çünkü fonksiyon soldan f(x)=3’e, sağdan f(x)=2’ye yaklaşmaktadır. Bu nedenle fonksiyonun bu noktada limiti mevcut değildir.

Yanal sınırların hesaplanması

Yanal sınırların tanımı verildiğinde, aşağıdaki örneği çözerek bunların sayısal olarak nasıl hesaplandığını göreceğiz:

Limiti her zamanki gibi hesaplarsak, bir reel sayının belirsizliğini 0’a bölerek elde ederiz:

Ancak yanal limitleri hesaplarken herhangi bir belirsizlikle karşılaşmıyoruz.

Fonksiyonun x=2 noktasında soldan yanal limitini hesaplamak için x=2’den küçük ancak ona çok yakın bir sayı almanız gerekir, örneğin x=1,999.

Bu durumda payda, değeri çok küçük olan ancak sıfır bile olmayan negatif bir sayı olacaktır ve genellikle sıfır ve önünde bir eksi işaretiyle temsil edilir:

Bu nedenle, yan sınırın sonucu eksi sonsuzdur, çünkü herhangi bir sayının 0’a bölünmesi sonsuzluğu verir ve pozitifin negatife bölünmesi negatif verir:

Fonksiyonun soldan x=2’ye yakın değerlere sahip görüntülerini hesaplayarak fonksiyonun eksi sonsuza yaklaştığını doğrulayabiliriz.

Aynı şekilde sağdaki x=2 noktasında fonksiyonun limitini bulmak için de aynı mantığı uygulayabiliriz: 2’den büyük ama çok yakın bir değer alıyoruz, örneğin 2001 gibi.

Aynı şekilde fonksiyonun sağdan x=2’ye yakın ve yakın değerlerdeki görüntülerini hesaplayarak fonksiyonun sonsuza doğru yöneldiğini doğrulayabiliriz.

Aşağıdaki grafikte analiz edilen fonksiyonu temsil ettiğini görebilirsiniz. Gördüğünüz gibi fonksiyonun soldaki x=2 noktasındaki yanal limiti eksi sonsuz, sağdaki x=2 noktasındaki fonksiyonun yanal limiti ise artı sonsuzdur.

Yan sınır sorunları düzeltildi

1. Egzersiz

Aşağıdaki parçalı tanımlı fonksiyonun tanımının değiştiği noktalardaki (x=-2 ve x=4) yanal limitlerini bulun.

Yanal sınırlar x=-2 noktasında çakışmaz, solda fonksiyon f(x)=5’e doğru yönelir ve sağda ise fonksiyon sabittir ve 3 değerindedir.

x 4’e yaklaştıkça yan sınırlar da farklıdır. Parçalı fonksiyon soldan 3’e, sağdan -2’ye yaklaşır.

Alıştırma 2

Aşağıdaki parçalı fonksiyonun x’i 3’e yaklaşırken limitin var olup olmadığını ve eğer öyleyse değerinin ne olduğunu belirleyin.

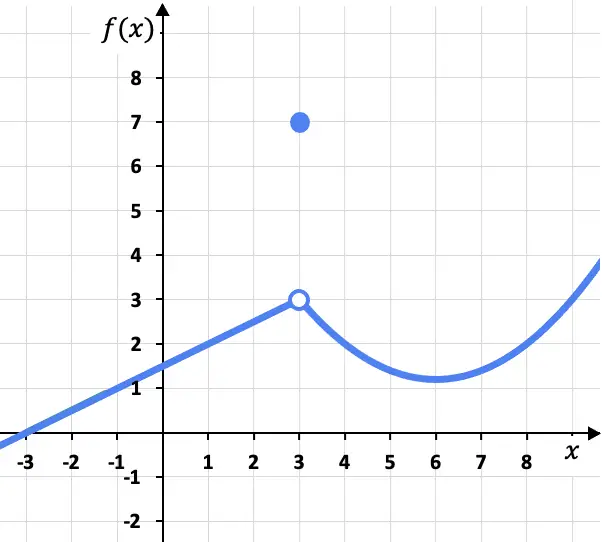
Bu problemde x=3 noktasında soldan ve sağdan yanal limitler aynıdır, çünkü fonksiyon ister soldan ister sağdan yaklaşılsın aynı değere (f(x)=3) doğru yönelir. . sağ tarafı:

Dolayısıyla limitin matematiksel tanımına göre fonksiyonun x’in 3’e yöneldiği andaki limiti 3’e eşittir çünkü aynı noktadaki iki yanal limit bu değerde çakışmaktadır:

Fonksiyonun x=3 noktasındaki limiti 3 olmasına rağmen bu noktadaki fonksiyonun 3 değil f(3)=7 olduğunu dikkate almak gerekir. Daha sonra göreceğimiz gibi bu, fonksiyonun x=3’te sürekli olmadığı, aksine kaçınılabilir bir süreksizliğe sahip olduğu anlamına gelir.

Alıştırma 3

Aşağıdaki rasyonel fonksiyonun x=4 noktasındaki yanal limitlerini hesaplayın.

X soldan 4’e doğru yöneldiğinde limiti hesaplamak için 4’ten küçük ama ona çok yakın bir değer alırız, örneğin 3,999:

Yani x 4’e soldan yaklaşırken yanal limit artı sonsuzdur.

Ve x sağdan 4’e doğru yöneldiğinde limiti çözmek için fonksiyonu 4’ten büyük ancak ona çok yakın bir değerde, örneğin 4,001 olarak değerlendiririz:

Yani x 4’e sağdan yaklaşırken yanal limit eksi sonsuzdur.

Alıştırma 4

x=2 noktasında tanımlanan aşağıdaki parçalı fonksiyonun limitini (varsa) bulun: