Uzayda iki çizginin göreceli konumu

Burada uzaydaki (R3’te) iki çizginin tüm göreceli konumlarını bulacaksınız. Ek olarak, iki olası yöntem kullanılarak iki çizgi arasındaki göreceli konumun nasıl bulunacağı açıklanmaktadır: aralıklara göre veya bir noktadan ve her çizginin bir vektöründen. Hatta adım adım çözülen örnekleri ve alıştırmaları görebileceksiniz.

Uzayda iki çizginin göreceli konumları nelerdir?

Analitik geometride, üç boyutlu bir uzayda (R3’te) çalışırken, iki çizgi arasında 4 olası göreceli konum vardır: iki çizgi birleşen çizgiler , paralel çizgiler , kesen çizgiler veya kesen çizgiler olabilir.

Paralel çizgiler

İki doğru aynı yöne sahip ancak ortak noktaları yoksa paraleldir. Ayrıca paralel çizgiler her zaman birbirlerinden aynı uzaklıkta olur.

çakışan çizgiler

İki doğru aynı yöne sahipse ve ayrıca tüm noktaları ortaksa çakışır.

Kesişen çizgiler

Kesişen iki doğrunun yönleri farklıdır ancak bir noktada birbirine değmektedir.

Kavşak çizgileri

Kesişen iki doğrunun yönleri farklıdır ve hiçbir noktada kesişmezler. Bu nedenle çapraz iki doğru aynı düzlemde değildir. Örneğin çizginin üzerindeki grafiksel gösterimde

$s$

her zaman çizginin ilerisindedir

$r$

Böylece birbirlerine asla dokunmayacaklar.

İki doğru arasındaki göreceli konumun ne olduğunu bilmenin 2 yolu vardır, çünkü bunlar iki doğrunun denklemlerinin nasıl ifade edildiğine bağlıdır:

Çizgiler vektör, parametrik veya sürekli denklem biçimindeyse, bir noktadan ve her çizginin bir vektöründen göreli konumu hesaplamak en iyisidir (bu yöntemin açıklaması aşağıda verilmiştir).
Öte yandan, çizgiler örtülü (veya genel) denklemler biçiminde tanımlanmışsa, iki matrisin rütbesini hesaplayarak iki çizgi arasındaki göreceli konumu bilmek daha kolaydır (aşağıdaki açıklamaya bakın).

Bir noktadan ve bir vektörden iki doğrunun göreceli konumunu belirleme

Her bir doğrunun bir noktası ve bir vektörü bulunan iki doğru arasında hangi göreceli konumun olduğunu bulabilirsiniz. Bu yöntem, doğruların bir vektör denklemi, parametrik denklemler veya sürekli bir denklem biçiminde tanımlandığı durumlarda kullanılması uygundur.

Böylece, yön vektörü ve iki çizginin her birindeki herhangi bir nokta şöyle olsun:

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

Dolayısıyla iki çizginin göreceli konumunu bulmak için aşağıdaki prosedürü izlememiz gerekir:

‣ Yapmamız gereken ilk şey iki doğrunun vektörlerinin orantılı olup olmadığına bakmak ve duruma göre aşağıdakileri yapıyoruz:

İki vektör orantılıysa çizgiler paralel veya çakışık olabilir. Bu nedenle bir doğrunun noktasının diğer doğrunun denklemini sağlayıp sağlamadığını kontrol etmeliyiz:
- Bir doğrunun noktası diğer doğrunun denklemini sağlıyorsa iki doğru çakışıyor demektir.
- Aksi takdirde iki doğrunun paralel olduğu anlamına gelir.
İki vektör orantılı değilse çizgiler kesişiyor veya kesişiyor olabilir. Bu durumda aşağıdaki 3×3 determinantını çözmemiz gerekir:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- Önceki determinant sıfıra eşitse, iki doğru bir noktada kesişir (kesişirler).
- Önceki determinant sıfırdan farklıysa iki doğru kesişir.

Aşağıdaki grafik tüm prosedürü özetlemektedir:

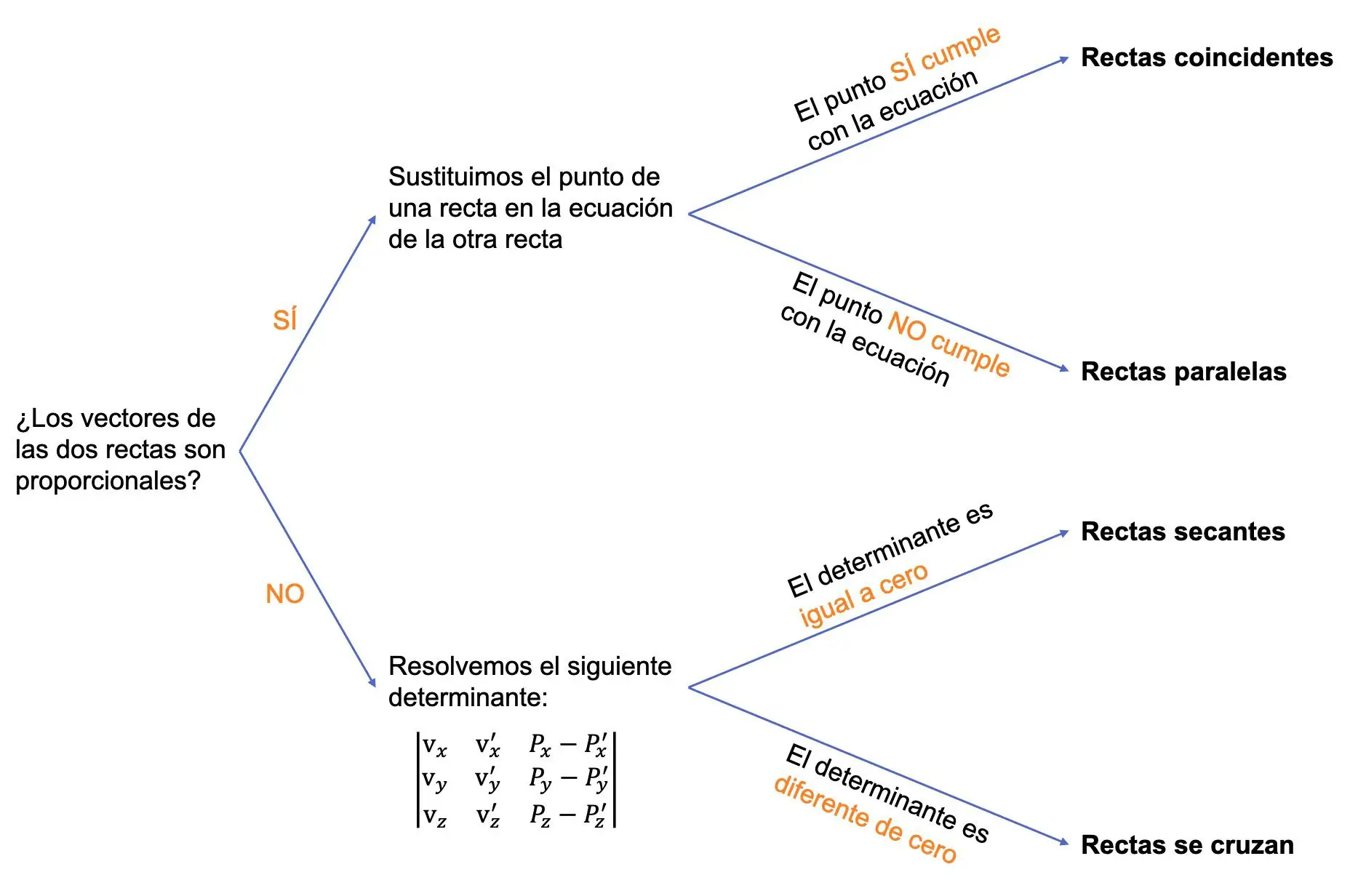
İki çizgi arasındaki göreceli konumu belirleme örneği

Önceki prosedür biraz karmaşık görünebilir, ancak bunun tam tersi olduğunu görebilmeniz için örnek olarak bir sorunu çözeceğiz:

Aşağıdaki iki çizgi arasındaki göreceli konumu belirleyin:

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

İki çizgi bir vektör denklemi olarak ifade edilir ve her çizginin yön vektörü şu şekildedir:

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

Ve her çizginin geçtiği nokta:

$R(2,0,1)\qquad \qquad S(1,-3,1)$

Bir noktayı ve her doğrunun yön vektörünü öğrendikten sonra yukarıda görülen yöntemi uygularız. Öncelikle vektörlerin koordinatlarının orantılı olup olmadığını kontrol etmeliyiz:

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

İki vektör birbiriyle orantılı olmadığından çizgiler yalnızca birbirine değebilir veya kesişebilir. Bu nedenle şimdi yön vektörü ve her doğru üzerindeki bir noktanın oluşturduğu aşağıdaki determinantı çözmemiz gerekiyor:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Değerleri formülde değiştiririz:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

Ve determinantı hesaplıyoruz, bunun için herhangi bir yöntemi kullanabilirsiniz (Sarrus kuralı, tamamlayıcılar veya kofaktörler yöntemi, vb.):

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

Belirlemenin sonucu sıfır olsaydı, bu, çizgilerin kesiştiği (birbirine değdiği) anlamına gelirdi. Ancak determinant 0’dan farklı olduğundan doğrular kesişir .

İki satırın göreceli konumunu satırlara göre bulun

İki satırın göreceli konumunu bulmanın başka bir yolu da, daha sonra göreceğimiz gibi, iki somut matrisin derecelerini hesaplamaktır. Bu yöntem, iki doğru örtülü (veya genel) denklem biçiminde olduğunda çok kullanışlıdır.

Dolayısıyla, üç boyutlu bir uzayda (R3’te) örtülü (veya genel) denklemleriyle ifade edilen iki çizgimiz varsa:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

A, iki doğrunun katsayılarından oluşan matris olsun:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

Ve iki çizginin tüm parametrelerinin oluşturduğu matris olan genişletilmiş A’ matrisi verildiğinde:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Daha sonra, iki satırın göreceli konumu, aşağıdaki tabloya göre önceki iki matrisin aralığına göre belirlenebilir:

iki satırın satırlara göre göreceli konumları

Bu nedenle, iki satır arasındaki göreceli konumu bulmak için iki matrisin sıralarını hesaplamamız gerekecek ve her bir matrisin sırasına bağlı olarak iki durumdan biri olacaktır.

Bu teorem, Rouché-Frobenius teoremi (doğrusal denklem sistemlerini çözmek için kullanılan bir yöntem) kullanılarak kanıtlanabilir, ancak bu sayfada ispatı yapmayacağız çünkü oldukça hantaldır ve fazla bir şey katmaz.

İki çizginin göreceli konumunun aralıklara göre nasıl bulunacağına ilişkin örnek

İki satır arasındaki göreceli konumlara ilişkin teoriyi satır satır gördükten sonra, bir örnek üzerinden bunun nasıl uygulamaya konulduğunu görelim:

Aşağıdaki iki çizginin göreceli konumunu bulun:

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

İki çizgi genel (veya örtülü) denklemler biçimindedir, dolayısıyla iki çizgi arasındaki göreceli konumu bulmak için sıralar yöntemini kullanacağız. Bu nedenle A matrisini ve genişletilmiş A’ matrisini çizgilerin katsayılarıyla oluşturuyoruz:

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

Her iki matrisi de elde ettiğimizde, her birinin sıralamasını hesaplamamız gerekir. Öncelikle A matrisinin rütbesini determinantlara göre hesaplıyoruz:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

Matris A, sıfır olmayan bir 3×3 alt matrisinin determinantını içerir, dolayısıyla A matrisinin derecesi 3’tür .

Şimdi genişletilmiş A’ matrisinin kapsamını hesaplıyoruz. A’ matrisi her zaman en azından A matrisinin mertebesinde olacaktır, bu durumda bu değer 3’tür, dolayısıyla onun mertebe 4’te mi yoksa mertebe 3’te mi olduğunu kontrol etmek yeterlidir. Bunu yapmak için determinantı çözeriz. 4× matris 4’ün eklemelerle (veya kofaktörlerle):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

Genişletilmiş matrisin tamamının determinantı sıfırdır, dolayısıyla A’ matrisi de 3. sıradadır .

Yani A matrisi ve A’ matrisi rütbe 3’tür, dolayısıyla iki doğru kesişir . Yani aralarında tek bir kesişim noktası vardır.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

Yukarıda, A ve A’ matrislerinin aralıklarına göre iki çizgi arasındaki göreceli konumların tüm olası durumlarını özetleyen bir tablonuzun bulunduğunu unutmayın.

Uzayda iki çizgi arasındaki göreceli konum problemleri çözüldü

1. Egzersiz

Aşağıdaki iki çizgi arasındaki göreceli konumu bulun:

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

Çözüme bakın

Her iki çizgi de bir vektör denklemi olarak ifade edildiğinden, iki çizgi arasındaki göreceli konumu, her çizginin bir noktasından ve bir vektör yönteminden bulacağız.

Her çizginin yön vektörü:

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

Ve her doğruya ait olan bir nokta:

$R(3,4,0)\qquad \qquad S(1,-2,2)$

Bu nedenle, prosedürü uygulamak için öncelikle yön vektörlerinin bileşenlerinin orantılı olup olmadığını kontrol etmek gerekir:

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

İki vektör birbiriyle orantılı olmadığından çizgiler yalnızca kesişebilir veya kesişebilir. Bu nedenle şimdi yön vektörü ve her doğru üzerindeki bir noktadan oluşan aşağıdaki determinantı çözmemiz gerekiyor:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Değerleri formülde değiştiririz:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

Ve determinantı hesaplıyoruz:

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

Belirleyicinin sonucu 0’a eşdeğer olduğundan çizgiler kesişir .

Alıştırma 2

Aşağıdaki iki çizginin göreceli konumunu hesaplayın:

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

Çözüme bakın

İlk çizgi parametrik denklemler biçiminde, ikinci çizgi ise sürekli bir denklem biçimindedir; bununla her çizginin tek nokta vektör yönteminden iki çizgi arasındaki göreceli konumu belirleyeceğiz.

Sağdaki yön vektörünün koordinatları

$r$

parametrenin önündeki katsayılardır

$t,$

ve çizginin yön vektörünün koordinatları

$s$

paydaların sayıları şunlardır:

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

Ve her doğruya ait olan bir nokta:

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

Bu nedenle, prosedürü uygulamak için öncelikle yön vektörlerinin bileşenlerinin orantılı olup olmadığını kontrol etmek gerekir:

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

İki vektör birbiriyle orantılı olduğundan çizgiler yalnızca paralel veya çakışık olabilir. Bu şüpheyi ortadan kaldırmak için noktayı çizgi üzerinde değiştirmek gerekir.

$r$

doğrunun denkleminde

$s$

(veya tam tersi) söz konusu denklemi karşılayıp karşılamadığını görmek için:

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

Noktayı doğru üzerinde değiştirerek bir eşitlik elde ederiz, böylece bir doğrunun noktası diğer doğrunun denklemini karşılar ve ayrıca yön vektörleri orantılıdır. Bu nedenle iki çizgi çakışmaktadır.

Alıştırma 3

Aşağıdaki iki çizginin göreceli konumunu bulun:

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

Çözüme bakın

İki çizgi genel (veya ima edilen) denklem biçimindedir, bu nedenle iki çizgi arasındaki göreceli konumu bulmak için sıralama yöntemini kullanacağız. Bu nedenle A matrisini ve genişletilmiş A’ matrisini çizgilerin katsayılarıyla yaparız:

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

Her iki matrisi de elde ettiğimizde, her birinin sıralamasını hesaplamamız gerekir. Öncelikle A matrisinin rütbesini determinantlara göre hesaplıyoruz:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

A matrisinin tüm 3×3 determinantları sıfırdır, ancak matrisin içinde sıfırdan farklı bir 2×2 determinantı vardır, dolayısıyla A matrisinin derecesi 2’dir .

Şimdi genişletilmiş A’ matrisinin kapsamını hesaplıyoruz. A’ matrisi her zaman en azından A matrisinin aralığı olacaktır, bu durumda bu 2’dir, bu nedenle birbirini götürmeyen 3×3 determinantına sahip olup olmadığını ve ayrıca matrisin determinantının ne kadar olduğunu kontrol etmek gerekir. matrisin tamamı:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

Genişletilmiş A’ matrisi aslında 3×3 sıfır olmayan alt belirleyiciler içerir ve ayrıca tüm genişletilmiş matrisin determinantı 0’a eşittir, dolayısıyla A’ matrisinin derecesi 3’tür .

Yani A matrisi rütbe 2’de ve A’ matrisi rütbe 3’tedir, yani iki çizgi paraleldir . Yani aralarında hiçbir ortak nokta yok.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

Yöntemin (yukarıdaki) açıklamasında, A ve A’ matrislerinin sıralarına göre iki çizgi arasındaki tüm olası göreceli konum durumlarını özetleyen bir tablonuzun bulunduğunu unutmayın.

Alıştırma 4

Aşağıdaki iki çizginin göreceli konumunu bulun:

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

Çözüme bakın

Bu durumda, iki çizgi Kartezyen (veya örtülü) denklem formundadır, dolayısıyla iki çizgi arasındaki göreceli konumu bulmak için sıralama yöntemini kullanacağız. Bu nedenle A matrisini ve genişletilmiş A’ matrisini çizgilerin katsayılarıyla oluşturuyoruz:

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

İki matrisi öğrendikten sonra her birinin sıralamasını hesaplamamız gerekir. İlk önce A matrisinin rütbesini determinantlara göre hesaplayacağız:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

A matrisi, determinantı sıfır olmayan 3×3’lük bir alt matris içerir, dolayısıyla A matrisinin derecesi 3’tür .

Şimdi genişletilmiş A’ matrisinin kapsamını hesaplıyoruz. A’ matrisi her zaman en azından A matrisinin mertebesinde olacaktır, bu durumda bu değer 3’tür, dolayısıyla onun mertebe 4’te mi yoksa mertebe 3’te mi olduğunu kontrol etmek yeterlidir. Bunu yapmak için, matrisin determinantını çözüyoruz. eklemelere (veya kofaktörlere) göre 4 × 4 matris kümesi:

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$

$\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9$

$\displaystyle =-100-21+18$

$\displaystyle =-103\bm{\neq0}$

$rg(A')=4$

Genişletilmiş matrisin tamamının determinantı sıfır değildir, dolayısıyla A’ matrisinin derecesi 4’tür .

Böylece A matrisi rütbe 3’te ve tam tersine A’ matrisi rütbe 4’te olduğundan iki doğru bir noktada kesişir .

$\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}$

Prosedürün (yukarıdaki) açıklamasında, A ve A’ matrislerinin sıralarına göre iki çizgi arasındaki tüm olası göreceli konum durumlarının bulunduğu bir tablonuz olduğunu unutmayın.

Uzayda iki çizginin göreceli konumları nelerdir?

Bir noktadan ve bir vektörden iki doğrunun göreceli konumunu belirleme

İki çizgi arasındaki göreceli konumu belirleme örneği

İki satırın göreceli konumunu satırlara göre bulun

İki çizginin göreceli konumunun aralıklara göre nasıl bulunacağına ilişkin örnek

Uzayda iki çizgi arasındaki göreceli konum problemleri çözüldü

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et