▷ Uzayda analitik geometri ile ilgili her şey ✅

Bu sayfada uzayda analitik geometri (ve formüller) ile ilgili her şeyin açıklamasını bulacaksınız: doğru ve düzlem denklemleri, düzlemler ve doğrular arasındaki göreceli konumlar, uzayda mesafelerin ve açıların nasıl hesaplandığı,…

Uzayda geometri nedir?

Uzay geometrisi, üç boyutlu (3D) geometrik şekillerin, yani uzayda bir yer kaplayanların incelenmesinden sorumlu olan geometri dalıdır. Koni, küp, piramit, küre, silindir, prizmalar, çokyüzlüler vb. gibi.

Ancak bu sayfada uzay geometrisinin noktaların, çizgilerin, düzlemlerin, iki geometrik şekil arasındaki mesafelerin, oluşturdukları açının, farklı geometriler arasındaki kesişme noktalarının analizine odaklanan kısmı olan uzayda analitik geometriye odaklanacağız. rakamlar. unsurlar vb.

Uzaydaki çizginin denklemleri

Bir çizginin matematiksel tanımının, eğriler veya açılar olmadan aynı yönde temsil edilen ardışık noktalar kümesi olduğunu hatırlayın.

Dolayısıyla, herhangi bir doğruyu üç boyutlu uzayda (R3’te) matematiksel olarak ifade etmek için doğrunun denklemlerini kullanırız ve bunları bulmak için yalnızca doğruya ait bir noktaya ve söz konusu doğrunun yön vektörüne ihtiyacımız vardır.

Yalnızca bu iki geometrik öğeyle, aşağıdaki gibi olan çizginin tüm farklı denklemlerini kesinlikle bulabilirsiniz:

Doğrunun denklemleri vektör denklemi , parametrik denklemler , sürekli denklem ve örtülü (veya genel) denklemdir .

Aşağıda doğrunun farklı denklem türlerinin bir açıklaması bulunmaktadır.

Uzayda çizginin vektör denklemi

Evet

$\vv{\text{v}}$

çizginin yön vektörüdür ve

$P$

sağa ait bir nokta:

$\vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z) \qquad P(P_x,P_y,P_z)$

Doğrunun vektör denkleminin formülü şöyledir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=(P_x,P_y,P_z)+t\cdot (\text{v}_x,\text{v}_y,\text{v}_z) \end{empheq}$

Uzaydaki çizginin parametrik denklemleri

Bir doğrunun parametrik denkleminin formülünü, bileşeni bileşene eşitleyerek vektör denkleminden elde edebiliriz:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_x+t\cdot\text{v}_x \\[1.7ex] y=P_y+t\cdot\text{v}_y \\[1.7ex] z=P_z+t\cdot\text{v}_z\end{cases} \end{empheq}$

Uzayda çizginin sürekli denklemi

Doğrunun sürekli denkleminin formülü şöyledir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_x}{\text{v}_x}=\cfrac{y-P_y}{\text{v}_y}= \cfrac{z-P_z}{\text{v}_z} \end{empheq}$

Bu tür doğru denklemleri parametrik denklemlerden de elde edilebilir, sürekli denklem sayfamızda gösterimini görebilir, ayrıca sağdan denklemlerin çözülmüş alıştırmalarıyla örnekleri görebilir ve pratik yapabilirsiniz.

Uzaydaki çizginin genel (veya örtülü) denklemleri

Son olarak doğrunun sürekli denkleminin kesirlerini ikiyle ikiyle çarparak doğrunun genel (veya örtülü) denklemlerini elde ederiz:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} A_1x+B_1y+C_1z+D_1=0 \\[1.7ex] A_2x+B_2y+C_2z+D_2=0\end{cases} \end{empheq}$

Doğrunun bu tür denklemine Kartezyen denklem de denir.

Az önce doğrunun en alakalı 4 denklemini gördük (vektör, parametrik, sürekli ve genel), ancak biraz özel bir denklem daha var ve bu nedenle onu açıklamak tam bir sayfa alıyor. Bu kanonik denklemdir , bu bağlantıda onun tüm açıklamasını, neden bu kadar özel olduğunu ve onu diğerlerinden farklı kılan şeyin ne olduğunu görebilirsiniz.

Uzayda düzlem denklemleri

Analitik geometride bir düzlemin denklemi , herhangi bir düzlemin analitik olarak ifade edilmesini sağlayan bir denklemdir. Yani bir düzlemin denklemini bulmak için yalnızca bir noktaya ve söz konusu düzleme ait iki doğrusal bağımsız vektöre ihtiyacınız vardır.

Dolayısıyla, düzlemin tüm denklem türleri şunlardır: vektör denklemi , parametrik denklemler , örtülü (veya genel) denklem ve düzlemin kanonik (veya segmental) denklemi .

Daha sonra planın tüm denklemlerinin açıklamasını ve formülünü göreceğiz.

Düzlemin vektör denklemi

Bir düzlemin bir nokta ve iki yön vektörü verildiğinde:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Bir düzlemin vektör denkleminin formülü şöyledir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

Veya eşdeğer:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Altın

$\lambda$

$\mu$

Bunlar iki skalerdir, yani iki gerçek sayıdır.

Düzlemin parametrik denklemleri

Öte yandan düzlemin parametrik denkleminin formülü şöyledir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Düzlemin örtülü veya genel denklemi

Genel denklem olarak da adlandırılan bir planın örtülü denklemi, aşağıdaki determinantın çözülmesi ve sonucun 0’a ayarlanmasıyla elde edilir:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Böylece ortaya çıkan planın örtülü veya genel denklemi aşağıdaki biçimde olacaktır:

Bu tür düzlem denklemine Kartezyen düzlem denklemi de denir.

Düzlemin kanonik veya segmental denklemi

Bir düzlemin kanonik veya segmental denkleminin formülü aşağıdaki gibidir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Altın:

$a$

Bu, düzlem ile X ekseni arasındaki kesişme noktasıdır.
$b$

Bu, düzlem ile Y ekseni arasındaki kesişme noktasıdır.
$c$

Düzlemin Z ekseniyle kesiştiği yer burasıdır.

Bir düzleme normal vektör

Bir düzleme normal olan vektör, bu düzlemin içerdiği tüm doğrulara dik olan bir vektördür. Bu nedenle, bir düzleme normal olan bir vektör, onun düzleme dik olduğu anlamına gelir.

Uzaysal analitik geometrideki çoğu metrik problem, düzlemler ve onların normal vektörleriyle ilgilidir. Bu alıştırmaları çözmek için bir düzlem ile onun normal vektörü arasındaki matematiksel ilişkiyi bilmeniz yeterlidir:

Bir düzleme normal vektörün X, Y, Z bileşenleri , söz konusu düzlemin örtülü (veya genel) denkleminin sırasıyla A, B, C katsayılarıyla çakışır.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Altın

$\vv{n}$

vektör düzleme dik mi

$\pi.$

İki geometrik elemanın uzaydaki göreceli konumları

Açıkçası, bir çizginin veya düzlemin uzayda mutlaka yalnız olması gerekmez, aksine normal olarak birbirleriyle etkileşime girerler: kesişirler, paraleldirler, diktirler vb. Bu bölümde doğruların ve düzlemlerin farklı göreceli konumlarını ve bunların nasıl belirlendiğini göreceğiz.

Uzayda iki çizginin göreceli konumu

Analitik geometride, üç boyutlu bir uzayda (R3’te) çalışırken, iki çizgi arasında 4 olası göreceli konum vardır: iki çizgi çakışan çizgiler , paralel çizgiler , kesen çizgiler veya kesen çizgiler olabilir.

Paralel çizgiler

İki doğru aynı yöne sahip ancak ortak noktaları yoksa paraleldir. Ayrıca paralel çizgiler her zaman birbirlerinden aynı uzaklıkta olur.

Çakışan çizgiler

İki doğru, yönleri aynıysa ve tüm noktaları ortaksa çakışır.

Kavşak çizgileri

Kesişen iki doğrunun yönleri farklıdır ancak bir noktada birbirine değmektedir.

Kavşak çizgileri

Kesişen iki doğrunun yönleri farklıdır ve hiçbir noktada kesişmezler. Bu nedenle iki çapraz çizgi aynı düzlemde değildir. Örneğin çizginin üzerindeki grafiksel gösterimde

$s$

her zaman düz çizginin önündedir

$r$

Böylece birbirlerine asla dokunmayacaklar.

İki çizginin göreceli konumu aralıklara göre nasıl bulunur?

İki satırın göreceli konumunu bulmanın bir yolu, aşağıda göreceğimiz gibi, iki spesifik matrisin aralıklarını hesaplamaktır. Bu yöntem, iki doğru örtülü (veya genel) bir denklem biçiminde ifade edildiğinde çok kullanışlıdır.

Dolayısıyla, üç boyutlu uzayda (R3’te) örtülü (veya genel) denklemleriyle ifade edilen iki doğrumuz varsa:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

A, iki doğrunun katsayılarından oluşan matris olsun:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

Ve iki çizginin tüm parametrelerinden oluşan matris olan genişletilmiş A’ matrisi verildiğinde:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Daha sonra, iki çizginin göreceli konumu, aşağıdaki tabloya göre önceki iki matrisin boyutuna göre belirlenebilir:

iki satırın aralıklara göre göreceli konumları

Bu nedenle, iki sıra arasındaki bağıl konumu bulmak için her iki matrisin aralıklarını hesaplamamız gerekecek ve her matrisin aralığına bağlı olarak iki durumdan biri olacaktır.

Bu teorem, Rouché-Frobenius teoremi (doğrusal denklem sistemlerini çözmek için kullanılan bir yöntem) kullanılarak kanıtlanabilir, ancak bu sayfada ispatı yapmayacağız çünkü oldukça hantaldır ve fazla bir şey katmaz. .

İki düzlemin uzaydaki göreceli konumu

Analitik geometride iki düzlem arasında yalnızca üç olası göreceli konum vardır: kesişen düzlemler, paralel düzlemler ve çakışan düzlemler.

Kesişen Düzlemler : İki düzlem yalnızca bir doğru üzerinde kesişiyorsa kesişiyor demektir.
Paralel Düzlemler : İki düzlem herhangi bir noktada kesişmiyorsa paraleldir.
Çakışmalı Düzlemler : Tüm noktaları ortak olan iki düzlem çakışıktır.

Kesişen çekimler

paralel düzlemler

Eşleşen planlar

İki düzlemin göreceli konumu katsayılarla nasıl belirlenir

İki düzlem arasındaki göreceli konumu bilmenin bir yolu, bunların genel (veya örtülü) denklemlerinin katsayılarını kullanmaktır.

O halde iki farklı düzlemin genel (veya örtülü) denklemini düşünün:

$\pi_1 : \ Ax+By+Cz+D=0$

$\pi_2 : \ A'x+B'y+C'z+D'=0$

Üç boyutlu bir uzayda iki düzlem arasındaki göreceli konum, katsayılarının veya parametrelerinin orantılılığına bağlıdır:

parametrelerle iki düzlemin göreceli konumu

Böylece A, B veya C katsayılarından biri diğerleriyle orantılı olmadığında iki düzlem kesişecektir. Öte yandan, yalnızca bağımsız terimler orantılı olmadığında iki düzlem paralel olacaktır. Ve son olarak, iki denklemin tüm katsayıları orantılı olduğunda planlar çakışacaktır.

Uzaydaki mesafeler

Aşağıda farklı geometrik öğeler arasındaki mesafeyi hesaplamak için formüller bulunmaktadır: bir nokta ile bir çizgi arasında, iki düzlem arasında, bir düzlem ile bir çizgi arasında,…

İki nokta arasındaki mesafe

İki nokta arasındaki mesafe bu 2 noktanın belirlediği vektörün normuna karşılık gelir.

Yani iki genel noktamız varsa:

$A(a_x,a_y,a_z) \qquad \qquad B(b_x,b_y,b_z)$

İki nokta arasındaki mesafenin formülü:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(A,B) = \vert \vv{AB} \rvert = \sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2} \end{empheq}$

Bir noktadan bir çizgiye olan mesafe

Uzayda bir noktadan bir çizgiye olan mesafeyi hesaplamak için formül:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert} \end{empheq}$

Altın:

$\lvert \vv{\text{v}}_r \rvert$

çizginin yön vektörünün modülüdür

$r.$
$Q$

sağda bir nokta

$r,$

$P$

çizgi üzerinde bir nokta

$s$

Ve

$\vv{QP}$

iki nokta tarafından tanımlanan vektör
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

vektörler arasındaki vektör çarpımının modülüdür

$\vv{QP}$

Ve

$\vv{\text{v}}_r$

İki çizgi arasındaki mesafe

İki çizgi arasındaki mesafe göreceli konumlarına bağlıdır:

İki çizgi çakışırsa veya kesişirse , iki çizgi arasındaki mesafe sıfıra eşittir, çünkü bunlar (en azından) bir noktada kesişir.
İki doğru paralel veya kesiştiğinde duruma göre bir formül uygulanmalıdır (her iki açıklama da aşağıda mevcuttur).

İki paralel çizgi arasındaki mesafe

İki paralel çizgi birbirinden her zaman aynı uzaklıkta bulunur. Yani uzayda (R3’te) iki paralel çizgi arasındaki mesafeyi hesaplamak için bu, düzlemde (R2’de) olduğu gibi yapılır: sadece iki çizgiden birinin üzerinde bir nokta alıp oradaki mesafeyi bulmanız gerekir. bu noktadan diğer çizgiye kadardır.

uzayda iki paralel çizgi arasındaki mesafe

Bu nedenle, 2 paralel çizgi arasındaki mesafeyi belirlemek için bir nokta ile bir çizgi arasındaki mesafe formülünü kullanmanız gerekir.

Kesişen iki çizgi arasındaki mesafe

Yön vektörü ve kesişen iki çizginin herhangi bir noktası şöyle olsun:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

Kesişen iki çizgi arasındaki mesafenin formülü:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} \end{empheq}$

Altın:

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

vektörlerin karışık çarpımının mutlak değeridir

$\vv{\text{u}}, \vv{\text{v}}$

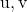
ve noktalarla tanımlanan vektör

$A$

Ve

$B$

.
$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

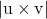
çapraz iki çizginin yön vektörleri arasındaki vektör çarpımının modülüdür.

Formül burada olmasına rağmen kesişen iki çizgi arasındaki mesafeyi belirlemek göründüğünden daha karmaşıktır. Yani eğer pratik yapmak isterseniz aşağıdaki linkte kesişen iki çizgi arasındaki mesafe ile ilgili örnekleri ve çözümlü alıştırmaları görebilirsiniz.

Bir noktadan bir düzleme olan mesafe

Bir nokta ve bir düzlemin genel (veya örtülü) denklemi verildiğinde:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

Bir noktadan düzleme olan mesafenin formülü:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}} \end{empheq}$

Formülü uygulayarak sıfıra eşit bir sonuç elde edersek, bu açıkça nokta ile düzlem arasındaki mesafenin sıfır olduğu ve dolayısıyla noktanın bu düzlemin parçası olduğu anlamına gelir.

İki düzlem arasındaki mesafe

Uzaydaki iki düzlem arasındaki mesafe, bu iki düzlem arasındaki göreceli konuma bağlıdır:

İki düzlem kesişiyor veya çakışıyorsa , belirli bir noktada kesiştikleri için aralarındaki mesafe sıfıra eşittir.
İki düzlem paralel ise, iki düzlem arasındaki mesafe, iki düzlemden birindeki bir nokta alınarak o noktanın diğer düzleme olan uzaklığı hesaplanarak hesaplanır.

İki paralel düzlem arasındaki mesafe

İki paralel düzlem birbirinden her zaman aynı uzaklıkta olduğundan, iki paralel düzlem arasındaki mesafeyi bulmak için iki düzlemden birinde bir nokta alabilir ve bu noktanın diğer düzleme olan mesafesini hesaplayabiliriz.

Yani iki paralel düzlem arasındaki mesafeyi hesaplamak için iki düzlemden birinde bir nokta bulmanız ve ardından bir nokta ile düzlem arasındaki mesafe formülünü kullanmanız gerekir.

Uzaydaki açılar

Mesafelerde olduğu gibi uzaydaki iki geometrik cisim arasındaki açının belirlenmesi de onların geometrik özelliklerine bağlıdır. Çünkü iki doğrunun oluşturduğu açıyı hesaplamak ile iki düzlemin oluşturduğu açıyı hesaplamak aynı şey değildir. Aşağıda çizgiler ve düzlemler arasındaki açıları bulmak için formüller var.

İki çizgi arasındaki açı

Öklid uzayında iki çizgi arasındaki açıyı bilmek için yön vektörlerinin oluşturduğu açıyı hesaplamamız gerekir, dolayısıyla:

İki farklı doğrunun yön vektörleri verildiğinde:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y,\text{u}_z)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

Bu iki doğrunun oluşturduğu açı aşağıdaki formülle hesaplanabilir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Altın

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

vektörlerin modülleri

$\vv{\text{u}}$

$\vv{\text{v}}$

sırasıyla.

Bir vektörün modülünün formülünün şöyle olduğunu hatırlayın:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

İki düzlem arasındaki açı

İki düzlem arasındaki açı, söz konusu düzlemlerin normal vektörlerinin oluşturduğu açıya eşittir. Bu nedenle iki düzlem arasındaki açıyı bulmak için normal vektörlerinin oluşturduğu açıyı hesaplarız çünkü bunlar eşdeğerdir .

İki farklı düzlemin genel (veya örtülü) denklemi göz önüne alındığında:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

Her düzlemin normal vektörü:

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

Ve bu iki düzlemin oluşturduğu açı, normal vektörlerinin oluşturduğu açı aşağıdaki formülle hesaplanarak belirlenir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

Bir doğru ile bir düzlem arasındaki açı

Bir doğru ile bir düzlemin oluşturduğu açı, doğrunun yön vektörü ile düzlemin normal vektörünün oluşturduğu birbirini tamamlayan iki açıdan küçük olanı olarak tanımlanır.

Bu nedenle eğer

$\vv{\text{v}}$

çizginin yön vektörüdür ve

$\vv{n}$

vektör düzleme normaldir:

$\vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

$\vv{n}=(n_x,n_y,n_z)$

Bir doğru ile bir düzlemin oluşturduğu açıyı hesaplamak için kullanılan formül:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \text{sen}(\alpha)=\cfrac{\lvert \vv{\text{v}} \cdot \vv{n}\rvert}{\lvert \vv{\text{v}} \rvert \cdot \lvert \vv{n} \rvert} \end{empheq}$

Uzayda analitik geometri (formüller)

Uzayda geometri nedir?

Uzaydaki çizginin denklemleri

Uzayda çizginin vektör denklemi

Uzaydaki çizginin parametrik denklemleri

Uzayda çizginin sürekli denklemi

Uzaydaki çizginin genel (veya örtülü) denklemleri

Uzayda düzlem denklemleri

Düzlemin vektör denklemi

Düzlemin parametrik denklemleri

Düzlemin örtülü veya genel denklemi

Düzlemin kanonik veya segmental denklemi

Bir düzleme normal vektör

İki geometrik elemanın uzaydaki göreceli konumları

Uzayda iki çizginin göreceli konumu

İki çizginin göreceli konumu aralıklara göre nasıl bulunur?

İki düzlemin uzaydaki göreceli konumu

İki düzlemin göreceli konumu katsayılarla nasıl belirlenir

Uzaydaki mesafeler

İki nokta arasındaki mesafe

Bir noktadan bir çizgiye olan mesafe

İki çizgi arasındaki mesafe

İki paralel çizgi arasındaki mesafe

Kesişen iki çizgi arasındaki mesafe

Bir noktadan bir düzleme olan mesafe

İki düzlem arasındaki mesafe

İki paralel düzlem arasındaki mesafe

Uzaydaki açılar

İki çizgi arasındaki açı

İki düzlem arasındaki açı

Bir doğru ile bir düzlem arasındaki açı

Yorum bırakın Yanıtı iptal et