Uzayda bir doğrunun bir düzleme uzaklığı

Burada bir çizgiden düzleme olan mesafenin nasıl hesaplandığını bulacaksınız ve ayrıca adım adım çözülmüş örnekleri ve alıştırmaları görebileceksiniz.

Bir çizgi ile bir düzlem arasındaki mesafe nedir?

Analitik geometride, uzayda bir çizgi ile bir düzlem arasındaki mesafe, bu iki geometrik eleman arasındaki göreceli konuma bağlıdır:

Doğru düzlemin içindeyse veya doğru ile düzlem paralelse onları ayıran mesafe sıfırdır.
Doğrunun düzleme paralel olması durumunda, doğrunun düzleme olan uzaklığı, doğru üzerinde herhangi bir nokta alınarak o noktadan düzleme olan uzaklık hesaplanarak bulunur.

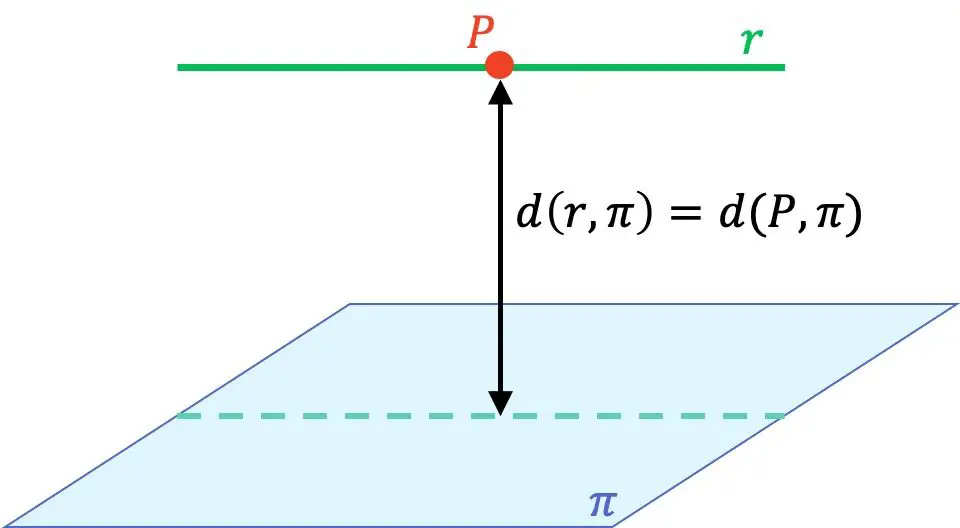
uzayda bir çizgiden bir düzleme olan mesafe

Bu nedenle, bir çizgiden düzleme olan mesafeyi hesaplamak için, bir çizgi ile düzlem arasındaki göreceli konumu nasıl belirleyeceğinizi ve bir nokta ile düzlem arasındaki mesafeyi nasıl hesaplayacağınızı bilmeniz önemlidir. Bu nedenle, tam olarak anlamadıysanız veya formülleri bilmiyorsanız, öncelikle bağlantılı sayfalara göz atmanızı öneririz; burada adım adım açıklamalar, örnekler ve çözülmüş alıştırmalar bulacaksınız.

Bir çizgi ile düzlem arasındaki mesafeyi hesaplama örneği

Uzayda (R3’te) bir doğru ile bir düzlem arasındaki mesafeyi nasıl bulacağınızı görebilmeniz için örnek olarak bir problemi çözeceğiz:

Çizgi ne kadar uzakta
$r$

uçakta

$\pi$

?

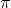
$\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}$

$\pi : \ 4x+2y+z-6=0$

Doğru ile düzlem arasındaki mesafeyi bulmak için öncelikle ikisi arasındaki göreceli konumu bilmeniz gerekir.

Bir yandan çizgi parametrik denklemler biçiminde tanımlanır, dolayısıyla yön vektörü ve içinden geçtiği nokta şöyledir:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}$

Ve diğer taraftan düzleme normal olan vektör:

$\vv{n} =(4,2,1)$

Bu nedenle, düzlem ile çizgi arasındaki göreceli konumu belirlemek için, çizginin yön vektörü ile düzleme dik vektör arasındaki skaler çarpımı hesaplamak gerekir:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}$

Nokta çarpımın sonucu sıfırdır, dolayısıyla çizgi yalnızca düzlemin içinde yer alabilir veya ona paralel olabilir. Hangi durumun olduğunu bulmak için doğru üzerindeki noktanın Kartezyen koordinatlarını düzlem denkleminde yerine koyarız:

$4x+2y+z-6=0 \ \xrightarrow{P(-2,1,-1)} \ 4\cdot (-2) +2\cdot 1 -1-6= 0$

$-8+2-1-6 = 0$

$-13 \neq 0$

Doğrunun noktasını düzlem denkleminde değiştirerek bir eşitsizlik elde ederiz, bu nedenle nokta düzlemin denklemine uymaz ve sonuç olarak doğru ve düzlem paraleldir.

Doğrunun ve düzlemin paralel olduğunu bildiğimizde artık aralarındaki geometrik mesafeyi hesaplayabiliriz. Bunu yapmak için doğru üzerindeki noktayı alıp o noktadan düzleme olan mesafeyi hesaplıyoruz.

$P(-2,1,-1) \qquad \qquad \pi: \ 4x+2y+z-6=0$

Bu nedenle, bir noktadan düzleme olan mesafe için formülü kullanırız:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Şimdi her bilinmeyenin değerini formülde yerine koyuyoruz:

$d(P,\pi) = \cfrac{\lvert 4\cdot (-2)+2\cdot 1+1\cdot (-1)-6\rvert}{\sqrt{4^2+2^2+1^2}}$

Ve son olarak işlemleri gerçekleştiriyoruz:

$d(P,\pi) = \cfrac{\lvert -8+2-1-6\rvert}{\sqrt{16+4+1}}$

$d(P,\pi) = \cfrac{\lvert -13\rvert}{\sqrt{21}}$

$d(P,\pi) = \cfrac{13}{\sqrt{21}}$

Böylece doğru ile düzlem arasındaki mesafe, nokta ile hesaplanan düzlem arasındaki mesafeye eşit olur:

$\bm{d(r,\pi)=d(P,\pi) = }\cfrac{\bm{13}}{\bm{\sqrt{21}}}$

Açıkçası mesafe bize her zaman pozitif bir değer vermelidir çünkü mesafeler her zaman pozitiftir. Olumsuz sonuç alıyorsak adım atarken hata yapmışız demektir.

Uzayda bir çizgiden bir düzleme olan mesafe

Bir çizgi ile bir düzlem arasındaki mesafe nedir?

Bir çizgi ile düzlem arasındaki mesafeyi hesaplama örneği

Yorum bırakın Yanıtı iptal et