Üst ve alt üçgen matris

Bu sayfada üçgen matrisin ne olduğunu ve farklı üçgen matris türlerini örneklerle birlikte göreceksiniz. Ayrıca bir üçgen matrisin determinantının nasıl hesaplanacağını ve bu çok ilginç matrisin özelliklerinin neler olduğunu öğreneceksiniz. Son olarak Hessenberg matrisinin ne olduğunu da açıklıyoruz çünkü üçgensel matrislerle ilişkili bir matristir.

Üçgen matris nedir?

Üçgen matrisin tanımı:

Üçgen matris, ana köşegenin üstündeki veya altındaki tüm elemanların sıfır (0) olduğu bir kare matristir.

Üçgen matrisler doğrusal cebir hesaplamalarında yaygın olarak kullanılır, çünkü bir üçgen matrisi ters çevirmek, determinantını hesaplamak ve hatta doğrusal denklem sistemlerini bu tür matrislerle çözmek, tüm konumlarda 0’dan farklı öğelere sahip matrislerden çok daha kolaydır. .

üst üçgen matris

Üst üçgen matris, ana köşegenin altındaki elemanları sıfır (0) olan bir kare matristir.

Üst üçgen matris örneği:

alt üçgen matris

Alt üçgen matris, ana köşegenin üzerindeki her öğesinde sıfır (0) bulunan bir kare matristir.

Alt üçgen matris örneği:

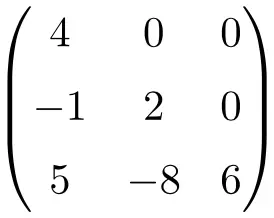
Bazen bu matrisler üst üçgen matris için U harfiyle, alt üçgen matris için L harfiyle de adlandırılır. Bu terminoloji çoğunlukla İngilizce olarak kullanılmasına rağmen, aslında U üst üçgen matrisi , L ise alt üçgen matrisi temsil eder.

Üçgen matris örnekleri

2 × 2 boyutlu üçgen matris

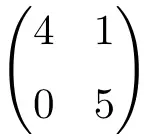
3×3 mertebesinden üçgen matris

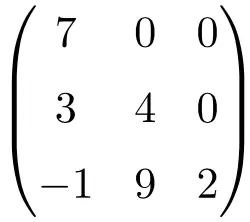
4×4 boyutunda üçgen matris

Üçgensel bir matrisin determinantı

Bir üçgen matrisin determinantı , ister üst ister alt üçgen olsun, ana köşegen üzerindeki elemanların çarpımıdır.

Determinantını bulmak için üçgen matrisin ana köşegeninin elemanlarının çarpımını hesaplamanın nasıl yeterli olduğunu çözen aşağıdaki alıştırmaya bir göz atın:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Bu teorem kolayca kanıtlanabilir: bir üçgen matrisin determinantını bloklara (veya kofaktörlere) göre hesaplayın. Bu gösterim aşağıda genel bir üçgen matris kullanılarak detaylandırılmıştır:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Öte yandan, bir matrisin determinantı 0’dan farklıysa tersinir olduğunu biliyoruz. Yani, ana köşegendeki hiçbir öğe 0 değilse, üçgen matris de tersinir olacak ve dolayısıyla düzenli olacaktır. matris.

Üçgen matrisin özellikleri

Şimdi üçgen matrislerin özelliklerinin neler olduğunu görelim:

İki üst üçgen matrisin çarpımı bir üst üçgen matrise eşittir. Ve bunun tersi de geçerlidir: iki alt üçgen matrisin çarpılması başka bir alt üçgen matris verir.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

Bir üst üçgen matrisin transpozu bir alt üçgen matristir ve bunun tersi de geçerlidir: bir alt üçgen matrisin transpozu bir üst üçgen matristir.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Üçgen bir matris, ana köşegendeki tüm elemanları sıfır değilse, yani sıfırdan farklıysa tersinirdir . Böyle bir durumda bir üst (alt) üçgen matrisin tersi aynı zamanda bir üst (alt) üçgen matristir.

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Ek olarak, ters çevrilmiş matrisin ana köşegeni her zaman orijinal üçgen matrisin ana köşegeninin elemanlarının terslerini içerecektir.

Herhangi bir diyagonal matris hem bir üst üçgen matris hem de bir alt üçgen matristir, örneğin:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Yani bir skaler matris aynı zamanda bir üst ve alt üçgen matristir. Örneğin kimlik matrisi:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Açıkçası, sıfır matrisi aynı zamanda bir üst ve alt üçgen matristir, çünkü ana köşegenin üstündeki ve altındaki elemanlar 0’dır:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Üçgen bir matrisin özdeğerleri (veya özdeğerleri), ana köşegenin elemanlarıdır.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Bir üst veya alt üçgen matris her zaman özvektörler (veya özvektörler) temelinde köşegenleşme yeteneğine sahiptir .

Herhangi bir matris, bir alt üçgen matris ile bir üst üçgen matrisin çarpımına ayrılabilir . Yani herhangi bir matris üçgen matris çarpımına dönüştürülebilir. Ayrıca matris tersinir ise bu dönüşüm benzersizdir. Bir matrisi çarpanlara ayırmak için sıklıkla LU ayrıştırma yöntemi kullanılır.

Bir matrisi üçgenleştirme

Tabanı değiştirerek üçgenleştirilebilen matrislerle ilgili çeşitli teoremler vardır. Ancak burada Gauss yönteminde olduğu gibi çizgilere temel dönüşümler uygulayarak bir matrisin nasıl üçgenleştirileceğini göreceğiz.

Örneğin:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

Ve bu şekilde orijinal matrisi zaten üçgenleştirdik.

Gauss yönteminde çizgiler arasında yetkilendirilen temel dönüşümlerin şöyle olduğunu hatırlayın:

Bir çizgiyi diğer çizgilerin doğrusal birleşimiyle değiştirin.
Bir satırdaki tüm terimleri 0’dan farklı bir sayıyla çarpın veya bölün.
Sipariş satırlarını düzenleyin.

Hessenberg matrisi

Hessenberg matrisinin tanımı şu şekildedir:

Hessenberg matrisi “neredeyse” üçgen bir matristir, yani ilk alt köşegenden (üst Hessenberg matrisi) veya ilk süper köşegenden (alt Hessenberg matrisi) başlayarak tüm elemanları sıfırdır.

Bunun en iyi şekilde bir üst Hessenberg matrisi örneği ve başka bir alt Hessenberg matrisi örneğiyle anlaşıldığına eminim:

Üst Hessenberg matrisi

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Alt Hessenberg matrisi

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Hem üst hem de alt Hessenberg matrisi olan bir matris, üç köşegen bir matristir .

Bu matris, adını 20. yüzyılın önde gelen Alman mühendis ve matematikçisi Karl Hessenberg’den almıştır.

Son olarak, bu tür bir matrisin özelliği, bir üçgen matrisle çarpılması durumunda sonucun her zaman bir Hessenberg matrisi olmasıdır.