Üç vektörün karışık çarpımı (veya üçlü nokta çarpımı)

Bu sayfada üç vektörün (veya üçlü nokta çarpımının) karma çarpımının ne olduğunu ve nasıl hesaplandığını açıklıyoruz. Ayrıca vektörler arasında bu tür işlemlere ilişkin örnekler, alıştırmalar ve çözülmüş problemler göreceksiniz. Ayrıca karışık ürünün özelliklerini ve uygulamalarını da bulacaksınız.

Üç vektörün karışık çarpımı nedir?

Üç vektörün karışık çarpımı , aynı zamanda üçlü nokta çarpımı olarak da adlandırılır, iki farklı işlem türünü içeren üç vektörün ardışık çarpımıdır: nokta çarpım ve vektör çarpımı . Yani, iki vektör işleminin birleşimi bir skaler (gerçek sayı) verir.

Somut olarak, karma çarpım, iki vektörün vektör çarpımının hesaplanmasından ve ardından elde edilen sonucun üçüncü bir vektörle vektörel olarak çarpılmasından oluşur. Bu şekilde yazınca çok karmaşık görünebilir ama gerçekte o kadar da değil, üçlü nokta çarpım formülüne bakın:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})$

Formülünde görebileceğiniz gibi üç vektörün karışık çarpımı iki köşeli parantezle gösterilmiştir.

Üç vektörün karma çarpımı nasıl hesaplanır?

Üçlü nokta çarpım formülü önceki bölümde gördüğümüz formüldür, ancak genellikle üç vektörün karma çarpımını belirlemek için kullanılmaz çünkü daha basit ve daha hızlı başka bir yol vardır:

Herhangi 3 vektör şöyle olsun:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)\qquad \vv{\text{w}}= (\text{w}_x,\text{w}_y,\text{w}_z)$

Üç vektör arasındaki karışık çarpımı hesaplamak için, vektörlerin bileşenlerinin oluşturduğu 3×3 determinantı çözmeniz yeterlidir:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}$

Bunun nasıl hesaplandığına dair bir örnek görebilirsiniz. Aşağıdaki üç vektörün karma çarpımını bulacağız:

$\vv{\text{u}}= (1,2,0) \qquad \vv{\text{v}}= (0,-1,3)\qquad \vv{\text{w}}= (-2,4,1)$

Karışık çarpımı belirlemek için, vektörleri matrisin satırlarına yerleştirerek 3. dereceden bir determinant oluştururuz:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

Ve şimdi sadece matrisin determinantını çözmemiz gerekiyor, bunun için herhangi bir yöntemi kullanabilirsiniz. Bu durumda Sarrus kuralını uygulayacağız (ancak bu toplamalar veya eşçarpanlarla da yapılabilir):

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}$

İki prosedürün eşdeğer olduğunu göstermek için aynı vektörlerin karma çarpımını tanımlarından yararlanarak hesaplayacağız:

$\begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}$

Daha hızlı olduğundan ve hata yapma şansı daha az olduğundan, karışık çarpımı vektörlerin determinantı üzerinden hesaplamanızı öneririz. Ancak gördüğünüz gibi hangi yöntemi kullanırsanız kullanın sonuç aynı olduğundan hangisini tercih ederseniz onu kullanın. 👍

Karışık ürünün geometrik yorumu

Üç vektörün karma çarpımını nasıl bulacağınızı öğrendikten sonra merak ediyor olabilirsiniz… karma çarpım ne işe yarar? Matematikte bunun iki ana kullanımı vardır: paralelyüzlü bir nesnenin hacmini ve bir tetrahedronun hacmini hesaplamak.

Paralel borunun hacmi, geometrik alanın 3 boyutunu gösteren vektörlerin karışık çarpımının mutlak değerine eşittir.

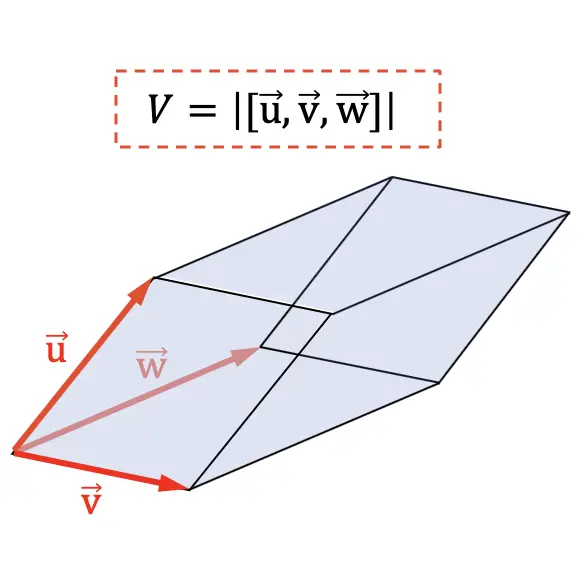
üç vektörün karışık çarpımına veya üçlü skaler çarpıma örnek

Karışık ürünün bir başka uygulaması da bir tetrahedronun hacminin belirlenmesidir. Karışık çarpımın mutlak değerinin geometrik olarak altıncı kısmı bir tetrahedronun hacmini temsil ettiğinden:

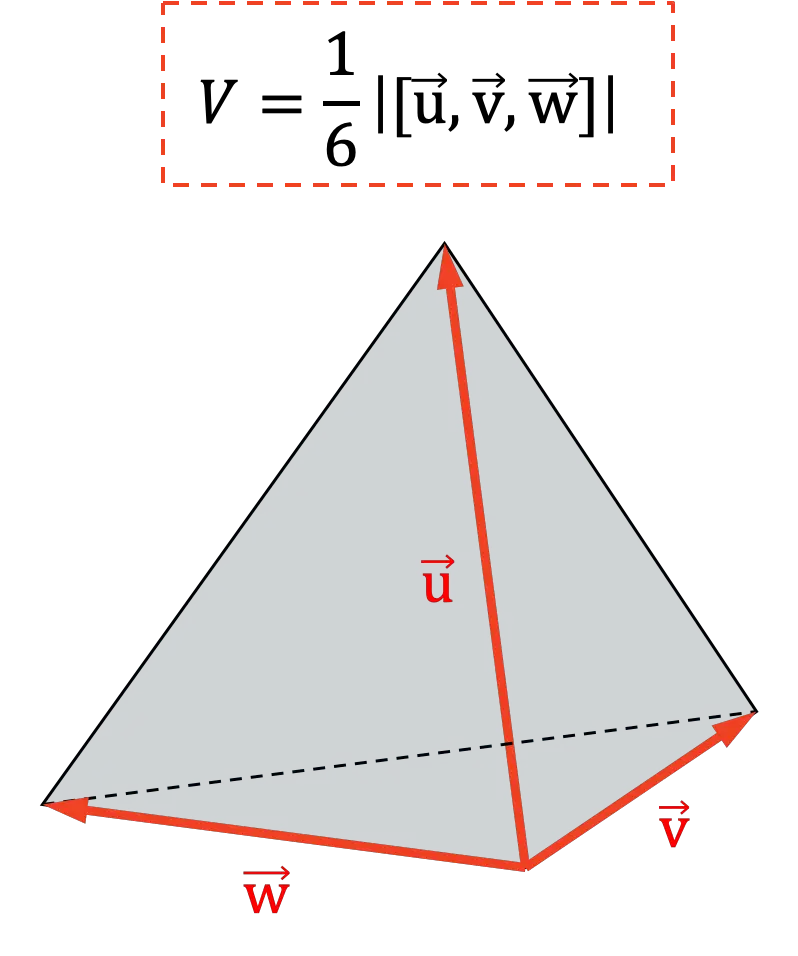
Karışık ürünün veya üçlü nokta ürününün özellikleri

Karışık çarpım veya üçlü skaler çarpım aşağıdaki özelliklere sahiptir:

Genel olarak, karışık çarpım vektörlerinin sırasındaki bir değişiklik aynı zamanda işarette de bir değişiklik anlamına gelir. Bu nedenle karma çarpım vektörlerinin sırası önemlidir.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{v}},\vv{\text{u}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{u}},\vv{\text{w}},\vv{\text{v}}\bigr] = - \bigl[\vv{\text{w}},\vv{\text{v}},\vv{\text{u}}\bigr]$

Ancak sırayı döngüsel olarak değiştirirsek işaret değişmez:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \bigl[\vv{\text{v}},\vv{\text{w}},\vv{\text{u}}\bigr] = \bigl[\vv{\text{w}},\vv{\text{u}},\vv{\text{v}}\bigr]$

Üç boyutlu bir uzayda (R3’te), doğrusal olarak bağımlı veya eş düzlemli üç vektörün (aynı düzleme ait) karışık çarpımı 0’a eşittir.

Karışık ürün sorunları düzeltildi

1. Egzersiz

Verilen 3 vektör:

$\vv{\text{u}}= (3,-1,2) \qquad \vv{\text{v}}= (-2,0,1)\qquad \vv{\text{w}}= (5,1,-1)$

Üç vektörün karışık çarpımını hesaplayın:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

Çözüme bakın

Karışık çarpımını bulmak için vektörlerin koordinatlarından oluşan determinantı çözmeliyiz:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}$

Alıştırma 2

Verilen 3 vektör:

$\vv{\text{u}}= (7,2,-3) \qquad \vv{\text{v}}= (2,4,9)\qquad \vv{\text{w}}= (4,3,-1)$

Üç vektör arasındaki karışık çarpımı belirleyin:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

Çözüme bakın

Karma çarpımını bulmak için, vektörlerin Kartezyen koordinatlarına doğru şeklinde sahip olan determinantı çözmemiz gerekir:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}$

Alıştırma 3

3 kenarı aşağıdaki vektörlere eşit olan paralelyüzün hacmini hesaplayınız:

$\vv{\text{u}}= (0,2,5) \qquad \vv{\text{v}}= (-1,6,2)\qquad \vv{\text{w}}= (3,1,2)$

Çözüme bakın

Bir paralelyüzün hacmi, kenar olarak sahip olduğu vektörlerden 3’ünün karışık çarpımının mutlak değerine eşittir. Bu nedenle öncelikle vektörlerin üçlü çapraz çarpımını hesaplıyoruz:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}$

Böylece paralelyüzün hacmi, karışık çarpımın sonucunun mutlak değeri olur:

$V= \lvert -79 \rvert = \bm{79}\ \mathbf{u}\bm{^3}$

Alıştırma 4

Köşeleri aşağıdaki noktalar olan tetrahedronun hacmini hesaplayın:

$A(1,0,2) \qquad B(3,3,2)\qquad C(5,-1,4)\qquad D(4,2,1)$

Çözüme bakın

İlk olarak tetrahedronun kenarlarını temsil eden vektörleri hesaplıyoruz:

$\vv{AB}=B-A= (3,3,2)-(1,0,2)=(2,3,0)$

$\vv{AC}=C-A= (5,-1,4)-(1,0,2)=(4,-1,2)$

$\vv{AD}=D-A= (4,2,1)-(1,0,2)=(3,2,-1)$

Bir tetrahedronun hacmi, kenarları için sahip olduğu 3 vektörün karışık çarpımının mutlak değerinin altıda birine eşittir. Bu nedenle öncelikle bulunan vektörlerin karma çarpımını hesaplıyoruz:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}$

Böylece tetrahedronun hacmi, karışık ürünün mutlak değerinin altıda biri olacaktır:

$V= \cfrac{1}{6} \cdot \lvert 24 \rvert = \cfrac{24}{6} = \bm{4} \ \mathbf{u}\bm{^3}$

Üç vektörün karışık çarpımı nedir?

Üç vektörün karma çarpımı nasıl hesaplanır?

Karışık ürünün geometrik yorumu

Karışık ürünün veya üçlü nokta ürününün özellikleri

Karışık ürün sorunları düzeltildi

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et