Trigonometrik sınırlar -

Burada trigonometrik limitlerin nasıl çözüleceğini öğreneceksiniz. Trigonometrik fonksiyonların limitleriyle ilgili birkaç örnek görebileceksiniz ve hatta trigonometrik limitlerle ilgili adım adım çözümlü alıştırmalar yapabileceksiniz.

Trigonometrik limitler nelerdir?

Trigonometrik limitler trigonometrik fonksiyonlar üzerinde hesaplanan limitlerdir. Trigonometrik limitleri çözmek için bir ön prosedür uygulanmalıdır çünkü bunlar genellikle belirsizliklere yol açar.

Ayrıca trigonometrik fonksiyonlar periyodik fonksiyonlar olduğundan sonsuz limitleri yoktur. Yani grafikleri belirli bir değere yönelmeden periyodik olarak sürekli tekrarlanır.

Trigonometrik Limit Formülleri

Tüm trigonometrik sınırlar aşağıdaki iki formülden hesaplanır:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

Formül gösterimi

Limiti ikame yoluyla hesaplamaya çalışırsak sıfır arasında sıfır belirsizliğini elde ederiz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=\frac{\text{sen}(0)}{0}=\frac{0}{0}$

Ancak bu trigonometrik formül, daha yakın fonksiyonun ve x=0’a (radyan cinsinden açılar) daha yakın değerlerin hesaplanmasıyla gösterilebilir.

$\displaystyle f(x)=\frac{\text{sen}(x)}{x}=1$

$\begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}$

$\begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}$

Trigonometrik fonksiyonun iki yanal limiti 1 verir, dolayısıyla x=0 noktasındaki limit 1’dir:

$\begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}$

Böylece, x 0’a yaklaşırken sinüs x’in x’e bölümünün trigonometrik limiti 1’e eşittir.

Bu formül aynı zamanda birkaç açı için de uygulanabilir:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(kx)}{kx}=1$

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

Formül gösterimi

Limiti doğrudan yerine koyma yoluyla bulmaya çalışırsak, sıfır arasında belirsiz sıfır formunu elde ederiz:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=}\frac{1-\text{cos}(0)}{0}=\frac{1-1}{0}=\frac{0}{0}$

Ancak eşitliği yukarıdaki formülden kontrol edebiliriz. Bunu yapmak için önce kesrin payını ve paydasını 1 artı x’in kosinüsüyle çarpmanız gerekir:

$\displaystyle\lim_{x\to 0}\frac{\bigl(1-\text{cos}(x)\bigr)\cdot \bigl(1+\text{cos}(x)\bigr)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

Artık kesrin payının dikkate değer özdeşliğine sahibiz, dolayısıyla onu basitleştirebiliriz:

$\displaystyle\lim_{x\to 0}\frac{1^2-\text{cos}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

Temel trigonometrik özdeşlikten başlayarak payı yeniden yazıyoruz:

$\text{sen}^2(x)+\text{cos}^2(x)=1 \ \longrightarrow \ \text{sen}^2(x)=1-\text{cos}^2(x)$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

Bu nedenle kesirleri kesirlerin çarpımına dönüştürebiliriz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)\cdot \text{sen}(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{\text{sen}(x)}{1+\text{cos}(x)}$

Limitlerin özelliklerini kullanarak yukarıdaki ifadeyi limitlerin çarpımına dönüştürebiliriz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

Yukarıda gösterilen formülü kullanarak trigonometrik limiti kolayca basitleştirebiliriz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

$\displaystyle 1\cdot \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

$\displaystyle \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

Ve son olarak ortaya çıkan limiti hesaplıyoruz:

$\displaystyle \lim_{x\to 0}\frac{\text{sen}(0)}{1+\text{cos}(0)}=\frac{0}{1+1}=\frac{0}{2}=0$

Bu nedenle trigonometrik limit formülü doğrulanır:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

Diğer formülde olduğu gibi birden fazla açı için de kullanılabilir:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(kx)}{kx}=0$

Bu nedenle trigonometrik limitleri çözmek için aritmetik kullanarak fonksiyonları dönüştürmeliyiz ve bunlara benzer ifadeler elde etmeliyiz. Bu şekilde iki formülden birini kullanabilir ve limitin değerini bulabiliriz.

Öte yandan bazen belirli trigonometrik özdeşlikleri uygulamamız gerekebilir, bu nedenle aşağıdaki formüllerin tamamını size bırakıyoruz.

Trigonometrik kimlikler

Üç ana trigonometrik oranı birbirine bağlayan formül:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Temel trigonometrik kimlik:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

Temelden türetilen trigonometrik ilişkiler:

$1+\text{tan}^2 (x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)$

$1+\text{cot}^2 (x)=\cfrac{1}{\text{sen}2(x)}=\text{cosec}^2(x)$

Zıt açılar:

$\text{sen}(-x)=-\text{sen}(x)$

$\text{cos}(-x)=\text{cos}(x)$

$\text{tan}(-x)=-\text{tan}(x)$

İki açının toplamı:

$\text{sen}(x+y)=\text{sen}(x)\text{cos}(y)+\text{cos}(x)\text{sen}(y)$

$\text{cos}(x+y)=\text{cos}(x)\text{cos}(y)-\text{sen}(x)\text{sen}(y)$

$\text{tan}(x+y)=\cfrac{\text{tan}(x)+\text{tan}(y)}{1-\text{tan}(x)\text{tan}(y)}$

İki açının farkı:

$\text{sen}(x-y) = \text{sen}(x)\text{cos}(y)-\text{cos}(x)\text{sen}(y)$

$\text{cos}(x-y) = \text{cos}(x)\text{cos}(y)+ \text{sen}(x) sen(y)$

$\text{tan}(x-y)=\cfrac{\text{tan}(x)-\text{tan}(y)}{1+\text{tan}(x)\text{tan}(y)}$

Çift açı:

$\text{sen}(2x) = 2\text{sen}(x)\text{cos}(x)$

$\text{cos}(2x) =\text{cos}^2(x)-\text{sen}^2(x)$

$\text{tan}(2x) =\cfrac{2\text{tan}(x)}{1-\text{tan}^2(x)}$

Yarım açı:

$\displaystyle \text{sen}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1-\text{cos}(x)}{2}}$

$\displaystyle \text{cos}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1+\text{cos}(x)}{2}}$

$\displaystyle\text{tan}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1-\text{cos}(x)}{1+\text{cos}(x)}}$

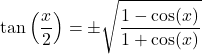
Sinüs ve kosinüsün eklenmesi ve çıkarılması:

$\displaystyle \text{sen}(x)+\text{sen}(y)=2\text{sen}\left(\frac{x+y}{2} \right)\text{cos}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{sen}(x)-\text{sen}(y)=2\text{cos}\left(\frac{x+y}{2} \right)\text{sen}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{cos}(x)+\text{cos}(y)=2\text{cos}\left(\frac{x+y}{2} \right)\text{cos}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{cos}(x)-\text{cos}(y)=-2\text{sen}\left(\frac{x+y}{2} \right)\text{sen}\left(\frac{x-y}{2} \right)$

Sinüs ve kosinüslerin çarpımı:

$\displaystyle \text{sen}(x)\cdot \text{sen}(y)=\frac{1}{2}\Bigl[\text{cos}(x-y)-\text{cos}(x+y)\Bigr]$

$\displaystyle \text{cos}(x)\cdot \text{cos}(y)=\frac{1}{2}\Bigl[\text{cos}(x+y)+\text{cos}(x-y)\Bigr]$

$\displaystyle \text{sen}(x)\cdot \text{cos}(y)=\frac{1}{2}\Bigl[\text{sen}(x+y)+\text{sen}(x-y)\Bigr]$

Trigonometrik limitlerin tam olarak nasıl hesaplandığını görebilmeniz için aşağıda adım adım bir örnek hazırladık.

Trigonometrik limit örneği

Aşağıdaki örneği kullanarak trigonometrik bir limitin nasıl çözüldüğünü görelim:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}$

Trigonometrik limiti hesaplamaya çalışırken sıfırın sıfır arasındaki belirsizliğini elde ederiz:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}=\frac{\text{tan}(0)}{0}=\frac{0}{0}$

➤ Bakınız: sıfır arasında sıfır limit

Bu nedenle limiti çözmek için trigonometrik fonksiyonu dönüştürmek gerekir. Teğet fonksiyonu sinüs bölü kosinüse eşittir, yani:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}=\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{x}$

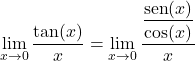
Artık kesirlerin özelliklerini uygulayarak fonksiyonu bir çarpım olarak ifade edebiliriz:

$\displaystyle\frac{\displaystyle\frac{a}{b}}{\displaystyle\frac{c}{d}}=\frac{a\cdot d}{b\cdot c}$

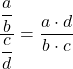
$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}$

Limitlerin özelliklerini kullanarak, çarpılan iki fonksiyonun limitini iki limitin çarpımına dönüştürebiliriz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\frac{1}{\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}$

Yukarıda gösterdiğimiz gibi ilk trigonometrik limit 1 verir:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}=1\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}=\lim_{x\to 0}\frac{1}{\text{cos}(x)}$

O halde aşağıdaki hesaplamayı yapın:

$\displaystyle \lim_{x\to 0}\frac{1}{\text{cos}(x)}=\frac{1}{\text{cos}(0)}=\frac{1}{1}=1$

Trigonometrik limitlerle ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki trigonometrik limiti çözün:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}$

Çözümü görün

Öncelikle doğrudan değerlendirme yoluyla trigonometrik limiti hesaplamaya çalışıyoruz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}=\frac{\text{sen}(4\cdot 0)}{2\cdot 0}=\frac{0}{0}$

Ancak sıfır üzeri sıfır belirsizliği elde ederiz. Bu yüzden fonksiyona dönüşümler uygulamamız gerekiyor.

Öncelikle aşağıdakileri yaparak x’i paydada bırakacağız:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}=\lim_{x\to 0}\frac{1}{2}\cdot\frac{\text{sen}(4x)}{x}=\frac{1}{2}\cdot\lim_{x\to 0}\frac{\text{sen}(4x)}{x}$

Şimdi trigonometrik sınırlar için ilk formülün uygulanabileceği bir ifade elde etmek için kesri 4’e bölüyoruz:

$\displaystyle\frac{1}{2}\lim_{x\to 0}\frac{\text{sen}(4x)\cdot 4}{x\cdot 4}=\frac{1}{2}\cdot 4 \cdot \lim_{x\to 0}\frac{\text{sen}(4x)}{4x}=2\lim_{x\to 0}\frac{\text{sen}(4x)}{4x}$

Son olarak başta gördüğümüz formülü uyguluyoruz ve trigonometrik limiti çözüyoruz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(kx)}{kx}=1$

$\displaystyle 2\lim_{x\to 0}\frac{\text{sen}(4x)}{4x}=2\cdot 1=\bm{2}$

Alıştırma 2

Aşağıdaki trigonometrik limiti hesaplayın:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}$

Çözümü görün

İlk önce trigonometrik limiti bulmaya çalışıyoruz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}=\frac{\text{sen}(0)+\text{tan}(0)}{0}=\frac{0}{0}$

Ancak sıfıra karşılık gelen belirsiz formda sıfıra ulaşılır.

Daha sonra tanjantı sinüs ve kosinüsün bir bölümüne dönüştürürüz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}=\lim_{x\to 0}\frac{\displaystyle\text{sen}(x)+\frac{\text{sen}(x)}{\text{cos}(x)}}{x}$

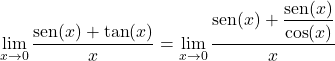
x’in kosinüsüyle çarpıp bölüyoruz:

$\displaystyle\lim_{x\to 0}\frac{\left(\displaystyle\text{sen}(x)+\frac{\text{sen}(x)}{\text{cos}(x)}\right)\cdot\text{cos}(x)}{x\cdot\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)\text{cos}(x)+\text{sen}(x)}{x\cdot\text{cos}(x)}$

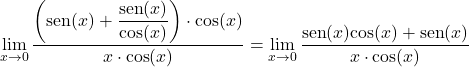
Payda ortak bir faktör alıyoruz ve trigonometrik limiti ikiye ayırıyoruz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)(\text{cos}(x)+1)}{x\cdot\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{\text{cos}(x)+1}{\text{cos}(x)}$

Ve son olarak trigonometrik limitin sonucunu buluyoruz:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{\text{cos}(x)+1}{\text{cos}(x)}=1\cdot\frac{\text{cos}(0)+1}{\text{cos}(0)} =\frac{1+1}{1}=\bm{2}$

Alıştırma 3

Aşağıdaki trigonometrik fonksiyonun limitini x sıfıra yaklaşırken çözün:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)-\text{sen}{(x)}}{3x\cdot\text{tan}(x)}$

Çözümü görün

Doğrudan hesaplamayı yaparak 0 arasındaki belirsiz sınır olan 0’ı elde ederiz:

$\displaystyle\lim_{x\to 0}}\frac{\text{tan}(x)-\text{sen}(x)}{3x\cdot\text{tan}(x)}=\frac{\text{tan}(0)-\text{sen}(0)}{3\cdot 0\cdot\text{tan}(0)}=\frac{0}{0}$

Böylece her terimi x’in tanjantına bölerek limiti basitleştireceğiz:

$\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{tan}(x)}{\text{tan}(x)}-\frac{\text{sen}(x)}{\text{tan}(x)}}{\displaystyle\frac{3x\cdot\text{tan}(x)}{\text{tan}(x)}}=\lim_{x\to 0}\frac{\displaystyle 1-\frac{\text{sen}(x)}{\text{tan}(x)}}{3x}$

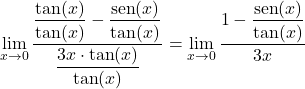
İkinci olarak, temel trigonometrik özdeşlikten payın kesirinin x’in kosinüsüne eşdeğer olduğu sonucunu çıkarabiliriz:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}\ \longrightarrow \ \text{cos}(x)=\cfrac{\text{sen}(x)}{\text{tan}(x)}$

$\displaystyle\lim_{x\to 0}\frac{\displaystyle 1-\frac{\text{sen}(x)}{\text{tan}(x)}}{3x}=\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}$

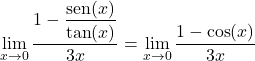
Trigonometrik limitler teorisinde gösterilen ikinci formülü uygulayarak limiti kolaylıkla çözebiliriz:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}$

Alıştırma 4

x=0 noktasında aşağıdaki trigonometrik limitin çözümünü belirleyin:

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}$

Çözümü görün

Limiti çözmeye çalışırsak 0/0 belirsiz formunu buluruz:

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}=\frac{2\text{sen}(0)\text{cos}(0)\text{sen}(5\cdot 0)}{0^2}=\frac{0}{0}$

Payın cebirsel ifadesi, çift açının sinüsünün trigonometrik özdeşliği kullanılarak yeniden yazılabilir:

$\text{sen}(2x)=2\text{sen}(x)\text{cos}(x)$

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}=\lim_{x\to 0}\frac{\text{sen}(2x)\text{sen}(5x)}{x^2}$

Şimdi trigonometrik fonksiyonun limitini bir çarpıma ayıralım:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}$

Ve son olarak limitlerin özelliklerini uygulayarak trigonometrik limiti çözüyoruz:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}$

Trigonometrik limitler nelerdir?

Trigonometrik Limit Formülleri

Trigonometrik limit örneği

Trigonometrik limitlerle ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et