Bu sayfada bunun ne olduğunu ve bir matrisin tersinin determinantlar yöntemi (veya ek matris) ve Gauss yöntemiyle nasıl hesaplanacağını öğreneceksiniz. Ayrıca ters matrisin tüm özelliklerini göreceksiniz ve ayrıca her yöntem için adım adım çözülmüş örnekler ve alıştırmalar bulacaksınız, böylece bunları tamamen anlayabilirsiniz. Son olarak, 2×2’lik bir matrisi hızlı bir şekilde tersine çevirmek için bir formülü ve hatta bu matris işleminin en büyük faydasını açıklıyoruz: bir doğrusal denklem sistemini çözme.
Bir matrisin tersi nedir?
Olmak
![]()
bir kare matris. Ters matrisi
![]()
yazılmış
![]()
ve aşağıdakileri sağlayan da bu matristir:
![]()
![]()
Altın
![]()
Kimlik matrisidir.
Bir matrisi ne zaman tersine çevirebilirsin ve ne zaman yapamazsın?
Bir matrisin tersinirliğini belirlemenin en basit yolu onun determinantını kullanmaktır:
- Söz konusu matrisin determinantının 0’dan farklı olması matrisin tersinir olduğu anlamına gelir. Bu durumda bunun düzenli bir matris olduğunu söyleriz. Ayrıca bu, matrisin maksimum değerde olduğu anlamına gelir.
- Öte yandan matrisin determinantı 0’a eşitse matris ters çevrilemez. Ve bu durumda bunun tekil veya dejenere bir matris olduğunu söylüyoruz.
Temel olarak herhangi bir matrisi tersine çevirmenin iki yöntemi vardır: determinant yöntemi veya ek matris ve Gauss yöntemi. Aşağıda ilkinin açıklamasını bulacaksınız, ancak aynı zamanda Gauss yöntemiyle bir matrisin nasıl ters çevrileceğini de aşağıya danışabilirsiniz.
Determinant yöntemini kullanarak (veya bitişik matrisi kullanarak) bir matrisi ters çevirin
Bir matrisin tersini hesaplamak için,
![]()
için aşağıdaki formül uygulanmalıdır:
![]()
Altın:
-
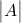
matrisin determinantıdır

-
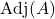
ek matrisidir

- katılımcı
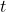
matris aktarımını belirtir, yani eklenen matrisin aktarımı gerekir.
Yorum: Bazı kitaplar biraz farklı bir ters matris formülü kullanır: önce ek matrisi hesaplayıp sonra transpoze etmek yerine, önce A matrisini transpoze eder ve sonra ek matrisini hesaplarlar. Gerçekte sıranın bir önemi yoktur çünkü sonuç tamamen aynıdır. Bunu kullanmayı tercih etmeniz durumunda, değiştirilmiş bir matrisi ters çevirmek için size formülü bırakıyoruz:

Daha sonra örnek olarak bir alıştırmayı çözerek bir matrisin tersini nasıl bulacağımızı göreceğiz:
Determinant yöntemini (veya ek matrisi) kullanarak ters matrisi hesaplama örneği:
- Aşağıdaki matrisin tersini hesaplayın:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
Matrisin tersini belirlemek için aşağıdaki formülü uygulamamız gerekir:
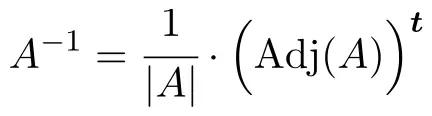
Ancak matrisin determinantı sıfırsa bu, matrisin tersinir olmadığı anlamına gelir. Bu nedenle yapılacak ilk şey matrisin determinantını hesaplamak ve 0’dan farklı olup olmadığını kontrol etmektir:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{vmatrix} = -4- (-6) = 2](https://mathority.org/wp-content/ql-cache/quicklatex.com-710ccd4e4912dd492b496a742eaf7f56_l3.png)
Determinant 0 olmadığı için matris tersinirdir .
Bu nedenle, determinantın değeri formülde yerine konulursa matrisin tersi şöyle olacaktır:
![]()
![]()
Şimdi A’nın yardımcı matrisini hesaplamamız gerekiyor. Bunu yapmak için A matrisinin her bir elemanını onun yardımcısıyla değiştirmeliyiz.
Ekini hesaplamayı unutmayın
![]()
yani satır öğesiyle ilgili
![]()
ve sütun
![]()
için aşağıdaki formül uygulanmalıdır:
![]()
Tamamlayıcı minör nerede
![]()
satırı ortadan kaldıran matrisin determinantıdır
![]()
ve sütun
![]()
.
Böylece, A matrisinin elemanlarının yardımcıları şunlardır:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
![]()
![]()
![]()
![]()
Yorum: 1×1 determinantını mutlak değerle karıştırmayın çünkü 1×1 determinantında sayı pozitife dönüştürülmez.
Temsilciler hesaplandıktan sonra, A’nın yardımcı matrisini bulmak için A’nın elemanlarını yardımcılarıyla değiştirin:
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08fb7666b4518399c2a469ba445762be_l3.png)
Yorum: belirli yerlerde ek matris, burada tanımladığımız ek matrisin devriğidir.
Bu nedenle, ekteki matrisi ters matris formülüne koyarız ve şu hale gelir:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix} ^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0abb4127db9c3c1d0a7b669fbc782605_l3.png)
katılımcı
![]()
Bu bize matrisin transpoze edilmesi gerektiğini söyler. Ve bir matrisin devrikliğini yapmak için satırlarını sütunlara dönüştürmeniz gerekir, yani matrisin ilk satırı matrisin ilk sütunu olur ve ikinci satır da ikinci sütun olur:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & 2 \\[1.1ex] -3 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-22965912cf8aee99610c81cf575c0ecd_l3.png)
Ve son olarak matrisin her terimini şununla çarpıyoruz:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{-1}{2} & \sfrac{2}{2} \\[1.1ex] \sfrac{-3}{2} & \sfrac{4}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-220748840151b429919c7ce6587b1bc0_l3.png)
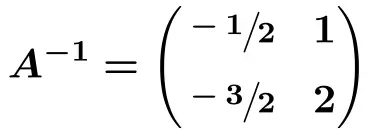
Determinantlar yöntemi (veya bitişik matris) ile ters matrisler üzerine çözülmüş alıştırmalar
1. Egzersiz
Aşağıdaki 2×2 boyut matrisini ek matris yöntemini kullanarak ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfb0807249e78845b375a402eb23a32b_l3.png)
Ters matris formülü şöyledir:
![]()
Önce matrisin determinantını hesaplıyoruz:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{vmatrix} = 7-6 = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c4e3bac90eb0da0361b4be1a2225146_l3.png)
Determinant 0’dan farklı olduğundan matris ters çevrilebilir.
Şimdi A’nın birleşik matrisini hesaplayalım:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dea8fca2c025ff9b7d7673904344996_l3.png)
Matrisin determinantı ve eki hesaplandıktan sonra değerlerini formülde yerine koyarız:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{1} \cdot \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9475e4162eff7e1ed9c08f363a8279ec_l3.png)
Ekteki matrisi transpoze ediyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = 1 \cdot \begin{pmatrix} 7 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5a6aaa8168e55c6eab1e3be1229a3da_l3.png)
A’nın ters matrisi bu nedenle:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{7} & \bm{-3} \\[1.1ex] \bm{-2} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1236ad7262705dbbd9b0a094084ceac5_l3.png)
Alıştırma 2
Determinant yöntemini kullanarak aşağıdaki kare matrisi ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -3 & -2 \\[1.1ex] 5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb735917d200ed35918cd44be6bd155b_l3.png)
Ters matris formülü şöyledir:
![]()
Önce matrisin determinantını hesaplıyoruz:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} -3 & -2 \\[1.1ex] 5 & 4\end{vmatrix} = -12+10 = -2](https://mathority.org/wp-content/ql-cache/quicklatex.com-49cd3daf7c50c811e78c29efe036bda4_l3.png)
Determinant 0’dan farklı olduğundan matris ters çevrilebilir.
Şimdi A’nın birleşik matrisini hesaplayalım:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-208ab7161076485ca6928bd1208f6714_l3.png)
Matrisin determinantı ve eki bulunduktan sonra değerlerini formülde yerine koyarız:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-babecc87455bdc54006a77ba5369e540_l3.png)
Ekteki matrisi transpoze ediyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] -5 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17529597656a112a27d136ca212834d8_l3.png)
Her elemanı şununla çarpıyoruz:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{4}{-2} & \cfrac{2}{-2} \\[3ex] \cfrac{-5}{-2} & \cfrac{-3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be52d2df839244cbb0b0ee00c9e45265_l3.png)
A’nın ters matrisi bu nedenle:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{-2} & \bm{-1} \\[2ex] \cfrac{\bm{5}}{\bm{2}} & \cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13e218c7d075daba3f875345f324d001_l3.png)
Alıştırma 3
Aşağıdaki 3×3 boyutlu matrisi ek matris yöntemini kullanarak ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b6a5f638281754d80983b5a50e15be_l3.png)
Ters matris formülü şöyledir:
![]()
Önce matrisin determinantını Sarrus kuralıyla çözüyoruz:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3 \end{vmatrix} = -24+6-2+16-2+9 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcac1cb3935b1000b6493a2866e8728a_l3.png)
Determinant 0’dan farklı olduğundan matris ters çevrilebilir.
Determinant çözüldükten sonra A’nın birleşik matrisini buluruz:
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4&1\\[1.1ex] 1&-3 \end{vmatrix} = 1 \cdot (-13) = \bm{-13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c510482ac77a8c5d511c095de600f1ba_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 3} = \displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix}1&1\\[1.1ex] 2&-3\end{vmatrix} = -1 \cdot (-5) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa99e03d34c925098c1ad3ed6f06c745_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -2} = \displaystyle (-1)^{1+3} \bm{\cdot} \begin{vmatrix} 1&4\\[1.1ex] 2&1 \end{vmatrix} = 1\cdot (-7) = \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bf9f8565b3e4a99ff254c7558699c13_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3&-2 \\[1.1ex] 1&-3 \end{vmatrix} = -1 \cdot (-7) = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-99e2c3f55fbba7b5faa014758b60f4a8_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 4} = \displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 2&-3 \end{vmatrix} = 1 \cdot (-2) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-23326bccecf752508e7418cbbc8eacd3_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 2&1\end{vmatrix} = -1 \cdot (-4) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9d056af07ce26751783152a67cdedb6_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 3&-2\\[1.1ex] 4&1\end{vmatrix} = 1 \cdot 11 = \bm{11}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bed501806c35c94e491ad2063b2d0653_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 1&1\end{vmatrix} = -1 \cdot 4 = \bm{-4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f108a61eec662b9420708f6920060be_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -3} = \displaystyle (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 1&4 \end{vmatrix} = 1 \cdot 5 = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77a152a00dbb5f1e0f8702dd9511095a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4642a75697fd30286065cdb4063a7bd_l3.png)
Matrisin determinantını ve ekini hesapladıktan sonra değerlerini formülde yerine koyarız:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fae003a07d40b69690566cde77857c3a_l3.png)
Ekteki matrisi transpoze ediyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55717407766afe98f50ca75f20536edc_l3.png)
Ve ters çevrilmiş A matrisi:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \sfrac{\bm{-13}}{\bm{3}} & \sfrac{\bm{7}}{\bm{3}} & \sfrac{\bm{11}}{\bm{3}} \\[1.1ex] \sfrac{\bm{5}}{\bm{3}} & \sfrac{\bm{-2}}{\bm{3}} & \sfrac{\bm{-4}}{\bm{3}} \\[1.1ex] \sfrac{\bm{-7}}{\bm{3}} & \sfrac{\bm{4}}{\bm{3}} & \sfrac{\bm{5}}{\bm{3}}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9835713a5b791ee959d6571d706180f3_l3.png)
Alıştırma 4
Aşağıdaki 3. derece matrisi ek matris yöntemini kullanarak ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bf71320b51e9514d1c372389aeb3410a_l3.png)
Ters matris formülü şöyledir:
![]()
Önce matrisin determinantını hesaplamamız gerekiyor, çünkü determinant 0 ise matrisin tersi yok demektir.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1 \end{vmatrix} = 12+30+8+9-64+5 = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb7dc647f4121450eeadf2f5b62b4475_l3.png)
A’nın determinantı 0 olduğundan matris ters çevrilemez.
Alıştırma 5
Aşağıdaki 3 × 3 kare matrisi determinant matris yöntemiyle ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92e56e0f8013b6b65c0894a139537cae_l3.png)
Ters matris formülü şöyledir:
![]()
Öncelikle matrisin determinantını Sarrus kuralıyla çözüyoruz:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2 \end{vmatrix} = 2+0-12-3-0+16 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-07f116ed906c31644ed0513667988e6f_l3.png)
Determinant 0’dan farklı olduğundan matris ters çevrilebilir.
Determinant çözüldükten sonra A’nın birleşik matrisini buluruz:
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 1 & 0 \\[1.1ex] -2 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-0) = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-20da2eac0d49b1134b39b1f5c95c5659_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 4} = (-1)^{1+2} \bm{\cdot} \begin{vmatrix} -2 & 0 \\[1.1ex] -1 & 2 \end{vmatrix} = -1 \bm{\cdot} (-4-0) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5b80624f0963dfb1a111d96b4e1ceae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -3} = (-1)^{1+3} \bm{\cdot} \begin{vmatrix} -2 & 1 \\[1.1ex] -1 & -2 \end{vmatrix} = 1 \bm{\cdot} \bigl(4-(-1)\bigr) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50dd371e77d1896adb197321b68efd1d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] -2 & 2 \end{vmatrix} = -1 \bm{\cdot} (8-6) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60b779f4366a3ef38ae522fcfca8e7d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -1 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-3) = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-51cb00c42e6932810a4220eb85c61acd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 0} = (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -1 & -2 \end{vmatrix} = -1 \bm{\cdot} \bigl(-2-(-4)\bigr) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b26cbfa55d5567d2dae10c5dfbd158_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -1} = (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] 1 & 0 \end{vmatrix} = 1 \bm{\cdot} \bigl(0-(-3)\bigr) = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d9f1bf4f5e01df910cd59bd4b25f816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -2 & 0 \end{vmatrix} = -1 \cdot (0-6) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ce129b17734facf076e48fb1928d0e1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 2} = (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -2 & 1 \end{vmatrix} = 1 \bm{\cdot} \bigl(1-(-8)\bigr) = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c8b319461dad7880bf2b9f20187b6fb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-748fcb9d9d2a8326379da4d2bd08534a_l3.png)
Matrisin determinantını ve ekini hesapladıktan sonra değerlerini formülde yerine koyarız:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9\end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a0fc0e6effb520e22ff82c3034b4d4c_l3.png)
Ekteki matrisi transpoze ediyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bba6ddbc8ab9f2c64eb03cdb9fea530a_l3.png)
Ve son olarak şunu çalıştırıyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} & \sfrac{3}{3} \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} & \sfrac{6}{3} \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} & \sfrac{9}{3} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f999c23e7d5ce129b410b9f486983e_l3.png)
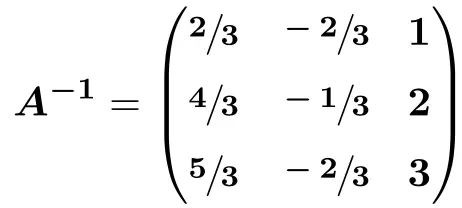
Gauss yöntemini kullanarak bir matrisi ters çevirin:
Gauss yöntemiyle bir matrisin tersini hesaplamak için matrisin satırları üzerinde işlemler yapmanız gerekir (bunu daha sonra göreceğiz). Gauss yönteminin nasıl kullanılacağını görmeden önce matrislerin satırlarında yapılabilecek tüm işlemleri bilmeniz önemlidir:
Gauss yönteminde izin verilen çizgi dönüşümleri
- Matrisin satırlarının sırasını değiştirin .
Örneğin bir matrisin 2. ve 3. satırlarının sırasını değiştirebiliriz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] -2 & 4 & -1 \\[2ex] 6 & 1 & -3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] 6 & 1 & -3 \\[2ex] -2 & 4 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d3f607625afb96bfb250168bd330818_l3.png)
- Bir satırdaki tüm terimleri 0’dan farklı bir sayıyla çarpın veya bölün .
Örneğin 1. satırı 4 ile çarpabilir ve 3. satırı 2’ye bölebiliriz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 1 & -2 & 3 \\[2ex] 3 & -1 & 5 \\[2ex] 2 & -4 & -2 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc} 4 & -8 & 12 \\[2ex] 3 & -1 & 5 \\[2ex] 1 & -2 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cca4df71c23b1f005068a0a93b77dfe_l3.png)
- Bir satırı, aynı satırın toplamı artı başka bir satırın bir sayıyla çarpılmasıyla değiştirin .
Örneğin, aşağıdaki matriste 3. satırı 1 ile çarparak 2. satıra ekliyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 2 & 4 & 1 \\[2ex] 1 & -2 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1\cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 3 & 2 & 4 \\[2ex] 1 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ca6644f015dd42ddbf4ab159bd10dec_l3.png)
Gauss yöntemini kullanarak ters matrisi hesaplama örneği:
Bir matrisi tersine çevirmek için Gauss yönteminin nasıl uygulanacağını bir örnekle görelim:
- Aşağıdaki matrisin tersini hesaplayın:
![Rendered by QuickLaTeX.com \displaystyle A = \left( \begin{array}{ccc} 1 & 0 & 1 \\[2ex] 0 & 2 & 1 \\[2ex] 1 & 5 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-71553480cefa679dcb8eb98d97e0c717_l3.png)
Yapmamız gereken ilk şey A matrisi ile Kimlik matrisini tek bir matriste birleştirmektir. Soldaki A matrisi ve sağdaki Kimlik matrisi:
![]()
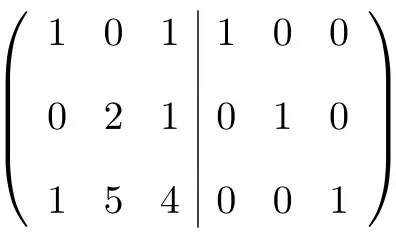
Ters matrisi hesaplamak için soldaki matrisi birim matrise dönüştürmemiz gerekir. Bunu yapmak için de oraya ulaşana kadar satırlara dönüşümler uygulamamız gerekiyor.
Sütunlar halinde ilerleyeceğiz yani satırlar üzerinde işlemler yaparak önce birinci sütundaki sayıları, sonra ikinci sütundaki sayıları ve son olarak da üçüncü sütundaki sayıları dönüştüreceğiz.
Birinci sütundaki 1’ler ve 0’lar zaten uygundur çünkü birim matrisin bu konumlarında da bir 1 ve bir 0 vardır. Bu nedenle bu satırlara şu anda bir dönüşüm uygulamaya gerek yoktur.
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} \color{blue}\boxed{\color{black}1} & 0 & 1 & 1 & 0 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f51b3a869dde9c1697be9e57fce1548_l3.png)
Bununla birlikte, birim matrisin ilk sütununun son elemanında 0 vardır ve artık 1’e sahibiz. Bu nedenle 1’i 0’a dönüştürmemiz gerekir. Bunu yapmak için satır 1’i – ile çarparak satır 3.1’e ekleriz:

Yani eğer bu toplamı yaparsak aşağıdaki matrisi elde ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-992a31603c2182a97d31ddf787df4f06_l3.png)
Böylece 1’i 0’a dönüştürmeyi başardık.
Şimdi sol matrisin ikinci sütununa geçelim. İlk öğe 0’dır ve bu iyidir çünkü birim matrisin aynı konumda 0’ı vardır. Ancak 2 yerine 1 olması gerektiği için ikinci satırı 2’ye bölüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/2}\\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}1} & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a86b61ee601f9cd0ff9a70d1a280f887_l3.png)
Ayrıca ikinci sütunda da 5’i 0’a çevirmemiz gerekiyor. Peki, 5, ikinci satırdaki 1’den beş kat büyük olduğundan, 2. satırı -5 ile çarparak 3. satıra ekleyeceğiz:

Dolayısıyla bu işlemi gerçekleştirerek ikinci sütunun son elemanında 0 bulunan matrisi elde ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 5f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcc790f05d73d308cb7d992841ab031a_l3.png)
Son olarak matrisin son sütununu sola dönüştüreceğiz ancak bu sefer alttan başlamamız gerekiyor. Bu nedenle dönüşümün gerekli olduğu
![]()
1’e. Bu nedenle son satırı 2 ile çarpıyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \color{blue}\boxed{\color{black}1} & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-69614cae4dd388b6454ffd9b8d63c9a5_l3.png)
Artık bunu dönüştürmeliyiz
![]()
son sütunun geri kalanı 0. Ancak bu sefer satırı 2 ile çarpamayız çünkü 1’i de 2’ye çevirmiş oluruz (kimlik matrisinin o konumda 1 olması durumunda). Bu nedenle, 3. satırı -2’ye bölerek 2. satıra ekleyeceğiz:

Yani bu işlemi yaparak dönüştürmeyi başarıyoruz.
![]()
0’da:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \color{blue}\boxed{\color{black}0} & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-537958a51f67c7602ef121fa2c997ca8_l3.png)
Son olarak, üçüncü sütunun ilk satırındaki 1’i 0’a dönüştürmemiz gerekiyor. Üçüncü satırda da aynı sütunda 1 var, dolayısıyla 3. satırı -1 ile çarparak 1. satıra ekleyeceğiz:
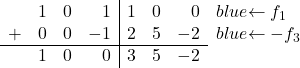
Ve bu işlemi yaparak 1’i 0’a dönüştürmeyi başarıyoruz:
![Rendered by QuickLaTeX.com \ \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 &0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & \color{blue}\boxed{\color{black}0} & 3 & 5 & -2 \\[2ex] 0 & 1 & 0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ddd39df6bc92258ba163c65de4fd59f_l3.png)
Soldaki matrisi başarıyla birim matrise dönüştürdüğümüzde, ters matrisi de biliyoruz. Çünkü ters matris, soldaki matrisi birim matrise dönüştürerek sağ tarafta elde ettiğimiz matristir . Bu nedenle matrisin tersi:
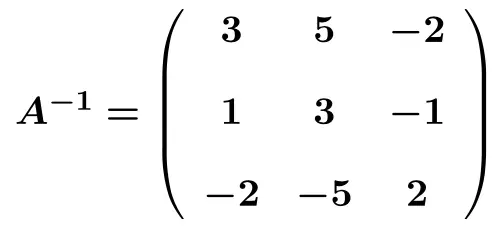
Ters matrisler üzerinde Gauss yöntemiyle çözülmüş alıştırmalar
1. Egzersiz
Aşağıdaki matrisi Gauss yöntemiyle ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36886e1ab1007f9a53bdc0dd71a0d15b_l3.png)
Yapmamız gereken ilk şey A matrisi ile Kimlik matrisini tek bir matriste birleştirmektir. Soldaki A matrisi ve sağdaki birim matrisi:
![]()
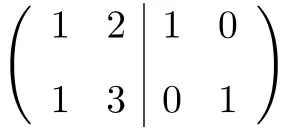
Şimdi ters matrisi hesaplamak için sol taraftaki matrisi birim matrise dönüştürmemiz gerekiyor. Bunu yapmak için de oraya ulaşana kadar satırlara dönüşümler uygulamamız gerekiyor.
İlk terim olan 1 zaten birim matrisle aynıdır. Bu nedenle şu anda ilk satıra dönüşüm uygulamaya gerek yoktur.
Bununla birlikte, birim matrisin ilk sütununun son elemanında 0 vardır ve artık 1’e sahibiz. Bu nedenle 1’i 0’a dönüştürmemiz gerekir. Bunu yapmak için satır 1’i satır 2’den çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc}1 & 2 & 1 & 0 \\[1.5ex] 1 & 3 & 0 & 1\end{array} \right) \begin{array}{c} \\[1.5ex] \xrightarrow{f_2 - f_1} \end{array} \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-247d8605795c43e79b5d7742854cfe6d_l3.png)
İkinci sütuna geçiyoruz: Aşağıdaki 1 iyidir. Ancak yukarıdaki 2 değil çünkü birim matrisin bu konumunda 0 var. Bu nedenle, 2’yi 0’a dönüştürmek için 1. satırdan 2. satırı 2 ile çarparak çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - 2f_2} \\[1.5ex] & \end{array} \left( \begin{array}{cc|cc} 1 & 0 & 3 & -2 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-173a7bdb55ba058e5ae16d1fd8e91564_l3.png)
Ters matris, soldaki matrisi birim matrise dönüştürdükten sonra sağ tarafta elde ettiğimiz matristir. Ve şimdi sol tarafta birim matrisimiz var. Ters matris bu nedenle:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left(} \begin{array}{cc} \bm{3} & \bm{-2} \\[1.5ex] \bm{-1} & \bm{1} \end{array}\bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98896d28465c9e1402e1c443375d93fe_l3.png)
Alıştırma 2
Aşağıdaki matrisi Gauss prosedürüyle ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 1 & -4 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 0 & 1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ae5ba4a92a5ddc00ddf5b11775edafd_l3.png)
Öncelikle A matrisini ve Kimlik matrisini tek bir matrise koyarız:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-81db2ef94d2db597cebb4c0c77685526_l3.png)
Şimdi soldaki matrisi birim matrise dönüştürene kadar satırları dönüştürmemiz gerekiyor.
Sol matrisin ilk sütunu zaten birim matrisin ilk sütunuyla aynıdır. Bu nedenle numaralarından herhangi birini değiştirmeye gerek yoktur.
Bununla birlikte, birim matrisin ikinci sütunun ikinci elemanında 1 vardır ve artık 3 vardır. Bu nedenle 3’ü 1’e dönüştürmeliyiz. Bunu yapmak için 2. satırdan 3. satırı 2 ile çarparak çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & 4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd7cb4d4b81a75038807eb28393a83e_l3.png)
Birim matrisinin ikinci sütununun son elemanında 0 vardır ve artık 1 vardır. Bu nedenle 1’i 0’a dönüştürmeliyiz. Bunu yapmak için 2. satırı 3. satırdan çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-932479e2f574c19ad7906d3d20e52ad0_l3.png)
Birim matrisinin ikinci sütununun ilk elemanında 0 vardır ve artık 1 vardır. Bu nedenle 1’i 0’a dönüştürmeliyiz. Bunu yapmak için 2. satırı 1. satırdan çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-566e1453aab03f9792cb281e4c88a68c_l3.png)
Şimdi tek yapmamız gereken -4’ü 0’a dönüştürmek. Bunu yapmak için 3. satırı 4 ile çarparak 1. satıra ekliyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3\end{array} \right) \begin{array}{c} \xrightarrow{f_1 + 4f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 1 & -5 & 14 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f98a9cabeb101602dd11aa73516b998_l3.png)
Zaten birim matrisi sol taraftan elde etmiştik. Ters matris bu nedenle:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{1} & \bm{-5} & \bm{14} \\[2ex] \bm{0} & \bm{1} & \bm{-2} \\[2ex] \bm{0} & \bm{-1 }& \bm{3} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e43ce6a7061f0339bd5d44b83afec07f_l3.png)
Alıştırma 3
Gauss yöntemini kullanarak aşağıdaki matrisi ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 & 1 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 2 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f02b0186690e68baaa9a630db2c870db_l3.png)
İşleme başlamadan önce A matrisini ve Kimlik matrisini tek bir matrise koymamız gerekiyor:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa6dc5af82076e22b1d0cf7ea16d748b_l3.png)
Şimdi soldaki matrisi satırlar üzerinde işlem yaparak birim matrise dönüştürmeliyiz.
İlk sütunun ilk iki öğesi zaten birim matrisinkilerle aynıdır. Bu nedenle bu rakamların değiştirilmesine gerek yoktur.
Ancak birim matrisin ilk sütununun üçüncü elemanında 0 vardır, burada artık 2 vardır. Bu nedenle 2’yi 0’a dönüştürmeliyiz. Bunu yapmak için 3. satırdan 1. satırı 2 ile çarparak çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 2f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-680a314b8cc900e01886291af12145e4_l3.png)
Birim matrisinin ikinci sütununun ilk elemanında 0 vardır, burada artık 2 vardır. Bu nedenle 2’yi 0’a dönüştürmeliyiz. Bunu yapmak için 1. satırdan 2. satırı 2 ile çarparak çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 -2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f87cbc594287f7ea4938091878562b4c_l3.png)
Birim matrisinin ikinci sütununun son elemanında 0 var, şimdi burada -4 var. Bu nedenle -4’ü 0’a çevirmeliyiz. Bunu yapmak için 2. satırı 4 ile çarparak 3. satıra ekliyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 +4f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8cf2c3878d2d35656953a55bb3baf94_l3.png)
Şimdi tek yapmamız gereken üçüncü sütunun ilk elemanını 0’a dönüştürmek. Bunu yapmak için 3. satırı -1 ile çarparak 1. satıra ekliyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 3 & -6 & -1\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac851b05c2dc25af3d7b9ecc622c9f6_l3.png)
Soldaki matrisin birim matris olduğunu zaten anlamıştık. Yani matrisin tersi
![]()
Doğu:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{3} & \bm{-6} & \bm{-1} \\[2ex] \bm{0} & \bm{1} & \bm{0} \\[2ex] \bm{-2} & \bm{4}& \bm{1} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-161fbe4a4d4dcc4fc503b6e3a9e0bfeb_l3.png)
Alıştırma 4
Gauss yöntemini kullanarak aşağıdaki matrisi ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & -2 & 0 \\[1.1ex] 1 & 2 & 2 \\[1.1ex] 0 & 3 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ad7ccd6aafab72255c96f2bc9148a2_l3.png)
Yapmamız gereken ilk şey A matrisi ile Kimlik matrisini tek bir matriste birleştirmektir:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a832ceb9f09dfa88238c570b46b74d92_l3.png)
Şimdi sol taraftaki matrisi satır işlemlerini uygulayarak birim matrise dönüştürmeliyiz.
İlk sütunun ilk elemanı zaten birim matrisinkiyle aynıdır. Bu nedenle onu değiştirmenize gerek yoktur.
Ancak birim matrisin ilk sütununun ikinci elemanında 0 vardır ve artık 1 vardır. Bu nedenle 1’i 0’a dönüştürmemiz gerekir. Bunu yapmak için 1. satırı 2. satırdan çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83933b5a2315a4dcbc770bf92bf3831b_l3.png)
İkinci sütuna geçiyoruz: İlk önce ikinci satırı 4’e bölerek 4’ü 1’e dönüştürüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/4} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-298984c72a249e2b5c98740cc0c1a11e_l3.png)
Birim matrisinin ikinci sütununun ilk elemanında 0 var, şimdi burada -2 var. Bu nedenle -2’yi 0’a dönüştürmeliyiz. Bunu yapmak için satır 2’yi 2 ile çarparak satır 1’e ekleriz:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \xrightarrow{f_1 +2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dfcdcb586eed87861b3ac0ea46bea2f_l3.png)
Birim matrisinin ikinci sütunun son elemanında 0 vardır, burada artık 3 vardır. Bu nedenle 3’ü 0’a dönüştürmeliyiz. Bunu yapmak için 3. satırdan 2. satırı 3 ile çarparak çıkarırız:
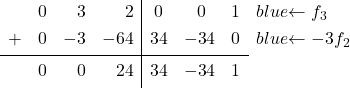
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-94ed5a1b9cf1db0bfb99ce79d0a6d36b_l3.png)
Üçüncü sütuna geçiyoruz: sonuncuyu dönüştürmeliyiz
![]()
1’e dönüştürün. Bunu yapmak için üçüncü satırı 2 ile çarpıyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3 } \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8134938726d3b48fe3d7d789260b128_l3.png)
Kimlik matrisinin son sütununun ikinci elemanında 0 bulunur. Bu nedenle dönüştürmek gerekir
![]()
Bunu yapmak için 2. satırdan 3. satırı 2’ye bölerek çıkarıyoruz:
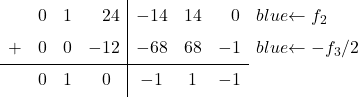
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2 } \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b91b71183a50e41e9be5c7305f8cf3e_l3.png)
Şimdi tek yapmamız gereken üçüncü sütunun ilk elemanını 0’a dönüştürmek. Bunu yapmak için 3. satırı 1. satırdan çıkarıyoruz:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3 } \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -1 & 2 & -2 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2023374b9885dd33fe4d3c12e5a4de59_l3.png)
Ters matris bu nedenle:
![Rendered by QuickLaTeX.com A^{-1}= \left( \begin{array}{ccc} -1 & 2 & -2 \\[2ex] -1 & 1 & -1 \\[2ex] \sfrac{6}{4} &\sfrac{-6}{4} & 2 \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0854e7cb80ba561b6e0c724a9a9b5fff_l3.png)
Son olarak, ters matrisin kesirleri basitleştirilebilir:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{-1} & \bm{2} & \bm{-2} \\[2ex] \bm{-1} & \bm{1} & \bm{-1} \\[2ex] \sfrac{\bm{3}}{\bm{2}} &\sfrac{\bm{-3}}{\bm{2}} & \bm{2} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c7ef6b6cdca2f4a808ed9457bde3b3f_l3.png)
Ters Matris Özellikleri
Ters matris aşağıdaki özelliklere sahiptir:
- Bir matrisin tersi benzersizdir .
- Ters matrisin tersi orijinal matristir:
![]()
- İki matrisin çarpımının tersi , matrislerin terslerinin çarpımına eşittir ancak sıraları değişir.
![]()
- Bir matrisin transpozisyonunu almak ve sonra matrisin tersini yapmak, önce matrisin tersini alıp sonra onu transpoze etmek gibidir.
![]()
- Bir matrisin tersinin determinantını çözmek için matrisin determinantını hesaplayabilir ve ardından bunun tersini yapabiliriz, çünkü iki işlem aynı sonucu verir.
![]()
2×2’lik bir matrisin tersini hızlı bir şekilde hesaplamak için formül
Gördüğümüz gibi herhangi bir matris, determinantlar yöntemiyle veya Gauss yöntemiyle ters çevrilebilir. Ancak ayrı olarak, 2×2’lik bir matrisin tersini çok hızlı bir şekilde bulmak için bir formül de vardır:
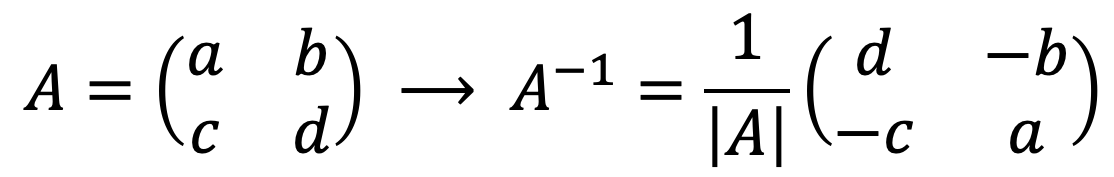
Gördüğünüz gibi 2×2’lik bir matrisi ters çevirmek basittir: sadece matrisin determinantını çözün
![]()
, ana köşegenin elemanlarının konumunu değiştirin ve ikincil köşegenin elemanlarının işaretini değiştirin.
Formülle 2 × 2 ters matrisin nasıl elde edileceğine dair örnek
Aşağıdaki 2 × 2 kare matrisin tersini hesaplayın:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599baee27c05b5610a8714363e1260eb_l3.png)
A matrisinin determinantı:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{vmatrix} & = 3 \cdot (-4)- (-2) \cdot 5 \\ & = -12-(-10) \\[2ex] & =-12+10\\[2ex] &=-2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ab99f7b87d01c670a8598df6364ab58f_l3.png)
Şimdi ters matris formülünü uyguluyoruz:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{-2} \begin{pmatrix} -4 & -5 \\[1.1ex] 2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68fd6e830b576af8abf55be1e11fbafb_l3.png)
Ve matrisi kesirle çarpıyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} =\begin{pmatrix} \cfrac{-4}{-2} & \cfrac{-5}{-2} \\[3ex] \cfrac{2}{-2} & \cfrac{3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41da8ef6bef1d339337717ed4ad86ae5_l3.png)
Bu nedenle ters çevrilmiş matris A şöyledir:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{2} & \cfrac{\bm{5}}{\bm{2}} \\[3ex] \bm{-1} & \bm{-}\cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29da2a64f6da927857de112ca8363ba5_l3.png)
Gördüğünüz gibi bu formülle bir matrisi ters çevirmek çok daha hızlıdır ancak yalnızca 2×2 boyutundaki matrislerde kullanılabilir.
2×2 ters matrislerin formülle çözülmüş alıştırmaları
1. Egzersiz
Aşağıdaki 2×2 boyut matrisini ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc06e21fc1c3c54f9b3fc0dcd4912a8f_l3.png)
A matrisinin determinantı:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{vmatrix} & = 2 \cdot 3- 1 \cdot 5 \\ & = 6-5 \\[2ex] & =1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b0ae510ea7a336cbe5ea56a554da719_l3.png)
Şimdi ters matrisi bulmak için formülü uyguluyoruz:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{1} \begin{pmatrix} 3 & -5 \\[1.1ex] -1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8f18178c829fd38360a04a947d52017_l3.png)
Dolayısıyla A matrisinin tersi şu şekildedir:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{3} & \bm{-5} \\[1.1ex] \bm{-1} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-237fe82cd91972f667f6751fa4735534_l3.png)
Alıştırma 2
Aşağıdaki 2. dereceden matrisin tersini hesaplayın:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f2289d1c5c9aeb87016f719305d900a7_l3.png)
A matrisinin determinantı:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{vmatrix} & = 2 \cdot (-2)- (-1) \cdot 6 \\ & = -4-(-6) \\[2ex] & =-4+6 \\[2ex] & =2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fef2cc00702131123994cc588bf7ea_l3.png)
Şimdi 2×2 boyutunun ters matrisini çözmek için formülü uyguluyoruz:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{2} \begin{pmatrix} -2 & -6 \\[1.1ex] 1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2de7166a0cf59e0f8c5b7750e1947f04_l3.png)
Ve son olarak çarpma işlemini yapıyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{-2}{2} & \cfrac{-6}{2} \\[3ex] \cfrac{1}{2} & \cfrac{2}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6a5973078468914beb4bd4d85a40331_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-1} & \bm{-3} \\[2ex] \cfrac{\bm{1}}{\bm{2}} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a540a077ee9a24da96fa988410aef429_l3.png)
Alıştırma 3
Aşağıdaki 2×2 matrisi ters çevirin:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36e230a808c42411a9cfd2d9eb44543d_l3.png)
A matrisinin determinantı:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 4 & 1 \\[1.1ex] 5 & 2\end{vmatrix} & = 4 \cdot 2 - 5 \cdot 1 \\ & = 8-5 \\[2ex] & =3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e7a6c5ef316ae51b43c90863c6245780_l3.png)
Şimdi 2×2 boyutunun ters matrisini hesaplamak için formülü uyguluyoruz:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{3} \begin{pmatrix} 2 & -1 \\[1.1ex] -5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2f359bd166c295b869a8cf04d927097_l3.png)
Ve son olarak kesir ile matris arasındaki çarpımı yapıyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{\bm{2}}{\bm{3}} & \bm{-}\cfrac{\bm{1}}{\bm{3}} \\[3ex] \bm{-}\cfrac{\bm{5}}{\bm{3}} & \cfrac{\bm{4}}{\bm{3}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a02ea2e547dcc21081ae80df407a4e0_l3.png)
Alıştırma 4
Aşağıdaki ikinci dereceden matrisin tersini bulun:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-422fcd6f391a2682e4b546c9e9c05b55_l3.png)
A matrisinin determinantı:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{vmatrix} & = (-2) \cdot 10- (-3) \cdot 5 \\ & = -20-(-15) \\[2ex] & =-20+15 \\[2ex] & =-5\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e9997751e16d3b976454be828cb914d_l3.png)
Şimdi 2×2 boyutunun ters matrisini oluşturmak için formülü uyguluyoruz:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{-5} \begin{pmatrix} 10 & -5 \\[1.1ex] 3 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c0c614039614bd9125b2920da8698eb_l3.png)
Ve son olarak çarpma işlemini yapıyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{10}{-5} & \cfrac{-5}{-5} \\[3ex] \cfrac{3}{-5} & \cfrac{-2}{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb1dfc870b3045eaefc1716a80e2ca2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-2} & \bm{1} \\[2ex] \bm{-}\cfrac{\bm{3}}{\bm{5}} & \cfrac{\bm{2}}{\bm{5}} \ \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c49e161c701254cfbe20353c11980eb_l3.png)
Ters matrisli bir denklem sistemini çözme
Bir matrisin tersinin gerçek uygulamalarını değerlendirmek zordur. Aslında muhtemelen merak ediyorsunuzdur… ters matris ne için kullanılır? Gerçekten herhangi bir şey için kullanılıyor mu?
Ters matrisin kullanımlarından biri de doğrusal denklem sistemlerini çözmektir . Ve evet, birbirinden çok farklı iki kavram gibi görünseler de, bir matrisin tersini alarak bir denklem sisteminin çözümünü bulmak mümkün.
Bunun nasıl yapıldığını bir örnekle görelim:
- Aşağıdaki denklem sisteminin çözümünü ters matrisle hesaplayın:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+3y=5 \\[2ex] 2x+4y=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-200c0f994f86752e7d650621a0d4100f_l3.png)
Her şeyden önce, bir denklem sisteminin matrisler biçiminde ifade edilebileceği gözlenmelidir:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\begin{pmatrix} x \\[1.1ex]y \end{pmatrix} = \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b9c9f181fc16a501799145c516a9747_l3.png)
Sistemin bu matris formunun denklemli ifadeye eşdeğer olduğunu doğrulayabiliriz: Matrisleri çarparsak sistemin iki denklemini elde ettiğimizi görürüz.
Şimdi sonraki adımları basitleştirmek için şunu arayacağız:
![]()
bilinmeyenlerin katsayılarını içeren matrise,
![]()
bilinmeyenleri içeren matris sütunlarına ve
![]()
bağımsız terimlerle sütun matrisine:
![]()
Yani matris
![]()
matris denkleminin bilinmeyenidir.
Bu matris denklemini çözmek için burada çok detaylı anlatmayacağımız bir prosedürü izlemelisiniz. Tamamen anlamak istiyorsanız tüm süreci adım adım anlattığımız matrislerle denklem çözümü nasıl yapılır konusuna göz atabilirsiniz.
Bu prosedür, ters matrislerin bir özelliğine dayanmaktadır: herhangi bir matrisin tersiyle çarpılması, Kimlik (veya Birim) matrisine eşittir. Bu nedenle bilinmeyen matris kolaylıkla çözülebilir.
![]()
denklemin her iki tarafını A matrisinin tersiyle çarparak:
![]()
![]()
![]()
![]()
Ve matrisi izole ettiğimizde
![]()
tersini hesaplıyoruz
![]()
ve matrislerin çarpımını çözüyoruz:
![Rendered by QuickLaTeX.com \displaystyle X=\left.\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\right.^{-1}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a1290e37a9e3f56fc6b288bc7686d66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X=\cfrac{1}{-2} \begin{pmatrix} 4 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21471fc8a4c04aac3121519e8ef874e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X= \begin{pmatrix} -1 \\[1.1ex] 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9457fedf68c4bdfea898922e465eeb8_l3.png)
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()