Tekil veya dejenere matris

Bu sayfada bir matrisin tekil veya dejenere olmasının ne anlama geldiğini göreceksiniz. Ayrıca şüphe duymamanız için size birkaç örnek gösteriyoruz ve son olarak bu tür matrislerin tüm özelliklerini açıklıyoruz.

Tekil veya dejenere matris nedir?

Dejenere matris olarak da adlandırılan tekil matrisin tanımı aşağıdaki gibidir:

Tekil veya dejenere bir matris, ters çevrilemeyen bir kare matristir ve bu nedenle determinantı 0’a eşittir.

Bu nedenle, bir matrisin ne zaman tekil olduğunu bilmek için determinantını hesaplamanız yeterlidir: sonuç 0 ise matris tekildir, diğer taraftan determinant 0’dan farklıysa matris tekil değildir .

Ters matris hakkında daha fazla bilgi edinmek istiyorsanız, Gauss yöntemini kullanarak bir matrisin nasıl ters çevrileceğinin ayrıntılı olarak açıklandığı bu sayfaya başvurabilirsiniz, ayrıca uygulamaya yönelik adım adım çözülmüş birkaç örnek ve alıştırma bulacaksınız.

Öte yandan tekil matrislere düzenli olmayan matrisler de denir çünkü bunlar normal matrisin tam tersini ifade eder.

Tekil matris örnekleri

Tekil veya dejenere matrisin açıklamasını gördükten sonra, birkaç boyutlu tekil matrislerin bazı örneklerini görelim:

2×2 tekil matris örneği

2x2 boyutunda tekil veya dejenere matris örneği

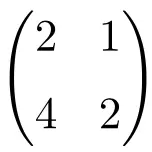
Determinantını hesaplayarak bunun tekil bir matris olduğunu kolayca doğrulayabiliriz:

$\displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}$

2. mertebeden matrisin determinantı 0’a eşit olduğundan tekil bir matristir.

3 × 3 tekil matris örneği

3x3 boyutunda tekil veya dejenere matris örneği

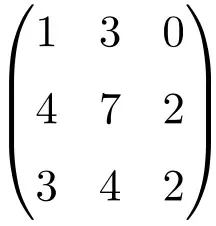
Tersine çevrilemeyen bir matris olduğunu doğrulamak için matrisin determinantını çözmeliyiz:

$\displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}$

3. mertebeden matrisin determinantı 0 verir, dolayısıyla tekil bir matristir.

4 × 4 tekil matris örneği

4x4 boyutunda tekil veya dejenere matris örneği

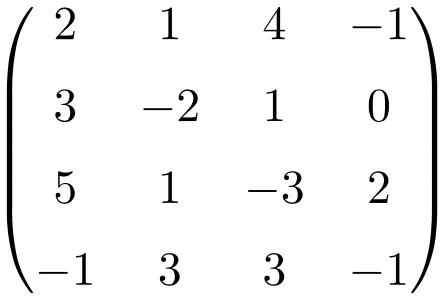
Matrisin determinantını yaparak onun tekil bir matris olduğunu gösteririz:

$\displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}$

4. mertebeden matrisin determinantı sıfır olduğundan ters matrisi mevcut değildir.

Uyarı: Eğer determinant hesaplamaları konusunda şüpheleriniz varsa determinant nasıl hesaplanır sayfasına bakabilirsiniz.

Tekil matrislerin özellikleri

Bu tür matrislerin özellikleri aşağıdaki gibidir:

Tekil bir matrisin en az iki sütunu veya iki satırı doğrusal kombinasyonlardır ve doğrusaldır, dolayısıyla bağımlıdır.

Sıfırlarla dolu bir satır veya sütun içeren herhangi bir matris tekil bir matristir.

Tekil veya dejenere bir matrisin rütbesi boyutundan küçüktür.

Tekil bir matrisin matris çarpımı başka bir matrisle çarpıldığında başka bir tekil matris elde edilir. Bu durum belirleyicilerin özelliklerinden çıkarılabilir:

$\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)=0 \cdot \text{det}(B) = 0$

Benzer şekilde, tekil bir matrisin gücü, yükseltildiği güce bakılmaksızın başka bir tekil matrise eşittir.

Tekil bir matrisin devriği, başka bir tekil matrisin ortaya çıkmasına neden olur, çünkü aktarılmış (veya aktarılmış) bir matrisin determinantı, aktarılmamış matrisin determinantına eşdeğerdir:

$\text{det}(A^t) = \text{det}(A)=0$

Tekil bir matrisin bir skalerle çarpılması onun dejenere matris olma durumunu değiştirmez.

Tekil bir matrisin eki de tekildir.

Üçgen matrisler ve köşegen matrisler, ana köşegenlerinin en az bir elemanı sıfırsa dejenere matrislerdir.

Açıkçası, sıfır matrisi tekil bir matristir.

Aynı şekilde üstelsıfır bir matris de tekil bir matristir.

Tekil bir matrisle ilişkili bir doğrusal denklem sisteminin çözümü yoktur veya sonsuz sayıda çözümü vardır.

Son olarak, bir kare matris ancak ve ancak 0’a eşit en az bir özdeğere (veya özdeğere) sahipse tekildir.