Bu sayfada bir tek terimlinin parçalarının ne olduğunu (katsayı, gerçek kısım, derece vb.) ve bunları nasıl kolayca tanımlayabileceğimizi açıklıyoruz. Ayrıca örnekleri görebilecek ve hatta bir monomiyalin bölümleri üzerinde adım adım çözülen alıştırmalarla pratik yapabileceksiniz.
Bir monomiyalin parçaları nelerdir?
Bir monomialin parçaları şunlardır:
- Katsayı : Monomiyalin değişkenlerini (veya harflerini) çarpan sayıdır.
- Değişken : Tek terimde görünen harflerin her biri.
- Değişmez kısım : tüm üsleriyle birlikte monomial oluşturan tüm değişkenlere karşılık gelir.
- Derece : Tek terimli değişkenlerin tüm üslerinin toplamıdır.
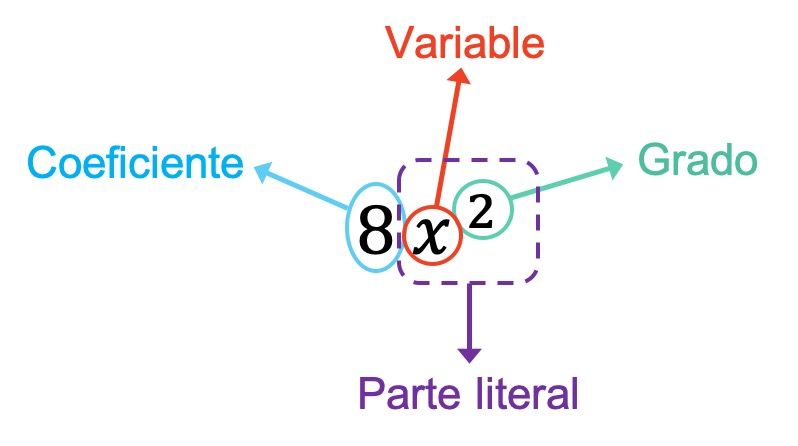
Önceki örnekte gördüğünüz gibi değişkenleri çarpan sayı olduğu için monomialin katsayısı 8’dir. Ayrıca bu durumda tek terimlinin yalnızca bir değişkeni vardır, o da x’tir. Bu nedenle, monomun gerçek kısmı bu değişken artı üssünden, yani x 2’den oluşur. Ve son olarak, tek terimli ikinci derecedendir çünkü sahip olduğu tek üs 2’dir.
Öte yandan, bir tek terimlinin parçalarının özelliklerinden biri, iki tek terimlinin aynı gerçek parçaya sahip olması durumunda, bunların benzer tek terimli olduğunun söylenmesidir. Bu tür tek terimlilerle ilgili daha fazla bilgiyi, diğer şeylerin yanı sıra matematik için neden bu kadar önemli olduklarının açıklandığı bağlantılı sayfada bulabilirsiniz.
Tek terimlilerin parçalarına örnekler
Tek terimlinin parçaları kavramını tam olarak anlamanız için size birkaç örnek bırakıyoruz:
örnek 1
![]()
- Monom katsayısı:
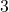
- Tek terimli değişkenler:
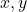
(bu durumda iki değişken vardır)
- Monomiyalin değişmez kısmı:
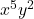
- Monomiyalin derecesi:
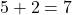
Örnek 2
![]()
- Monom katsayısı:
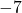
- Tek terimli değişkenler:
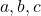
(bu durumda üç değişken vardır)
- Monomiyalin değişmez kısmı:
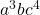
- Monomiyalin derecesi:
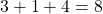
Bir değişkenin üssü belirlenmediğinde bunun bire yükseltildiği anlamına geldiğini ve dolayısıyla gerçekte o değişkenin üssünün 0 değil 1 olduğunu unutmayın. Bu nedenle hesaplamaya bir birim ekledik. bu tek terimlinin derecesi (3+ 1 +4=8), çünkü
![]()
Daha fazla ilgileniyorsanız, aşağıdaki bağlantıda daha fazla tek terimli örnek görebilirsiniz. Ek olarak, farklı türde tek terimlilerin var olduğunu, bir tek terimlinin sayısal değerinin nasıl hesaplandığını ve bir tek terimli ile bir polinom arasındaki farkın ne olduğunu görebileceksiniz.
Tek terimlilerin parçalarının çözülmüş problemleri
Son olarak, bir tek terimlinin parçalarının farklı tanımlarını anlayıp anlamadığınızı kontrol edebilmeniz için size birkaç alıştırma sunuyoruz.
1. Egzersiz
Aşağıdaki tek terimlinin tüm parçaları nelerdir?
![]()
Monom katsayısı:
![]()
Tek terimli değişkenler:
![]()
Monomiyalin değişmez kısmı:
![]()
Monomiyalin derecesi:
![]()
Alıştırma 2
Aşağıdaki monomialin tüm elemanlarını tanımlayın:
![]()
Monom katsayısı:
![]()
Tek terimli değişkenler:
![]()
Monomiyalin değişmez kısmı:
![]()
Monomiyalin derecesi:
![]()
Alıştırma 3
Aşağıdaki monomialin parçalarını kesirli olarak belirleyin:
![]()
Monom katsayısı:
![]()
Tek terimli değişkenler:
![]()
Monomiyalin değişmez kısmı:
![]()
Monomiyalin derecesi:
![]()
Mükemmel! Eğer bu noktaya kadar geldiyseniz, muhtemelen bir tek terimlinin bölümleri hakkındaki her şeyi zaten anlamışsınızdır. İşte bu yüzden bunu bir sonraki seviyeye taşımaya vetek terimlilerle nasıl işlem yapılacağını öğrenmeye hazırsınız. Burada sadece tek terimli var olan tüm işlem türlerinin nasıl hesaplandığını görmekle kalmayacak, aynı zamanda tek terimli birleşik işlemlerin nasıl çözüleceğini de görecek ve çözülmüş alıştırmalarla adım adım pratik yapabileceksiniz.