Tartaglia (veya Pascal) üçgeni

Bu sayfada Pascal üçgeni olarak da adlandırılan Tartaglia üçgeninin ne olduğunu açıklıyoruz. Tartaglia (veya Pascal) üçgeninin matematiksel olarak nasıl oluşturulacağını, ne için kullanıldığını ve tüm özelliklerinin neler olduğunu öğreniyoruz. Son olarak bu çok önemli üçgenin nasıl ve ne zaman ortaya çıktığını gösteriyoruz.

Tartaglia’nın (veya Pascal’ın) üçgeni nedir?

Pascal üçgeni olarak da adlandırılan Tartaglia üçgeni , sıralı tam sayıların üçgen biçiminde matematiksel bir temsilidir. Tartaglia (veya Pascal) üçgeni matematiksel hesaplamalar yapmak için kullanılır.

Bu Tartaglia veya Pascal üçgeninin tanımıdır, ancak kavramı üçgenin görüntüsüyle daha iyi anlayacağınız kesindir:

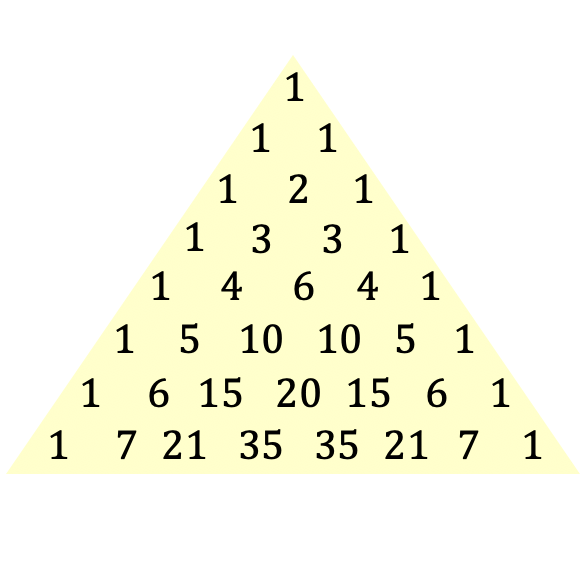
Tartaglia üçgeni, bu üçgen ifadesini 1654 yılında ortaya koyan Fransız filozof ve matematikçi Blaise Pascal’ın anısına Pascal üçgeni olarak da adlandırılmaktadır, ancak bu üçgen çok eski çağlardan beri bilinmektedir. Aşağıda bu özel üçgenin tarihini inceleyeceğiz.

Tartaglia veya Pascal üçgeni nasıl inşa edilir?

Pascal üçgeninde (veya Tartaglia’da) gördüğünüz gibi, çok sayıda sayı var, ancak bu onları ezberlememiz gerektiği anlamına gelmiyor (çok şükür). Pascal veya Tartaglia üçgenindeki tüm sayıları kolayca bulmanızı sağlayan bir formül var, sadece basit toplamları çözmeniz yeterli.

Tartaglia veya Pascal üçgenini oluşturmak için üçgenin tepesinden başlarsınız ki bu her zaman 1’dir ve ardından aşağıdaki çizgiler hesaplanır. Aşağıdaki satırlardaki her sayı, her zaman 1 olan satırların uçları hariç, hemen üstündeki iki sayının toplamıdır.

Dolayısıyla Tartaglia üçgeninin istediğiniz kadar satırını hesaplayabilirsiniz çünkü sayıları toplayarak satırları art arda ekleyebilirsiniz.

Tartaglia veya Pascal üçgeni ne için kullanılır?

Tartaglia üçgeninin nasıl inşa edileceğini bilmek çok iyi ama… bu aritmetik üçgen ne için kullanılıyor? Tartaglia’nın (veya Pascal’ın) üçgeninin matematikte, özellikle cebir alanında birçok uygulaması vardır.

kombinatoryal sayılar

Her şeyden önce Tartaglia üçgeni, binom katsayıları olarak da adlandırılan kombinatoryal sayıları doğrudan hesaplamak için kullanılır. Bu tür operasyonların ne olduğunu bilmiyorsanız web sitemizden araştırabilirsiniz (sağ üstte arama motorumuz var) çünkü bunların nasıl çözümlendiğini anlattığımız detaylı bir yazı yazdık ve işte buradasınız. Ayrıca adım adım çözülen örnekler ve alıştırmalar da bulacaksınız. Ancak özet olarak bir kombinatoryal sayının cebirsel ifadesi aşağıdaki gibidir:

$\displaystyle \begin{pmatrix} n \\ k \end{pmatrix}$

Tartaglia üçgeni ile tüm kombinatoryal sayılar kolayca belirlenebilir, çünkü her bir binom katsayısının çözümü, aşağıdaki şekilde gösterildiği gibi bu üçgensel ifadenin bir numarasına eşdeğerdir:

Tartaglia veya Pascal üçgeninin kombinatoryal sayıları

Örneğin, kombinatoryal sayı

$\displaystyle \begin{pmatrix} 4 \\ 2 \end{pmatrix}$

6 değerini döndürür çünkü Tartaglia üçgeninde bunun yerine 6 vardır.

Dolayısıyla, Tartaglia veya Pascal üçgenini nasıl oluşturacağınızı biliyorsanız, herhangi bir kombinatoryal sayıyı formüllerini kullanmadan hızlı bir şekilde hesaplayabilirsiniz.

Newton’un iki terimlisi

Tartaglia (veya Pascal) üçgeninin bir başka kullanımı da binomların kuvvetlerini hesaplayabilmektir (binomun ne olduğunu öğrenmek için bu bağlantıya tıklayın).

Bir binomun potansiyelleştirilmesine bir örnek, aşağıdaki gibi dikkate değer kimliklerdir:

$(a+b)^2$

Dikkat çekici özdeşlikler matematik için çok önemlidir çünkü birçok hesaplamayı kaydetmemize ve karmaşık işlemleri doğrudan ve hızlı bir şekilde çözmemize olanak tanırlar. Bu nedenle , Önemli Kimliklerin ne olduğunu hâlâ bilmiyorsanız aşağıdaki bağlantıya göz atmanızı öneririz.

Bir önceki linkte gördüğünüz gibi dikkat çeken ürünler doğrudan formülleriyle çözülebiliyor. Ama… çift küpe veya daha yüksek bir dereceye yükseltildiğinde ne olur?

$\begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}$

Peki, bu binomlar, binom teoremi (veya Newton’un binomunu) sayesinde Tartaglia üçgeni ile çok basit bir şekilde hesaplanabilir. Bir kez bu yönteme hakim olmanıza rağmen uygulaması hızlıdır, iyi bir şekilde açıklamak için bir sayfanın tamamına ihtiyacınız vardır. Bu tür binomların nasıl çözüleceğiyle daha fazla ilgileniyorsanız, bağlantılı sayfaya tıklayın ve nasıl yapıldığını görebilirsiniz.

Kombinatorik

Kombinasyonları ve olasılıkları belirlemek için Tartaglia üçgeni veya Pascal üçgeni de kullanılabilir.

Bir gruptan sıralamaya bakılmaksızın kaç farklı grup oluşturulabileceğini belirlememiz gereken bir sorunla karşılaşırsak Tartaglia üçgenini kullanabiliriz.

Örneğin, 5 kartımız varsa, 3’ü kaç şekilde seçebileceğimizi bilmek için Tartaglia üçgeninin beşinci satırının (ilk satır aynı zamanda 0’dır) üçüncü sütununa (ilk sütun sıfırdır) gitmeniz yeterlidir. Bu konumdaki sayı (10), 3 kartın seçilebileceği olasılıkların sayısına karşılık gelir.

$1 \quad 5 \quad 10 \quad \color{blue}\boxed{ \color{black}10} \color{black} \quad 5 \quad 1$

Yani 5 karttan 3’er karttan oluşan 10 farklı grup oluşturulabilir.

Tartaglia veya Pascal üçgeninin özellikleri

Pascal üçgeni olarak da adlandırılan Tartaglia üçgeni aşağıdaki özelliklere sahiptir:

Tartaglia (veya Pascal) üçgeni simetriktir, yani üçgenin tamamını iki eşit eşkenar üçgene bölen dikey çizgi bir simetri eksenidir.

Pascal üçgeninin herhangi bir satırındaki tüm sayıların yatay toplamı 2’nin kuvvetine eşittir.

tartaglia veya pascal üçgeninin özellikleri

Tartaglia üçgeninin köşegenleri de önemlidir: ilk köşegendeki (dış köşegen) sayılar birdir, ikinci köşegen tüm doğal sayıların dizisinden oluşur, üçüncü köşegen üçgen sayılara karşılık gelir ve dördüncü köşegen oluşur. dörtgen (veya dört yüzlü) sayıların.

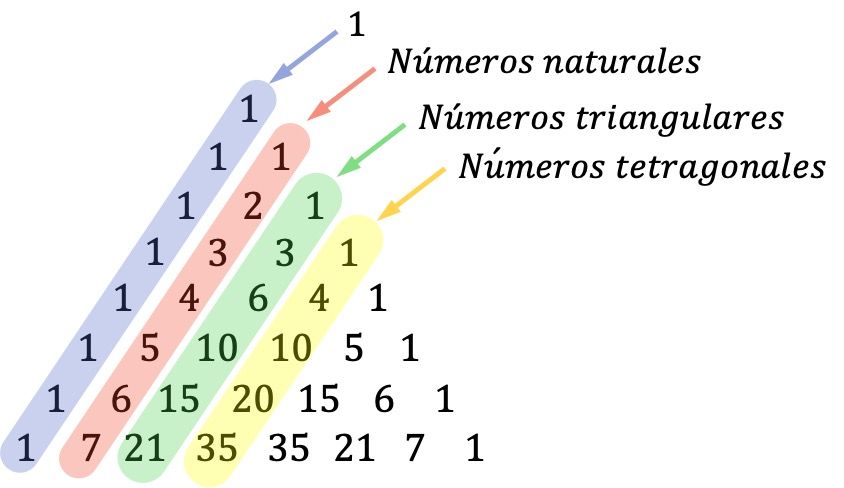
tartaglia üçgeni veya Pascal üçgeni ve dörtgen sayıları

Üçgen sayılar üçgen şeklinde gösterilebilen sayılardır. Ve dörtgen sayılar üçgen piramitler oluşturan sayılardır.

Üçgen veya dörtgen sayıların ne olduğunu bilmiyorsanız hiçbir şey olmaz, bu sadece Tartaglia üçgeniyle ilgili bir meraktır. Ancak doğal sayıların (elementleri saymak için kullanılan sayılar) anlamını bilmeniz gerekir.

1 sayısı hariç, bir satırdaki ilk sayı asal sayı ise aynı satırdaki tüm sayılar o sayıya bölünür. Örneğin sekizinci sırada (1-7-21-35-35-21-7-1) 7, 21 ve 35 sayıları 7’ye bölünebilir (yedi asal sayıdır).

Tartaglia üçgeninin bir diğer özelliği de köşegenlerin belirli bir şekilde toplanmasıyla Fibonacci serisinin bulunabilmesidir:

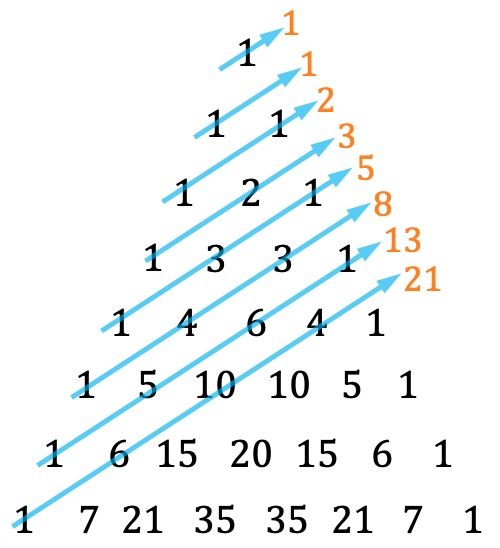
tartaglia veya pascal üçgeni fibonacci serisi

Fibonacci dizisinin her teriminin önceki iki terimin toplamına eşit olduğunu unutmayın; ilk iki terim 1 ve 1’dir. Dolayısıyla Fibonacci dizisine ait sayılar şunlardır: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144, 233,…

Pascal üçgeninin üçüncü köşegeninden (1-3-6-10-15-…) ardışık iki sayıyı toplarsak tam kareyi (1, 4, 9, 16, 25,…) elde ederiz.

Pascal üçgeninin çift sayılarını bir renge, tek sayılarını ise başka bir renge boyarsak ünlü bir geometrik dizi olan Sierpinski üçgeninin şeklini elde ederiz. Aşağıda tek sayıların siyah, çift sayıların ise beyaz renkte olduğu, yüksekliği 512 olan Pascal üçgenini görüyorsunuz:

tataglia'nın sierpinski üçgeni veya pascal üçgeni

Singmaster varsayımı, 1’den büyük her sayının oluşma sayısının sonlu olduğunu söylüyor. Veya başka bir deyişle Tartaglia üçgenindeki satır sayısı sonsuz olmasına rağmen, 1 dışındaki her sayının görünme sayısı sonludur. İlginç bir şekilde, 3003 sayısı bugüne kadar üçgende sekiz defaya kadar göründüğü bilinen tek sayıdır.

Tartaglia veya Pascal üçgeninin tarihi

Artık Tartaglia üçgeninin neye benzediğini bildiğimize göre, bu çok özel matematiksel üçgenin ne zaman icat edildiğine bakalım.

Aritmetik üçgenin adı esas olarak ünlü bilim adamları Tartaglia ve Pascal’a atfedilse de bu cebirsel üçgen daha önce de kullanılıyordu.

Binom katsayılarından oluşan bir üçgenin ilk kaydı Hindistan’da 10. yüzyıldan kalmadır. Ancak Persler, özellikle matematikçiler Al-Karaji (953-1029) ve Omar Hayyam (1048-1131) başta olmak üzere, onun özelliklerini incelemeye başladılar. Bu nedenle İran’da Hayyam-Pascal üçgeni veya hatta sadece Hayyam üçgeni olarak popüler hale getirildi.

Bu üçgen Çin’e 11. yüzyılda matematikçi Jia Xian tarafından tanıtılmaya başlandı, ancak daha sonra 13. yüzyılda Yang Hui onu aritmetik üçgen olarak tanıttı. Ve bu nedenle Asya ülkesinde buna Yang Hui üçgeni deniyor.

Matematiksel üçgen daha sonra Alman Petrus Apianus’un 1527 yılında Rehnung adlı kitabında yayımlanmasıyla Avrupa kıtasına ulaştı. Buradan yola çıkarak ünlü İtalyan cebirci Niccolò Fontana Tartaglia, 16. yüzyılın ilk yarısında üçgeni derinlemesine inceledi ve İtalya gibi ülkelerde onun onuruna Tartaglia üçgeni olarak biliniyor.

Son olarak, Fransız Blaise Pascal, 1654’te Aritmetik Üçgen Üzerine İnceleme adlı yayınında incelenen üçgenin birçok özelliğini gösterdi; dolayısıyla Pascal üçgeni adı verildi. Bu özelliklerden bazılarının zaten bilindiğini belirtmek gerekir, ancak bunların gösterimini matematiksel tümevarımla gerçekleştiren Pascal’dı.

Tartaglia'nın (veya pascal'ın) üçgeni