▷ Bir fonksiyonun sürekli olup olmadığı nasıl anlaşılır (çözümlü alıştırmalar)

Bu yazıda sürekli fonksiyonların ne olduğunu ve bir fonksiyonun bir noktada sürekli olup olmadığının nasıl belirleneceğini açıklıyoruz. Ek olarak sürekli fonksiyonların özelliklerini ve en yaygın fonksiyonların süreklilik analizini bulacaksınız. Son olarak, kavramı tam olarak anlamak için sürekli fonksiyonla ilgili çözümlü alıştırmalar yapabilirsiniz.

Sürekli fonksiyon nedir?

Bir fonksiyonun sürekliliği grafiksel olarak incelenebilir. Sürekli fonksiyon, kalemi kağıttan çıkarmadan grafik üzerinde gösterilebilen bir fonksiyondur.

Sürekli işlev

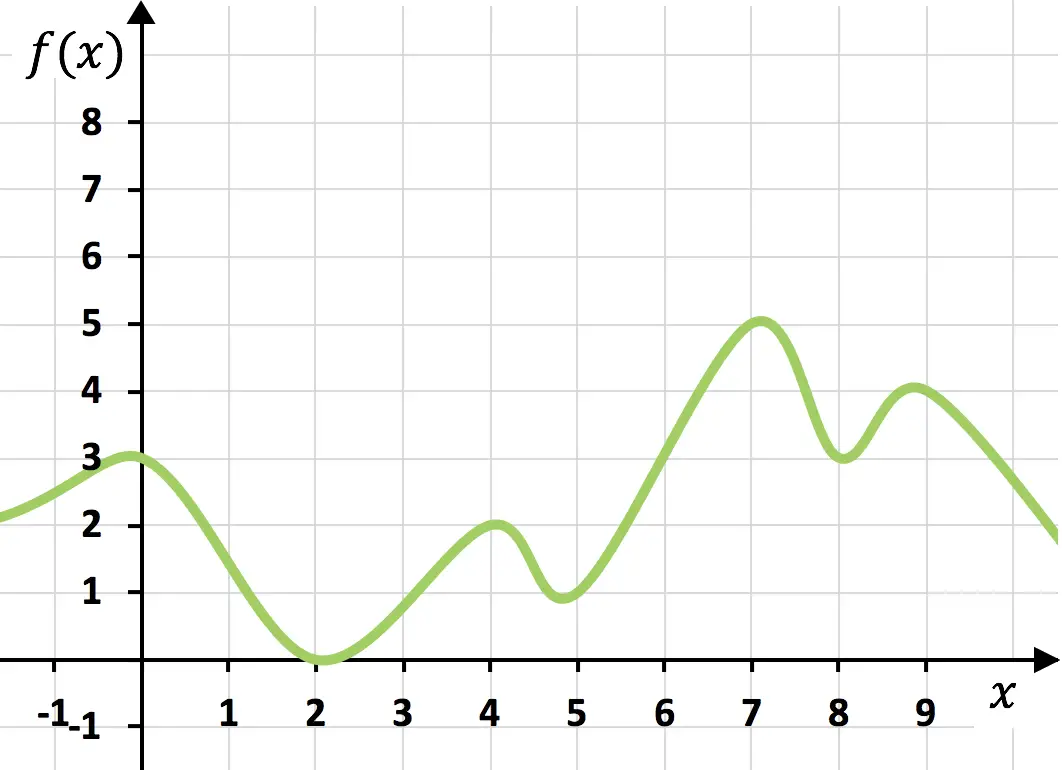
Yukarıdaki fonksiyon süreklidir çünkü elinizi kağıttan kaldırmadan tek vuruşta çizilebilir.

Öte yandan bir fonksiyona önceki süreklilik koşulu konulmadığında buna süreksiz fonksiyon denir.

Süreksiz fonksiyon

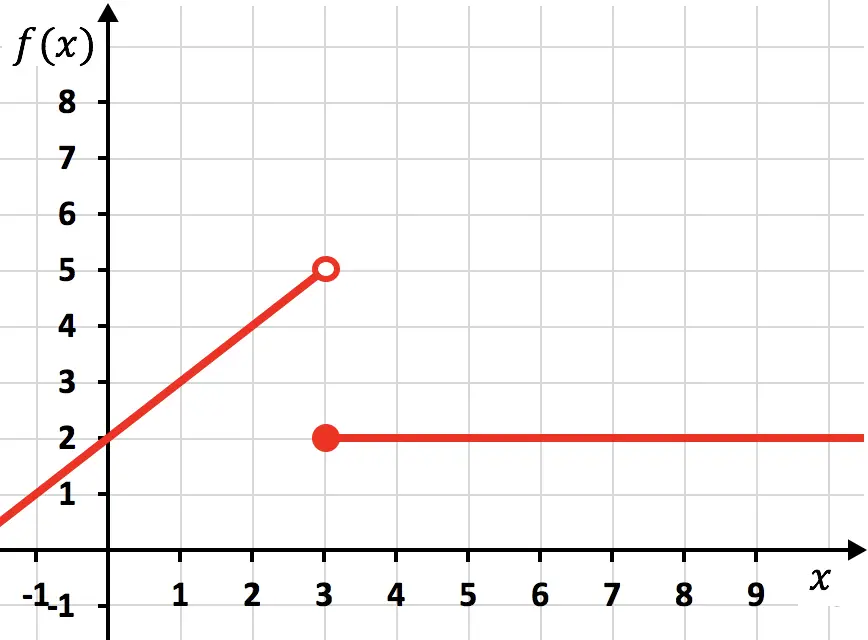
Önceki fonksiyon süreksizdir çünkü onu temsil etmek için kalemle iki çizgi çizmeniz gerekir. Bu durumda fonksiyon x=3’te sürekli olmaktan çıkar, dolayısıyla x=3’ün bir süreksizlik noktası olduğunu söyleriz.

Ek olarak üç tür süreksizlik vardır: önlenebilir süreksizlik, kaçınılmaz sonlu atlama süreksizliği ve kaçınılmaz sonsuz atlama süreksizliği. Aşağıdaki bağlantıda her bir süreksizlik türünün neye benzediğini ve her birinde neyin farklı olduğunu görebilirsiniz:

➤ Bakınız: süreksizlik türleri

Bir fonksiyonun bir noktada sürekliliği

Sürekli bir fonksiyonun grafiğinin neye benzediğini gördükten sonra, bir fonksiyonun sürekli olup olmadığını analitik olarak nasıl anlayacağımıza bakacağız.

Matematiksel olarak bir fonksiyon, aşağıdaki üç koşulun karşılanması durumunda bir noktada süreklidir:

Bu noktada fonksiyon mevcuttur yani noktanın görüntüsü mevcuttur.

$\exists \ f(a)$

Bu noktada fonksiyonun sınırı var. Dolayısıyla fonksiyonun bu noktadaki sol ve sağ yanal limitleri eşittir.

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

Noktanın görüntüsü bu noktadaki fonksiyonun limitiyle çakışmaktadır.

$\displaystyle f(a)=\lim_{x \to a} f(x)$

Yani bir fonksiyonun her noktasında üç süreklilik koşulu karşılanıyorsa fonksiyon süreklidir.

Örnek olarak aşağıdaki parçalı fonksiyonun sürekliliğini analiz edeceğiz:

parçalı tanımlanmış bir fonksiyonun sürekliliği

Bölümleri değiştirseniz bile, bu noktada

$x=-2$

Fonksiyonun bu noktadaki yanal sınırları eşit olduğundan ve fonksiyonun bu noktadaki değerine daha fazla örtüştüğünden fonksiyon süreklidir.

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

Diğer taraftan fonksiyon bu noktada sürekli değildir.

$x=4$

çünkü iki yanal limit farklıdır ve dolayısıyla fonksiyonun limiti bu noktada mevcut değildir:

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

Kısacası parçalarla tanımlanan fonksiyon, reel sayılar hariç tüm reel sayılarda süreklidir.

$x=4,$

bir süreksizliğin olduğu yer.

Ayrıca fonksiyonun süreksiz olduğunu da doğrulayabiliriz.

$x=4$

çünkü bunu grafiksel olarak göstermek için bu noktada kalemi kağıttan çıkarmak gerekiyor.

Temel fonksiyonların sürekliliği

Belirli fonksiyon türleri, özellikleri gereği süreklidir:

Sabit fonksiyonlar tüm reel sayılarda süreklidir.

$f(x)=k$

Polinom fonksiyonları tüm gerçek sayılar için süreklidir.

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Rasyonel (veya kesirli) fonksiyonlar, kesrin paydasını iptal eden değerler dışındaki tüm reel sayılarda süreklidir, bu noktalarda fonksiyon bir süreksizlik gösterir.

$f(x)=\cfrac{p(x)}{q(x)}$

Üstel fonksiyonlar tüm gerçek sayılar üzerinde süreklidir:

$f(x)=a^x$

Logaritmik fonksiyonlar argümanlarını pozitif kılan her noktada süreklidir.

$f(x)=\log_a (x)$

İrrasyonel fonksiyonların veya kökleri olan fonksiyonların sürekliliği, (n) radikalinin indeksine bağlıdır. İndeks çift ise, bunlar kök argümanını sıfıra eşit veya sıfırdan büyük yapan tüm noktalarda sürekli fonksiyonlardır. Ancak indeks tek ise, bunlar tüm reel sayılar üzerinde sürekli fonksiyonlardır.

$f(x)=\sqrt[n]{x}$

Trigonometrik fonksiyonların sürekliliği fonksiyonun türüne bağlıdır. Sinüs fonksiyonu ve kosinüs fonksiyonu gerçek sayılar kümesi üzerinde süreklidir, ancak teğet fonksiyonu noktalarda süreksizdir.
$\displaystyle x=\frac{\pi}{2}+k\pi$

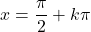
(burada k bir tamsayıdır).

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

Sürekli fonksiyonların özellikleri

Sean

$f(x)$

$g(x)$

noktada iki sürekli fonksiyon

$x=a,$

Bir noktadaki iki sürekli fonksiyonun toplamı, o noktadaki başka bir sürekli fonksiyondur.

$f(x)+g(x)$

Bir noktadaki iki sürekli fonksiyonun çarpımı, o noktadaki başka bir sürekli fonksiyona eşittir.

$f(x)\cdot g(x)$

İki sürekli fonksiyonun bir noktada bölünmesi, o nokta bölme fonksiyonunu iptal etmediği sürece, o noktada başka bir sürekli fonksiyonla sonuçlanır.

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

Bir noktada iki sürekli fonksiyonun bileşkesi aynı noktada sürekli bir fonksiyona yol açar.

$f(x)\circ g(x)$

➤ Bakınız: bileşik fonksiyon nedir?

Bir fonksiyonun sürekliliği ile ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki grafikte gösterilen fonksiyonun süreksizliklerini bulun. Ayrıca ne tür bir süreksizlik olduğunu da belirleyin.

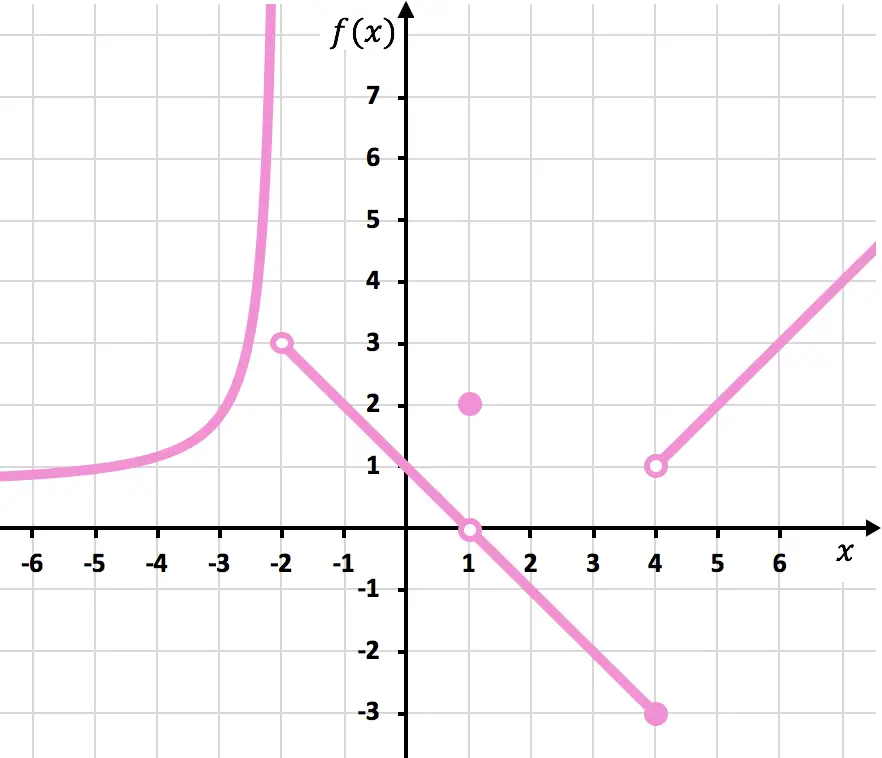
egzersiz fonksiyonlardaki süreksizlikleri çözdü

Not: Bu alıştırmayı gerçekleştirmek için öncelikle farklı süreksizlik türlerinin neler olduğunu ve nasıl tanımlandıklarını görmenizi öneririz. Açıklamayı süreksizlik türleri ilkesi bağlantısında görebilirsiniz.

Çözümü görün

Fonksiyonu çizmek için kalemi x=-2, x=1 ve x=4 noktalarına kaldırmalısınız. Dolayısıyla fonksiyon bu üç noktada süreksizdir.

x=-2’de sol taraftaki limit +∞ ve sağdaki limit 3’tür. Dolayısıyla, yan limitlerden biri sonsuz olduğundan fonksiyonun x=-2 noktasında kaçınılmaz bir sonsuz atlama süreksizliği vardır.

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

Fonksiyonun x=1 noktasındaki limiti 0’dır ve diğer taraftan fonksiyonun x=1 noktasındaki değeri 2’ye eşittir. Bu nedenle fonksiyon, x=1 noktasında kaçınılabilir bir süreksizlik sunar.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

x = 4’te sol taraftaki limit -3 ve sağ taraftaki limit 1’dir. Dolayısıyla iki kenar limiti farklı olduğundan ve ikisi de sonsuzluğu vermediğinden, fonksiyonun x =4 noktasında kaçınılmaz olarak sonlu atlama süreksizliği vardır.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Alıştırma 2

Aşağıdaki grafikte gösterilen fonksiyonun süreksiz olduğu noktaları belirleyiniz.

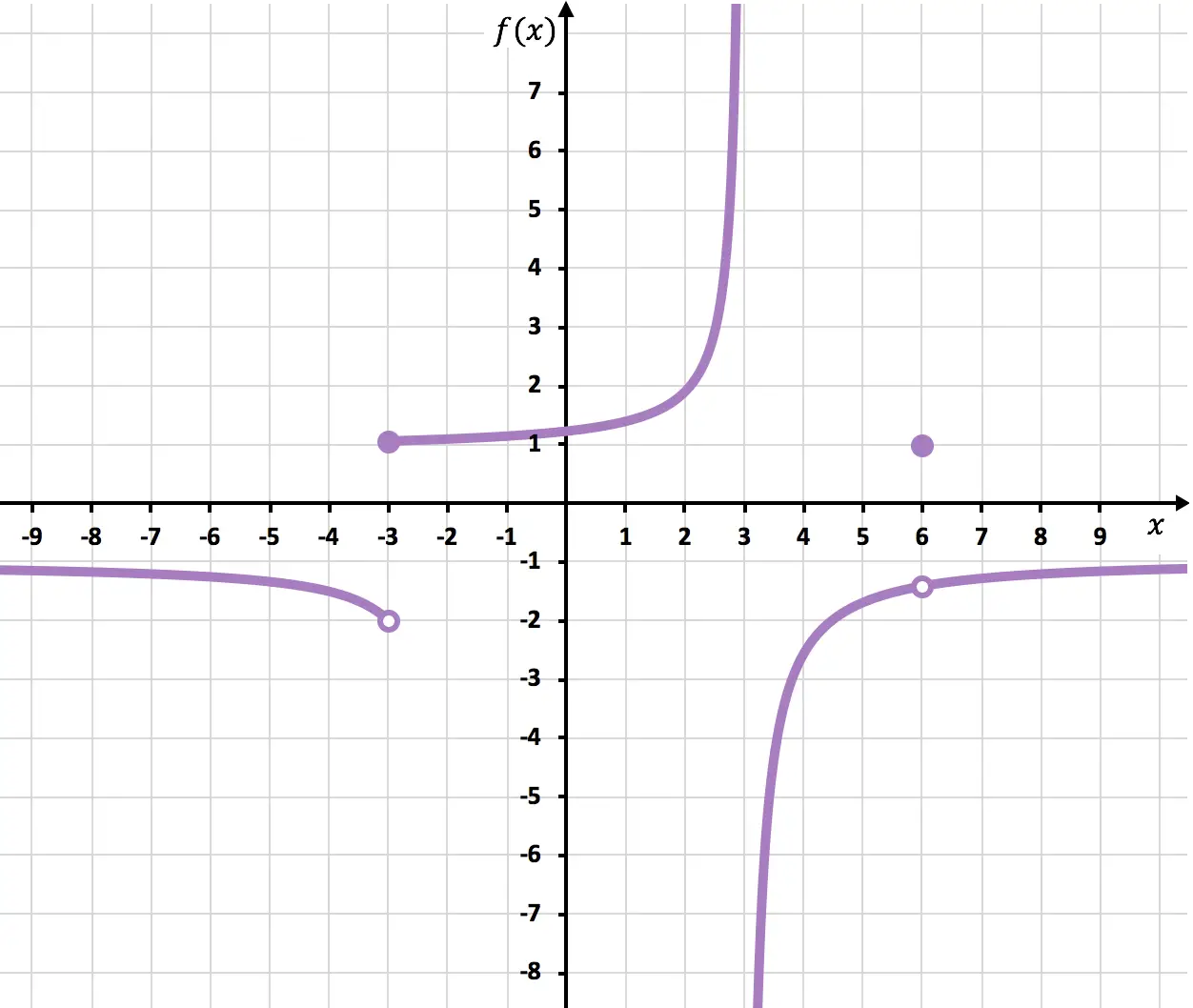
Bir fonksiyonun süreksizlik türleri üzerine çözülmüş alıştırma

Çözümü görün

x=6 noktasında açık bir nokta olduğundan fonksiyon kesintiye uğrar. X 6’ya yaklaşırken limit -1,4’tür ancak f(6)=1’dir. Dolayısıyla fonksiyon x=6’da önlenebilir bir süreksizliğe sahiptir çünkü limitin değeri fonksiyonun değeriyle çakışmaz:

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

x=-3’te yanal sınırlar çakışmaz ve hiçbiri sonsuzluğu vermez. Dolayısıyla fonksiyon x=-3’te kaçınılmaz bir sonlu atlama süreksizliğine sahiptir.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

Ve son olarak, bu noktada en az bir yanal limit sonsuzluğa yol açtığından, fonksiyonun x = 3’te kaçınılmaz bir sonsuz atlama süreksizliği vardır.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Alıştırma 3

Aşağıdaki rasyonel fonksiyonun sürekliliğini analiz edin:

$\displaystyle f(x)= \frac{2}{x-5}$

Çözümü görün

Rasyonel fonksiyonlar tüm etki alanlarında, yani paydayı iptal eden değerler dışındaki tüm reel sayılarda süreklidir. Bu nedenle hangi noktaların tanım kümesine ait olmadığını görmek için rasyonel fonksiyonun paydasını sıfıra eşitliyoruz:

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

Dolayısıyla fonksiyon x=5 dışındaki tüm noktalarda sürekli olacaktır.

Alıştırma 4

Aşağıdaki parçalı fonksiyonun sürekliliğini analiz edin:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

Çözümü görün

Fonksiyon ilk bölümde de süreklidir,

$5x-2$

ikinci bölümde olduğu gibi,

$x^2+2$

çünkü bunlar polinom fonksiyonlardır.

Dolayısıyla fonksiyonun süreksiz olabileceği tek nokta, fonksiyonun parçalı olarak kırıldığı noktadır. O halde bu noktada yanal sınırları hesaplayalım:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

Bu nedenle iki yanal limit çakışır, x 1’e yöneldiğinde fonksiyonun limiti 3’e eşittir:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

Ayrıca x=1’in görüntüsü de 3’tür:

$f(1)=1^2+2=\bm{3}$

Dolayısıyla fonksiyonun x=1 noktasındaki limiti söz konusu noktanın görüntüsüne eşit olduğundan fonksiyon x=1 noktasında süreklidir. Dolayısıyla tüm reel sayılarda süreklidir.

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

Alıştırma 5

Aşağıdaki irrasyonel fonksiyonun sürekliliğini inceleyin:

$f(x)=\sqrt{2x+6}$

Çözümü görün

Çift indeksli bir radikal fonksiyondur, dolayısıyla radikalin argümanı 0’dan büyük olduğu sürece fonksiyon sürekli olacaktır (çünkü negatif bir sayının karekökü mevcut değildir):

$2x+6\ge 0$

Eşitsizliği çözüyoruz:

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

Çözüm -3’ten büyük veya ona eşit olan tüm sayılardan oluşur. Bu nedenle fonksiyon, tanım kümesinin aralığında süreklidir:

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

Alıştırma 6

Aşağıdaki logaritmik fonksiyonun sürekliliğini analiz edin:

$f(x)=\log_3 (-3x+6)$

Çözümü görün

Bu logaritmik bir fonksiyondur ve ne negatif bir sayının logaritması ne de 0’ın logaritması vardır. Bu nedenle, logaritmanın argümanı pozitif (sıfırdan büyük) olduğu sürece fonksiyon mevcut olacaktır:

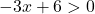$-3x+6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ Eşitsizliği çözüyoruz:

$-3x>-6″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”78″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{-6}{-3}$

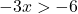
Negatif bir sayıyı bir eşitsizliğin diğer tarafına böldüğünüzde eşitsizliğin işaretini ters çevirmeniz gerektiğini unutmayın.

$x<2$

Çözüm, 2’den küçük tüm sayılardan oluşur. Dolayısıyla fonksiyonun tanım kümesi şu şekildedir:

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

Bu nedenle fonksiyon tanım kümesindeki her noktada süreklidir.

Egzersiz 7

Aşağıdaki fonksiyonun sürekliliğini hesaplayın:

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

Çözümü görün

Kesrin paydasında çift indeksli bir radikalimiz var, dolayısıyla fonksiyon kökün içeriği sıfıra eşit veya sıfırdan büyük olduğunda mevcut olacaktır:

$-2x-8\geq 0$

Ancak aynı zamanda kök, kesrin paydasındadır ve bir kesrin paydası hiçbir zaman 0 olamaz. Dolayısıyla fonksiyon yalnızca kökün içeriği 0’dan büyük olduğunda var olacaktır:

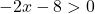$-2x-8> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ Şimdi eşitsizliği çözüyoruz:

$-2x>8″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”64″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{8}{-2}$

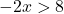
Negatif bir sayının kenarlarını bir eşitsizliği çarparak veya bölerek değiştirdiğimizde eşitsizlik işaretini de döndürmemiz gerektiğini unutmayın.

$x<-4$

Sonuç -4’ten küçük tüm sayılardır. Böylece fonksiyonun tanım kümesi ve dolayısıyla sürekliliği aşağıdaki aralıkla tanımlanır:

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

Egzersiz 8

Fonksiyonun baştan sona sürekli olmasını sağlayacak şekilde k değerini hesaplayın.

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”> <div class=$

Çözümü görün

Fonksiyonun sürekli olabilmesi için kırılma noktasındaki iki yanal limitin aynı sonucu vermesi gerekir. Bu nedenle öncelikle k içermeyen parçanın kırılma noktasındaki yanal limiti hesaplıyoruz:

$\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}$

Dolayısıyla parçalı fonksiyonun sürekli olabilmesi için diğer kenar limitinin de 7’ye eşit olması gerekir.

$\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1$

Dolayısıyla fonksiyonun sürekli olabilmesi için herhangi bir noktanın iki yanal limitinin aynı sonucu vermesi gerekir. Bu nedenle limitten elde edilen ifadeyi 7’ye (diğer yanal limitin sonucu) eşitliyoruz.