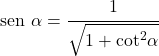Bu sayfada sinüs fonksiyonu hakkında her şeyi bulacaksınız: nedir, formülü nedir, grafikte nasıl gösterilir, bu tür fonksiyonun özellikleri, genlik, periyot vb. Ek olarak, kavramı tam olarak anlamak için sinüs fonksiyonlarının farklı örneklerini görebileceksiniz. Hatta sinüs teoremini ve sinüs fonksiyonunun diğer trigonometrik oranlarla olan ilişkilerini bile açıklıyor.
sinüs fonksiyonu formülü
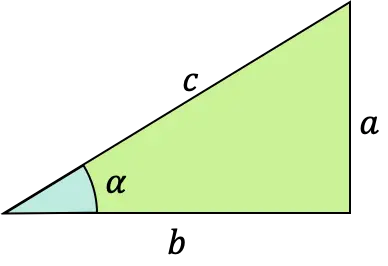
Bir α açısının sinüs fonksiyonu , formülü bir dik üçgenin (dik açılı üçgen) karşı kenarı ile hipotenüsü arasındaki oran olarak tanımlanan trigonometrik bir fonksiyondur.

Bu tür matematiksel fonksiyon genellikle “sin” veya “sin” (Latince sinüsten ) kısaltmasıyla yazılır. Ek olarak sinüzoidal, sinüzoidal veya sinüzoidal fonksiyon olarak da adlandırılabilir.
Sinüs fonksiyonu, bir açının kosinüsü ve tanjantıyla birlikte en iyi bilinen trigonometrik oranlardan biridir.
Sinüs fonksiyonunun karakteristik değerleri
Bazı açılar sıklıkla tekrarlanır ve bu nedenle sinüs fonksiyonunun değerini bu açılarda bilmek uygundur:
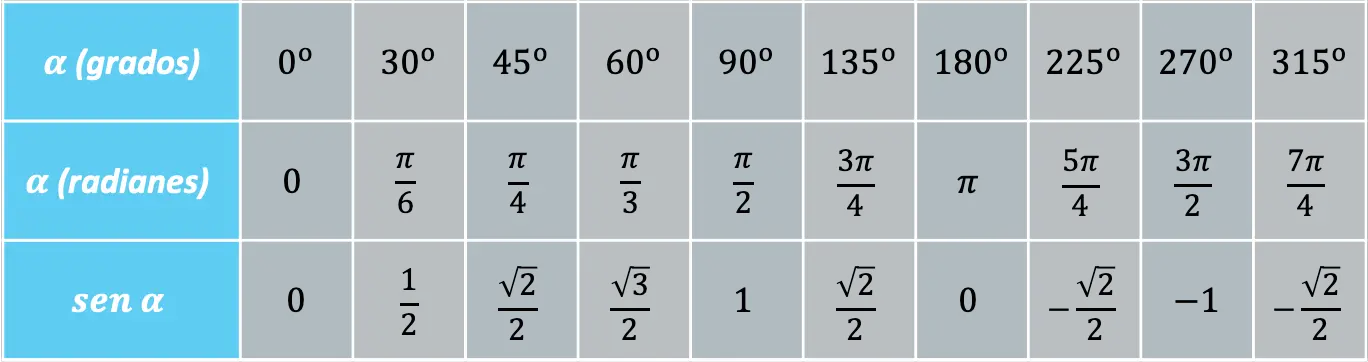
Dolayısıyla sinüs fonksiyonunun işareti, açının bulunduğu çeyreğe bağlıdır: eğer açı birinci veya ikinci çeyrekte ise sinüs pozitif olacaktır, diğer yandan açı üçüncü veya dördüncü çeyrekte ise sinüs pozitif olacaktır. sinüs negatif olacaktır.
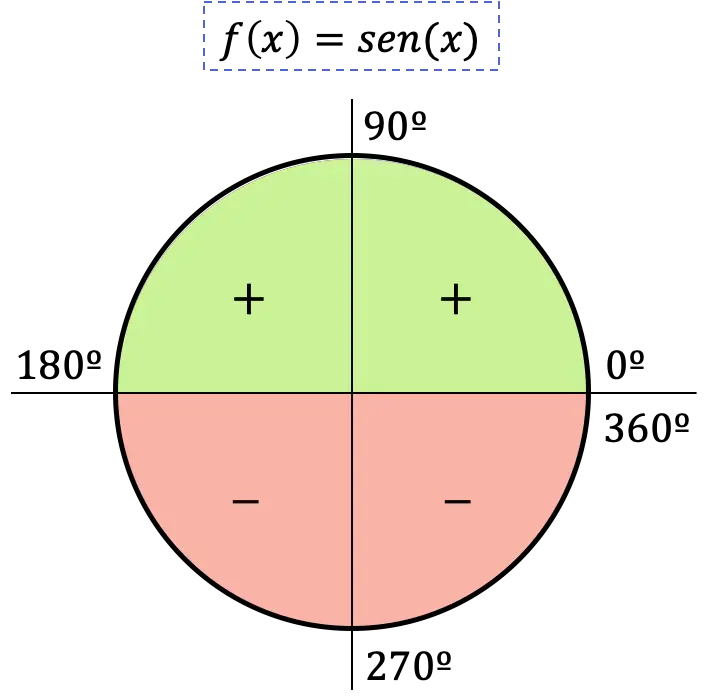
Sinüs fonksiyonunun grafiksel gösterimi
Önceki bölümde gördüğümüz değerler tablosu ile sinüs fonksiyonunun grafiğini çizebiliriz. Yani sinüs fonksiyonunun grafiğini çizdiğimizde şunu elde ederiz:
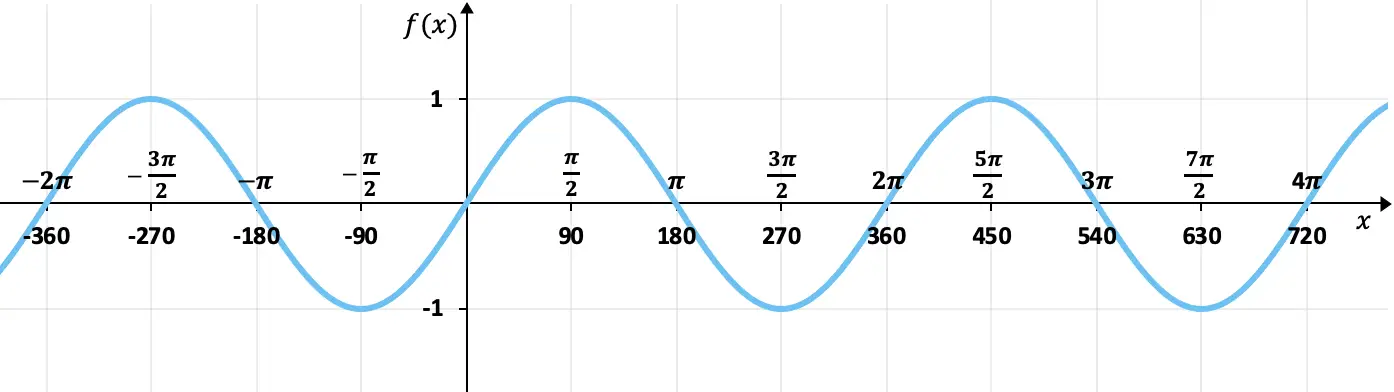
Grafikten de görebileceğiniz gibi sinüs fonksiyonunun görüntülerinin değerleri her zaman +1 ile -1 arasındadır, yani üstte +1, altta -1 ile sınırlanmıştır. Ayrıca değerler her 360 derecede (2π radyan) tekrarlanır, dolayısıyla periyodu 360° olan periyodik bir fonksiyondur .
Öte yandan, bu grafikte sinüs fonksiyonunun tek olduğunu çok iyi anlıyoruz, çünkü karşıt elemanları zıt görüntülere sahip, yani orijine (0,0) göre simetrik. Örneğin 90°’nin sinüsü 1, -90°’nin sinüsü -1’dir.
Sinüs fonksiyonunun özellikleri
Sinüs fonksiyonu aşağıdaki özelliklere sahiptir:
- Sinüs fonksiyonunun alanının tamamı gerçek sayılardır, çünkü grafiğin gösterdiği gibi, fonksiyon bağımsız değişken x’in herhangi bir değeri için mevcuttur.
![]()
- Sinüs fonksiyonunun yolu veya aralığı eksi 1’den artı 1’e kadardır (her ikisi de dahil).
![]()
- Periyodikliği 2π olan sürekli ve tek bir fonksiyondur.
![]()
- Bu tip trigonometrik fonksiyonun y ekseni (Y ekseni) ile (0,0) noktasında tek bir kesişme noktası vardır.
![]()
- Bunun yerine periyodik olarak apsisi (X ekseni) pi’nin çeşitli koordinatlarında keser.
![]()
- Sinüs fonksiyonunun maksimumu şu durumlarda ortaya çıkar:
![]()
- Ve tersine, sinüs fonksiyonunun minimumu şu noktada gerçekleşir:
![]()
- Sinüs fonksiyonunun türevi kosinüstür:
![]()
- Son olarak sinüs fonksiyonunun integrali, kosinüs değiştirilmiş işaretidir:
![]()
Sinüs fonksiyonunun periyodu ve genliği
Grafiğinde gördüğümüz gibi sinüs fonksiyonu periyodik bir fonksiyondur yani değerleri bir frekansa göre tekrarlanır. Ek olarak salınım yaptığı maksimum ve minimum değerler genliğine bağlıdır. Bu nedenle sinüzoidal fonksiyonu belirleyen iki özellik periyodu ve genliğidir:
![]()
- Sinüs fonksiyonunun periyodu, grafiğin tekrarlandığı iki nokta arasındaki mesafedir ve aşağıdaki formülle hesaplanır:
![]()
- Sinüs fonksiyonunun genliği sinüs teriminin önündeki katsayıya eşdeğerdir.
![]()
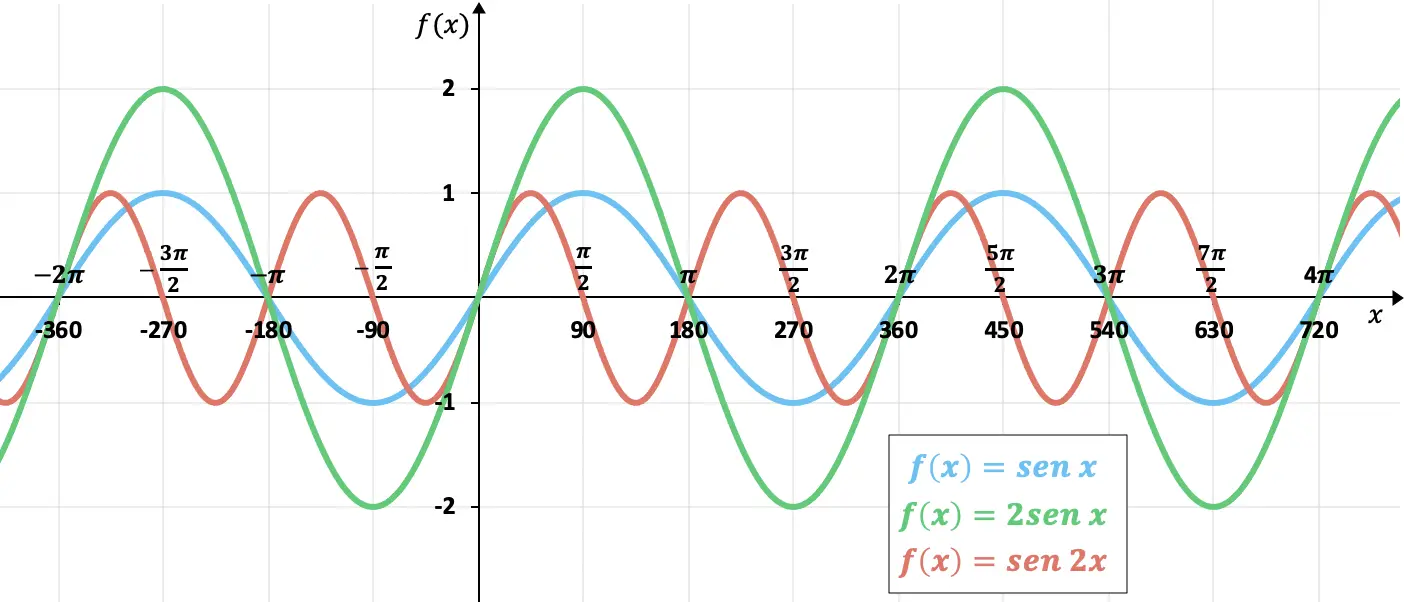
Aşağıda periyodu veya genliği değiştirmenin etkilerini gösteren bir grafik görebilirsiniz:

Yeşil renkle gösterilen fonksiyonda, genliğin iki katına çıkarılmasıyla fonksiyonun +1’den -1’e değil, +2’den -2’ye gittiğini görebiliriz. Öte yandan kırmızıyla gösterilen fonksiyonda periyodu yarıya indirildiği için “kanonik” sinüs fonksiyonundan iki kat daha hızlı gittiğini görebilirsiniz.
sinüs teoremi
Sinüs normalde dik üçgenlere uygulansa da, her tür üçgen için işe yarayan bir teorem de vardır: sinüs(ler) teoremi.
Sinüs kanunu herhangi bir üçgenin kenarlarını ve açılarını şu şekilde ilişkilendirir:
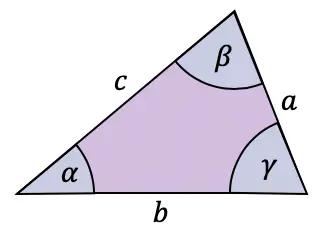
![]()
Sinüs fonksiyonunun diğer trigonometrik oranlarla ilişkileri
Aşağıda trigonometrideki en önemli trigonometrik oranlarla sinüzoidal ilişkileri bulacaksınız.
Kosinüs oranı
- Kosinüs fonksiyonunun grafiği sinüs eğrisine eşdeğerdir ancak kaydırılmıştır
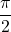
sola doğru, böylece iki işlev aşağıdaki ifadeyle ilişkilendirilebilir:
![]()
- Ayrıca sinüs ve kosinüsü trigonometrik temel özdeşlikle ilişkilendirebilirsiniz:
![]()
teğet ile ilişki
- Kanıtlanması karmaşık olmasına rağmen sinüs yalnızca teğete göre ifade edilebilir:
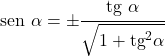
Kosekant ile ilişki
- Sinüs ve kosekant çarpımsal terslerdir:
![]()
Sekant ile ilişki
- Sinüs, yalnızca sekant değerine bağlı olacak şekilde silinebilir:
![]()
Kotanjant ile ilişki
- Bir açının sinüsü ve kotanjantı aşağıdaki denklemle ilişkilidir: