Sabit fonksiyon - Mathority

Bu yazıda sabit fonksiyonun ne olduğunu ve grafiksel gösteriminin ne olduğunu açıklıyoruz. Ek olarak, sabit fonksiyonların çeşitli örneklerini ve bu tip fonksiyonların tüm özelliklerini görebileceksiniz. Ve son olarak, sabit fonksiyonların çözülmüş alıştırmalarıyla antrenman yapabileceksiniz.

Sabit fonksiyon nedir?

Sabit bir fonksiyon, bağımsız değişken (x)’in herhangi bir değeri için her zaman aynı görüntüyü alan fonksiyondur ; yani sabit bir fonksiyon f(x)=k biçimindedir, burada k herhangi bir gerçek sayıdır.

$f(x)=k$

Sabit bir fonksiyonun grafiksel gösterimi yatay bir çizgidir.

Örneğin, aşağıdaki işlevlerin tümü sabittir:

$f(x)=1 \qquad f(x)=7 \qquad f(x)=5$

Sabit bir fonksiyonun grafiksel gösterimi

Sabit fonksiyon kavramını gördükten sonra, sabit bir fonksiyonun grafikte nasıl temsil edileceğini göreceğiz.

Sabit bir fonksiyonun grafiğini çizmek oldukça basittir; fonksiyonun (k) değerine yatay bir çizgi çizmeniz yeterlidir.

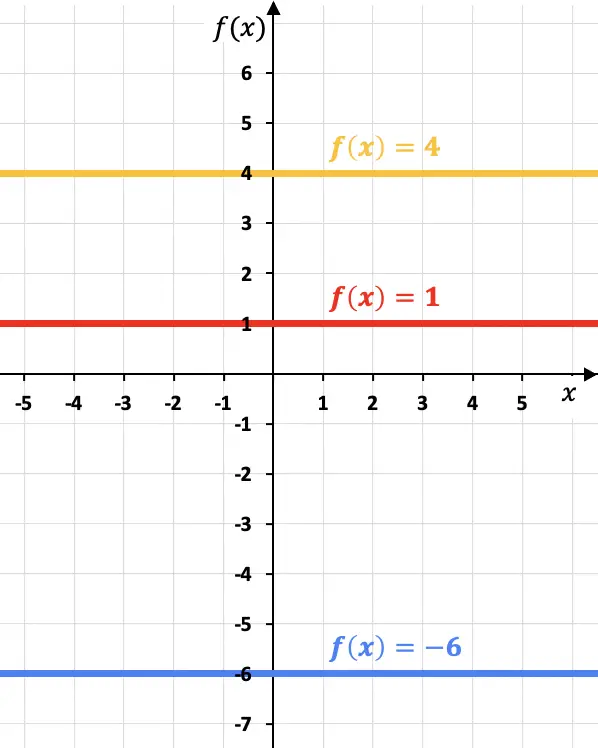
Üç farklı sabit fonksiyonu grafik üzerinde temsil ettiğimiz aşağıdaki örneklere bakın:

Her sabit fonksiyonun x eksenine paralel olduğuna dikkat edin.

Öte yandan dikey bir doğrunun sabit bir fonksiyon olmadığını da unutmamalısınız. Aslında dikey bir çizgi bir fonksiyon bile değildir, çünkü tanım gereği bir fonksiyon her x değeri için yalnızca bir görüntüye sahip olabilir.

Sabit fonksiyonun özellikleri

Daha sonra sabit fonksiyonun özelliklerini analiz edeceğiz. Herhangi bir değerin sabit bir fonksiyonunu düşünün:

$f(x)=k$

Sabit fonksiyonun tanım kümesinin tümü gerçek sayılardır:

$\text{Dom } f = \mathbb{R}$

Sabit fonksiyonun yolu veya aralığı yalnızca sabitin değeridir:

$\text{Im } f= k$

Sürekli ve eşit bir fonksiyondur çünkü fonksiyon her zaman aynı değeri alır:

$\displaystyle f(x)=f(-x)$

Sabit fonksiyon ne artan ne de azalan bir fonksiyondur, eğimi her zaman sıfır olan bir fonksiyon türüdür:

$m=0$

OY eksenini her zaman (0,k) noktasında keser.

$(0,k)$

Her sabit fonksiyon sıfır dereceli bir polinomdur.

Evet
$k\neq 0$

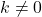
sabit fonksiyonun kökü yoktur, bunun yerine, eğer

$k=0$

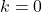
tüm gerçek sayılar sabit fonksiyonun kökleridir.

x artı sonsuza veya eksi sonsuza yaklaşırken sabit fonksiyonun limiti, sabitin değerine eşittir:

$\displaystyle\lim_{x\to +\infty} f(x)=k$

$\displaystyle\lim_{x\to -\infty} f(x)=k$

Sabit fonksiyonun türevi her zaman sıfırdır:

$f(x)=k \ \longrightarrow \ f'(x)=0$

Aslında sabit fonksiyonun tanımı türev kavramından da yapılabilir: Bir fonksiyon, eğer türevi tüm tanım kümesinde sıfırsa sabittir.

Sabit fonksiyonun integrali doğrusal (veya afin) fonksiyondur:

$\displaystyle \int k \ dx= x + C$

➤ Bakınız: Doğrusal fonksiyon nedir?

Bir aralıkta sabit fonksiyon

Bir fonksiyonun nasıl sabit olduğunu gördük, ancak bir fonksiyon ancak tanım kümesinin bir aralığında sabit olabilir.

Bu kavramı anlamak için hangi işlevlerin parçalar halinde tanımlandığını bilmeniz gerekir; bu nedenle devam etmeden önce aşağıdaki açıklamaya göz atmanızı öneririz:

➤ Bakınız: Parçalı fonksiyon nedir?

Bu tür fonksiyonların ne olduğunu öğrendikten sonra aşağıda gösterilen bölümlerde tanımlanan fonksiyona bakın:

Grafikten görebileceğiniz gibi fonksiyon tanım kümesindeki tüm sayılar için sabit değildir. Ancak [-2,4 aralığında sabittir), dolayısıyla yalnızca bir aralıkta sabit bir fonksiyondur.