Rasyonel sayıların diğer sayılardan ne kadar farklı olduğunu hiç merak ettiniz mi? Bu yazıda rasyonel sayıları, benzersiz özellikleri ve sınıflandırılması da dahil olmak üzere derinlemesine inceleyeceğiz. Konsepti daha iyi anlamaya hazır olun!
Rasyonel sayılar nedir?
Rasyonel sayılar (ℚ), kesir olarak ifade edilebilen tüm sayıları içeren gerçek sayıların bir alt sınıfıdır. Bu, rasyonel sayıların, b ≠ 0 olmak üzere iki tam sayının a/b oranı olarak yazılabilen sayılar olduğu anlamına gelir.
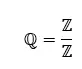
Rasyonel sayılar tekrarlanan rakamlardan oluştuğu için tekrarlanan veya sonlu ondalık sayılar olarak da ifade edilebilir. Rasyonel sayıların bazı örnekleri 1/2, 3/4, 10/3, 2/3 ve π (pi)’dir.
Rasyonel alt kümeler
Rasyonel sayılar iki alt gruba ayrılabilir:
- 0’ı, tüm doğal sayıları ve tüm negatif sayıları içeren tamsayılar .
- Ondalık sayılar veya kesirli sayılar , bunların tümü aşağıdakilerden oluşan değerleri ifade eder: bir tamsayı kısmı ve bir ondalık kısım; ikincisi birlikten daha küçük değerlerin ifade edilmesine izin verir.

Gerçek sayılar kümesinin bir diğer alt kategorisi ise biraz daha karmaşık olan irrasyonel sayılardır .
Rasyonel Sayılara Örnekler
Rasyonel sayılar kesir olarak, yani iki tam sayının bölümü olarak ifade edilebilen sayılardır. Rasyonel sayılara bazı örnekler:
-23
-4/5
-1/2
-7/9
Bir tam sayıyı temsil eden tüm kesirler eşit derecede rasyoneldir. Örneğin:
-1/1
-2/2
-3/3
Rasyonel sayıların özellikleri
Rasyonel sayıların temel özelliği, paydalarının her zaman sıfırdan farklı olmasıdır.
Bu kümenin ikinci özelliği, her rasyonel sayının sonsuz sayıda eşdeğer kesirle temsil edilebilmesidir. Örneğin 7/2’ye eşit olan 3,5 rasyonel sayısı aynı zamanda 14/4, 28/8… ve diğer kesirlerden oluşan sonsuz sayıda da yazılabilir.
Rasyonel sayılar aynı zamanda dağılma özelliğini de karşılar. Bu, bir kesri diğeriyle çarpmanın veya bölmenin sonucu etkilemeyeceği anlamına gelir:
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (reklam)/(bc)
Rasyonel sayıların gösterimi
Rasyonel sayılar çeşitli şekillerde temsil edilebilir, ancak en yaygın olanı kesirli olanıdır . Bir kesir iki sayıdan oluşur: pay ve payda.
Pay, bütünün kaç parçasının dikkate alındığını, payda ise bütünün kaç eşit parçasının olduğunu gösterir. Örneğin bir pastayı sekiz eşit dilime bölüp bu dilimlerden üçünü yersek, yenen kek miktarını ifade eden kesir 3/8 olur.
Rasyonel sayıları temsil etmenin bir başka yolu da ondalık sayılardır. Ondalık sayılar, paydası 10, 100, 1000 vb. bir sayı olan kesirleri yazmanın kısa yoludur. Örneğin, bir pastanın 1/4’üne sahipseniz, bu 0,25 (“0 tam ve 25/100” anlamına gelir) olarak ifade edilebilir.
Ancak grafiksel olarak göstermek istersek sayıların sırasının çok iyi görülebildiği sayı doğrusuna da yazabiliriz. Daha sonra size bu satırın bir örneğini gösteriyoruz:
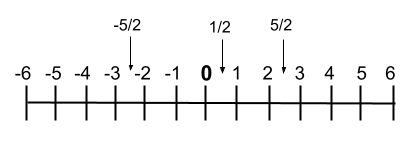
rasyonel işlemler
Rasyonel sayıların temel işlemleri tam sayılarla aynıdır: toplama, çıkarma, çarpma ve bölme. Bu tür işlemlerin nasıl çözüleceğini öğrenmek istiyorsanız kesirlerle işlemler hakkındaki yazımızı okumanızı öneririz.
Ancak ondalık tabana sahip rasyonel sayılarla çalışıyorsanız, ondalık değerlerle uğraşırken kullandığınız işlemleri çözme prosedürünü izlemelisiniz.
Rasyonel sayılar kümesine ilişkin sonuç
Bu kapsamlı açıklamadan sonra rasyonel sayılar kümesinin matematikteki en önemli kümelerden biri olduğu sonucuna varabiliriz. Kesir olarak gösterilebilecek tüm sayıları içerir, bu da miktarları çok hassas bir şekilde ifade etmemizi sağlar.