Bir kökten türetilmiştir

Burada bir kökün (veya bir radikal fonksiyonun) türevinin nasıl alınacağını açıklıyoruz. Kökleri bölme formülünü bulacaksınız ve köklerin türevleri için adım adım çözülmüş alıştırmalar bulacaksınız.

Bir kökün türevinin formülü

Bir kökün türevi veya irrasyonel fonksiyon, kökün türevinin (kökün altındaki ifade), kökün indeksinin çarpımına aynı kökün çarpımına bölünmesine ve kökün üssünden 1 çıkarılmasına eşittir.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Ancak kök kök yalnızca bir x ise formüller basitleşir. Dolayısıyla x’in kök türevi aşağıdaki gibidir:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Kısacası, kök türetmenin iki formülü vardır: Birincisi her zaman kullanılabilecek, ikincisi ise yalnızca kök x olduğunda kullanılabilecek.

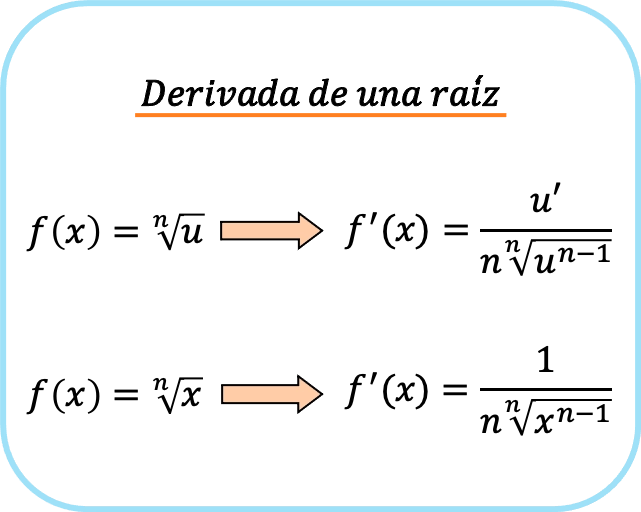
Yakından bakıldığında kesrin payındaki terimin, kökün türevi alınırken zincir kuralının uygulanmasından kaynaklanan terim olduğu görülür. Bu nedenle kök x olduğunda, x’in türevi olduğundan paydada 1 görünür.

Kök türevleri örnekleri

Bir radikal fonksiyonun türevinin formülü göz önüne alındığında, bir kökün türevinin nasıl alınacağını anlamanız için aşağıda bu türevin birkaç örneğini açıklıyoruz.

Örnek 1: Karekökün türevi

Daha sonra karekökün türevinin ne olduğunu göreceğiz:

$f(x)=\sqrt{x}$

Bu durumda kökün içindeki ifade yalnızca bir x olduğundan aşağıdaki formülü kullanabiliriz:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Yani bir karekökün türevi, 1 bölü x’in karekökünün 2 çarpımına eşittir:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Örnek 2: Küp kökünün türevi

$f(x)=\sqrt[3]{x}$

Bu örnekte kökün altındaki ifade bir x olduğundan aşağıdaki formülü uygulayabiliriz:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Yani bir küp kökünün türevi eşittir 1 bölü 3 çarpı küp kök x kare:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Örnek 3: Dördüncü kökün türevi

$f(x)=\sqrt[4]{7x-2}$

Şimdi radikal işaretinin altında bir x yok ama daha karmaşık bir cebirsel ifademiz var. Bu nedenle bir kökün türevi için genel formülü kullanmalıyız:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Radikalin altındaki ifade birinci dereceden bir fonksiyon olduğundan türevi 7’dir. Dolayısıyla tüm fonksiyonun türevi:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Örnek 4: Bir kökten diğerine türetme

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Bu kökün başka bir kökten oluşan türevini çözmek için aşağıdaki formülü uygulamamız gerekir:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Bu durumda türevi hesaplamak için aynı formülü arka arkaya iki kez kullanmanız gerekir:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Bir kökün türeviyle ilgili çözülmüş problemler

Aşağıdaki köklerin türevlerini hesaplayın:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

çözümü gör

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Bir kökün türevinin formülü

Kök türevleri örnekleri

Örnek 1: Karekökün türevi

Örnek 2: Küp kökünün türevi

Örnek 3: Dördüncü kökün türevi

Örnek 4: Bir kökten diğerine türetme

Bir kökün türeviyle ilgili çözülmüş problemler

Yorum bırakın Yanıtı iptal et