Polinomları toplama

Bu sayfada polinomların toplanmasının nasıl yapıldığına dair açıklama bulacaksınız. Ek olarak, polinom toplamlarının örneklerini ve hatta adım adım çözülen alıştırmaları görebileceksiniz. Son olarak polinomlarla yapılan bu tür işlemlerin özelliklerinin neler olduğunu da açıklıyoruz.

Polinomlar nasıl eklenir?

Matematikte iki veya daha fazla polinomun toplanması için polinomların benzer terimlerinin toplanması gerekir. Yani polinomların eklenmesi, aynı değişmez kısma sahip (aynı değişkenler ve aynı üsler) terimlerin eklenmesinden oluşur.

Böylece polinomların toplamı iki farklı şekilde yapılabilir: dikey yöntemle veya yatay yöntemle. Aşağıda her iki prosedürün açıklaması bulunmaktadır, ancak önce polinomları dikey olarak nasıl toplayacağınızı öğrenmenizi ve ardından yatay yönteme geçmenizi öneririz. Açıkçası tercih ettiğinize sadık kalın.

Dikey polinomların eklenmesi

Daha sonra bir örnek kullanarak iki polinomun dikey olarak nasıl toplandığını göreceğiz:

Aşağıdaki iki polinomu ekleyin:

$P(x) = 6x^4+4x^3+2x-3$

$Q(x) = 3x^4-7x^3+6x^2-4x+1$

Yapmamız gereken ilk şey, iki polinomun benzer terimlerinin sütunlarla hizalanması için bir polinomu diğerinin altına yerleştirmektir:

Uyarı: Bir polinomun belirli derecede bir terimi yoksa boşluk bırakılmalıdır. Örneğin

$P(x)=6x^4+4x^3+2x-3$

Derece 2 monomialiniz yok, bu yüzden sitenizde boş bir alan var.

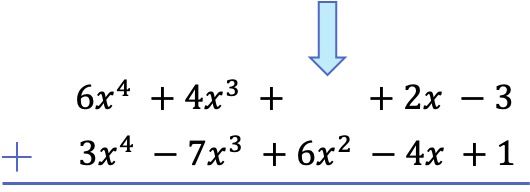
Tüm terimleri en yüksek dereceden en düşük dereceye kadar sıraladıktan sonra, her sütundaki katsayıları, gerçek kısımları eşit tutarak topluyoruz:

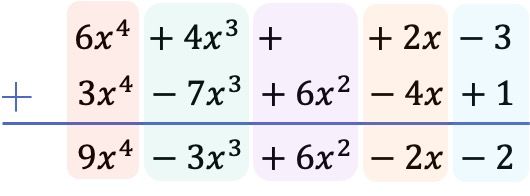
Sonuç olarak, 2 polinomun toplamından elde edilen sonuç:

$\bm{P(x)+Q(x) = 9x^4-3x^3+6x^2-2x-2}$

Artık polinomların toplamasını anladığınıza göre, polinomlardan oluşan kesirleri de toplayabileceğinizi bilin. Bu tür işlemlere cebirsel kesir toplama denir. Bu bağlantıya tıklayın ve sadece cebirsel kesirlerin toplamlarının nasıl hesaplandığını değil aynı zamanda cebirsel kesirlerle yapılan tüm işlemlerin nasıl çözüldüğünü de öğrenin.

Polinomların yatay eklenmesi

Az önce polinomların dikey olarak nasıl ekleneceğini gördük, ancak şimdi polinomları toplamanın diğer yöntemine bakacağız: polinomları yatay olarak eklemek. Elbette bu işlem öncekinden daha hızlıdır ancak polinom kavramlarına daha fazla hakim olmak gerekir.

Şimdi bu polinom toplama yönteminin nelerden oluştuğunu bir örnekle görelim. İki yöntem arasındaki farkları görebilmeniz için önceki örnekte olduğu gibi aynı polinomları ekleyeceğiz:

Aşağıdaki iki polinomun toplamını hesaplayın:

$P(x) = 6x^4+4x^3+2x-3$

$Q(x) = 3x^4-7x^3+6x^2-4x+1$

İlk önce iki polinomu aynı işlemde, yani birbiri ardına konumlandırmanız gerekir:

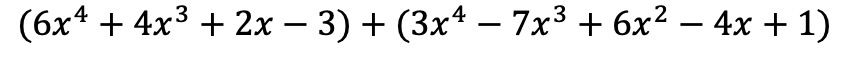
Ve şimdi aynı değişmez parçalara sahip terimleri, yani aynı değişkenlere (harflere) ve aynı üslere sahip terimleri ekliyoruz. Benzer olmayan terimler eklenemez.

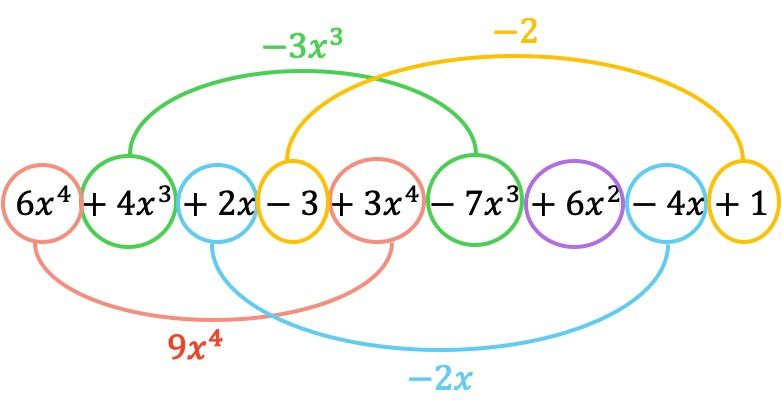
Toplamanın sonucunda ortaya çıkan polinom şu şekildedir:

Gördüğünüz gibi her iki yöntemle de aynı sonucu elde ettik, yani polinomları eklerken size en uygun olanı kullanabilirsiniz.

Polinomların eklenmesiyle ilgili çözülmüş problemler

Pratik yapabilmeniz için sizi polinomların toplamlarıyla ilgili birkaç çözülmüş alıştırmayla baş başa bırakıyoruz. Aklınıza takılan sorular varsa sayfadaki yorumlardan sorabilirsiniz, en kısa sürede cevaplayacağız.

1. Egzersiz

Aşağıdaki iki polinomu ekleyin:

$P(x) = 3x^3-5x^2+4x+1$

$Q(x) = 4x^3+x^2-9x+3$

Çözüme bakın

Bu durumda iki polinomu dikey olarak toplayacağız. Bunu yapmak için polinomları dereceye göre sıralıyoruz ve aynı sütunda bulunan monomları topluyoruz:

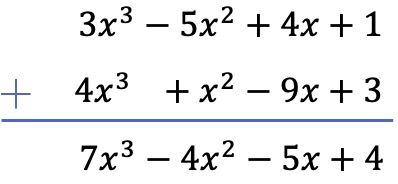
polinom toplamları ile ilgili çözülmüş alıştırmalar

Alıştırma 2

Aşağıdaki iki polinomun toplamını çözün:

$P(x) = 8x^4+2x^3+9x^2-3x-7$

$Q(x) = 5x^4+6x^3-4x+2$

Çözüme bakın

İki polinomu dikey yöntemi kullanarak toplayacağız. Bu nedenle polinomları dereceye göre sıralıyoruz ve aynı sütunda bulunan terimleri topluyoruz:

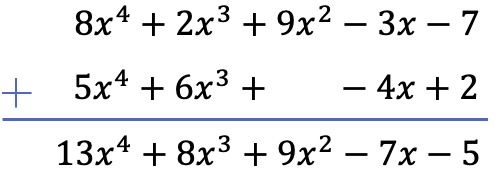
Bu özel durumda, ikinci polinomun ikinci derece sütununda bir boşluk bırakılması gerektiğine dikkat edin, çünkü ikinci dereceden bir terimi yoktur.

Alıştırma 3

Aşağıdaki iki polinomun toplamı nedir?

$P(x) = -3x^5+4x^4-2x^3-6x^2+2x-4$

$Q(x) = 6x^5-7x^4+8x^3-3x^2-6x+5$

Çözüme bakın

İki polinomun toplamasını dikey yöntemi kullanarak gerçekleştireceğiz. BU YÜZDEN:

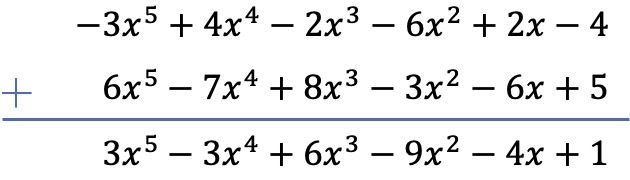
egzersiz polinomların toplamlarını adım adım çözdü

Alıştırma 4

Aşağıdaki üç polinomun toplamını hesaplayın:

$P(x) =6x^4-3x^3+8x^2+4x+5$

$Q(x) =-9x^4+5x^3+6x^2-2x+7$

$R(x) =-4x^4+6x^3-9x^2+6x-3$

Çözüme bakın

Dikey yöntemi kullanarak 3 polinomun toplamını hesaplayacağız. Bu nedenle polinomları dereceye göre sıralıyoruz ve aynı sütunda bulunan terimleri topluyoruz:

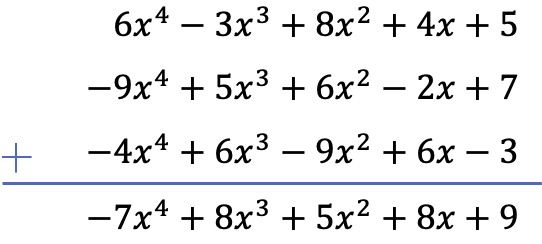
👉👉👉Artık iki polinomun nasıl toplandığını gördüğünüze göre, polinomların başka bir karakteristik işlemiyle ilgilenebilirsiniz: ortak çarpan. Bir polinomdan ortak bir çarpan çıkarmak oldukça karmaşıktır (ve anlaşılması zordur), aslında bunu yaparken birçok hata yapılır. Bu nedenle , ortak faktörün nasıl çıkarılacağını adım adım açıkladığımız bir rehber hazırladık, böylece bunu mükemmel bir şekilde anlayabilir ve bu işlemi yaparken hata yapmazsınız. Bağlantıya tıklayarak bir polinomdan ortak çarpanı çıkarmaya yönelik ipuçlarının neler olduğunu öğrenin.