▷ Polinomlar nasıl çarpılır (çözülmüş alıştırmalar)

Bu sayfada polinomların nasıl çarpıldığını öğreneceksiniz. Ayrıca polinomların çarpımına ilişkin örnekleri ve ayrıca adım adım çözülen alıştırmaları da görebileceksiniz. Son olarak çarpma polinomlarının özelliklerinin neler olduğunu keşfedeceksiniz.

Ancak polinomlarla çarpma kavramını tam olarak anlamak için en temelden en karmaşık olana doğru ilerleyeceğiz, yani bir polinomun bir sayıyla nasıl çarpılacağıyla başlayacağız ve sonra bir polinomun şu şekilde nasıl çarpılacağını göreceğiz: bir tek terimli ve son olarak iki veya daha fazla polinomun birlikte nasıl çarpılacağını açıklayacağız.

Bu sırayı takip etmenizi öneririm ancak önceki polinomlarla işlemlerde zaten ustalaştığınızı düşünüyorsanız indekse tıklayarak doğrudan polinomlar arası çarpma işlemine geçebilirsiniz:

Bir polinomu bir sayıyla çarpma

Bir skalerin (veya bir sayının) ve bir polinomun çarpımını çözmek oldukça basittir; sayıyı polinomun her teriminin katsayısıyla çarpmanız yeterlidir.

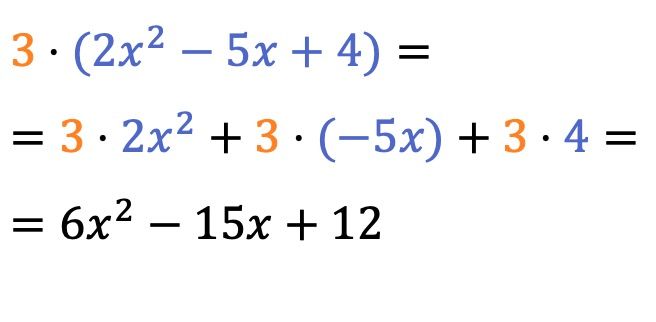
Parantezlerin önündeki çarpım işareti çıkartılabilir.

$\begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}$

Bir polinomun bir tek terimle çarpılması

Bir polinomun bir monomla nasıl çarpıldığını görmeden önce, monomların birbirleriyle nasıl çarpıldığını hatırlayacağız çünkü bu tür polinom işlemlerini yapabilmek için bunu bilmeniz gerekir.

İki monomiyelin çarpımı, katsayılarının birbirleriyle ve gerçek kısımlarının birbirleriyle çarpılmasından oluşur, yani monomların katsayıları çarpılır ve aynı tabana sahip değişkenlerin üsleri toplanır. Aşağıdaki örneğe bakın:

$3x^2 \cdot 4x^5 = (3\cdot 4) x^{2+5} = 12x^7$

Şimdi bir tek terimliyi bir polinomla nasıl çarpacağımızı görelim:

Matematikte, bir tek terimlinin bir polinomla çarpımını çözmek için, tek terimli polinomdaki her terimle çarpılır.

bir polinomun bir monomiyal ile çarpılması

Daha önce olduğu gibi çarpma işareti de atlanabilir:

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

Önceki örnekte, tek terimlileri veya polinomları çarparken işaret kuralını da dikkate almanız gerektiğine dikkat edin. Aslında, tek terimlileri ve polinomları çarparken çok yaygın bir hata, bir terimin işaretini yanlış almaktır.

Elbette bir noktada matematikte yeni bir şey gördüğünüzde kendinize şu soruyu sordunuz: Bu ne için ? Bu tür çarpma, bir polinomun ortak faktörünü elde etmek için kullanılır; bu, polinomları basitleştirmenize olanak tanıyan bir işlemdir (çok faydalıdır). Bunun ne olduğunu ve bir polinomun ortak faktörünün nasıl hesaplandığını bu bağlantıda görebilirsiniz.

İki polinomun çarpımı

Polinomları sayılarla ve tek terimlilerle nasıl çarpacağımızı öğrendikten sonra, bunun ne olduğunu ve polinomları polinomlarla nasıl çarpacağımızı görelim.

Polinomları çarpmak için şu adımları izleyin:

Birinci polinomdaki her terimi ikinci polinomdaki tüm terimlerle çarpın.
Aynı dereceye sahip tek terimlileri (benzer tek terimlileri) ekleyin (veya çıkarın).

Bu yöntemin tam olarak ne olduğunu görebilmeniz için, aşağıdaki polinom çarpımını adım adım çözeceğiz:

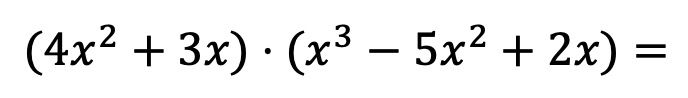
Her şeyden önce, birinci çarpım polinomunun her elemanını ikinci polinomun her terimiyle çarpmamız gerekir:

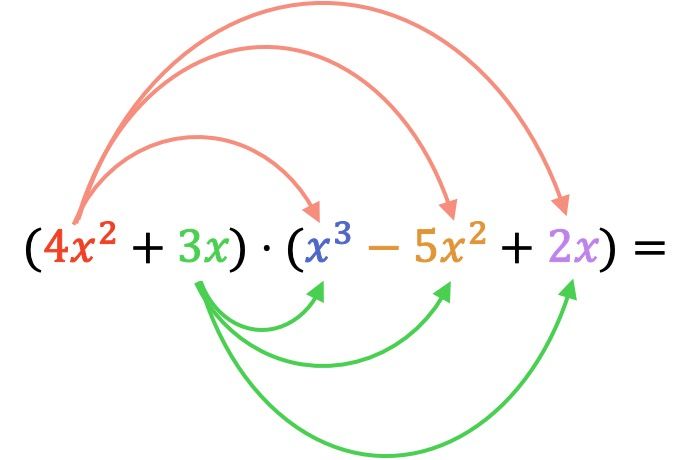
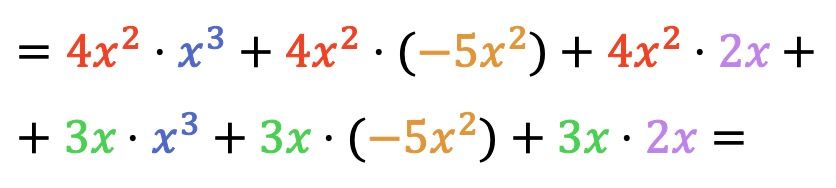
Şimdi tek terimlilerin tüm çarpımlarını yapıyoruz:

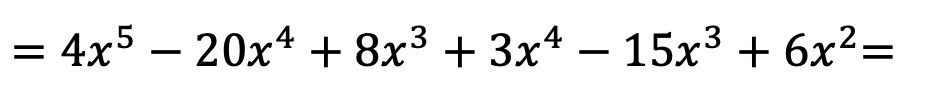
Polinomları birbiriyle çarptığımızda, ortaya çıkan benzer terimleri, yani aynı harfe ve aynı üste sahip terimleri gruplandırmamız gerekir:

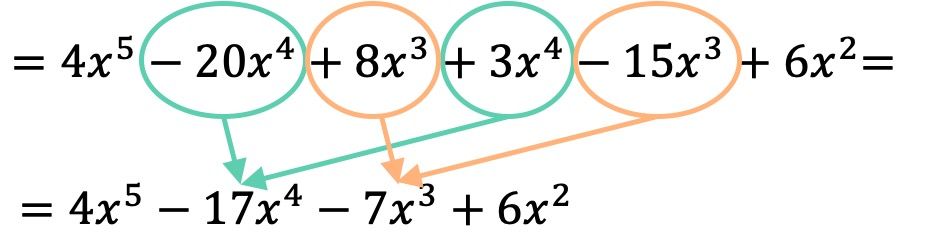
Dolayısıyla polinom çarpımının sonucu şu şekildedir:

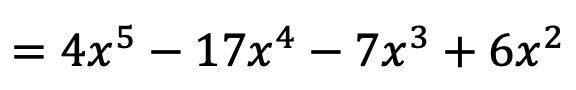
Ve bu şekilde polinomların çarpımını zaten hesapladık. Belki şu an size çok zor geliyor ama iki veya üç egzersizle pratik yaptığınızda çok daha kolay olacağını göreceksiniz.

Artık iki polinom arasındaki çarpımın nasıl çözüldüğünü gördüğünüze göre, muhtemelen polinomların nasıl bölüneceğini bilmek ilginizi çekiyordur. Aslında polinomları bölmek, çarpmaktan çok daha karmaşıktır, bu yüzden işlemi (ve ipuçlarını😉) adım adım açıkladık, böylece tam olarak anlayabilirsiniz. Eğer ilgileniyorsanız polinomların nasıl bölündüğünü görmek için bu bağlantıya tıklayın.

Dikey polinom çarpımı

Az önce bir polinomun başka bir polinomla yatay olarak nasıl çarpılacağını gördük, ancak bu daha klasik bir şekilde de yapılabilir: polinomları dikey olarak çarpın. Bir polinom çarpımı örneğini çözerek bu yöntemin nasıl kullanıldığını görelim.

Aşağıdaki iki polinomu dikey olarak çarpmak istersek:

$(5x^2+3x-4) \cdot (2x^2-x)$

Yapmamız gereken ilk şey, polinomların cebirsel çarpımı olarak bir polinomu diğerinin altına yerleştirmektir:

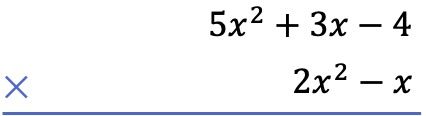
İkinci olarak, aşağıdaki polinomun her terimini yukarıdaki polinomun her terimiyle çarpıyoruz ve sonuçları en yüksek dereceden en düşük dereceye kadar sütunlar halinde sıralıyoruz:

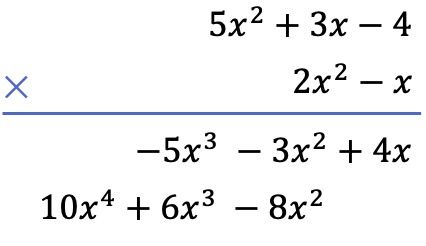
Ve son olarak dikey olarak hizalanmış terimleri ekliyoruz:

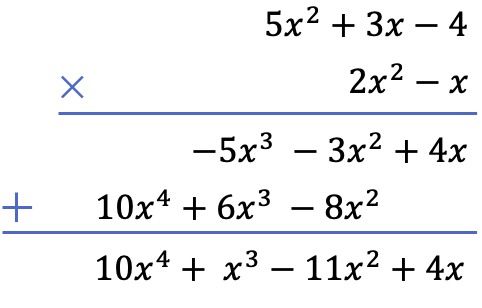
Artık polinomların çarpımını çözmek için mevcut 2 yöntemi gördüğünüze göre, kesirleri polinomlarla da çarpabileceğinizi biliyor muydunuz ? Üstelik bu kesirlerle sadece çarpma değil her türlü işlem yapılabilmektedir. Bu bağlantıya tıklayın ve cebirsel kesirlerin ne olduğunu öğrenin.

Polinom çarpımının özellikleri

Polinomların çarpımı aşağıdaki özelliklere sahiptir:

Değişme özelliği : Çarpan polinomların sırası çarpma sonucunu değiştirmez.

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

İlişkisel özellik : Üç veya daha fazla polinom çarpıldığında, faktörlerin nasıl gruplandırıldığına bakılmaksızın çarpım sonucu aynıdır:

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

Dağılım özelliği : iki polinomun toplamının üçte biriyle çarpımı, her toplamanın toplamının üçüncü polinomla çarpımına eşittir.

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

İki polinomun çarpımından elde edilen polinomun derecesi, çarpılan iki polinomun derecelerinin toplamına eşittir.

Polinomların çarpımı ile ilgili çözülmüş alıştırmalar

Pratik yapabilmeniz için size polinomların çarpımıyla ilgili birkaç çözülmüş alıştırma bırakıyorum. Bunları kendiniz çözmeye çalışabilir ve sonuçlarınızı önerilen çözümle kontrol edebilirsiniz. Daha sonra tüm sorularınızı yorumlardan bize sorabilirsiniz, size yardımcı olmaktan mutluluk duyarız.

1. Egzersiz

Polinomlar ve skalerler arasında aşağıdaki çarpımları hesaplayın:

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

Çözümü görün

Bir polinomun bir sayıyla çarpımını hesaplamak için sayıyı polinomun her bir öğesinin katsayısıyla çarpmanız gerekir. BU YÜZDEN:

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

Alıştırma 2

Polinomlar ve monomiyaller arasındaki aşağıdaki çarpımları çözün:

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

Çözümü görün

Bir polinomun bir tek terimle çarpımını çözmek için, söz konusu tek terimliyi polinomun her terimiyle çarpmanız gerekir. BU YÜZDEN:

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

Alıştırma 3

Polinomlar arasında aşağıdaki çarpmaların sonucunu belirleyin:

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

Çözümü görün

İki polinomun çarpımını hesaplamak için, birinci polinomun her elemanını ikinci polinomun her elemanıyla çarpmamız ve ardından benzer terimleri birlikte gruplandırmamız gerekir. BU YÜZDEN:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

Alıştırma 4

Polinomlar arasında aşağıdaki çarpmaların sonucunu bulun:

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

Çözümü görün

İki polinomun çarpımını hesaplamak için, birinci polinomun her elemanını ikinci polinomun her elemanıyla çarpmamız ve ardından benzer terimleri toplamamız gerekir. BU YÜZDEN:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

Alıştırma 5

Aşağıdaki polinom çarpımlarını hesaplayın:

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

Çözümü görün

2 polinomun çarpımını yapmak için, birinci polinomun her terimini ikinci polinomun her terimiyle çarpmanız, ardından elde edilen benzer monomları gruplamanız gerekir. Henüz:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

Alıştırma 6

Aşağıdaki 3 polinomun çarpımını çözün:

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

Çözümü görün

Problemin işleyişi polinomların 2 çarpımından, daha doğrusu iki binom ve bir trinomiyalden oluşur. Bu yüzden önce bir çarpım bulmamız ve ardından sonucu kalan polinomla çarpmamız gerekiyor.

Bu nedenle ilk çarpımı hesaplıyoruz:

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

Şimdi kalan çarpımı çözüyoruz:

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

Egzersiz 7

Aşağıdaki polinomları rasyonel katsayılarla (kesirlerle) çarpın:

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

Çözümü görün

Polinomların kesirleri olmasına rağmen yine de iki polinomun çarpımıdır. Bu nedenle herhangi bir polinom çarpımı gibi çözülmesi gerekir: tüm elemanları birlikte çarpın ve ardından benzer tek terimlileri gruplandırın.

Bu nedenle polinomları çarpıyoruz:

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

Ve son olarak, değişmez kısımları aynı olan terimleri ekliyoruz (ya da çıkarıyoruz):

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

Bu alıştırmayı başarıyla tamamlamak için kesirlerle ilgili işlemlerde uzmanlaşmanız önemliydi. Ancak herhangi bir adımla ilgili sorularınız varsa yorumlarda sorabilirsiniz ve mümkün olan en kısa sürede cevaplayacağız.

Polinomların çarpımı (veya çarpımı)

Bir polinomu bir sayıyla çarpma

Bir polinomun bir tek terimle çarpılması

İki polinomun çarpımı

Dikey polinom çarpımı

Polinom çarpımının özellikleri

Polinomların çarpımı ile ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Egzersiz 7

Yorum bırakın Yanıtı iptal et