Polinomlar Nasıl Çarpanlarına Ayrılır (Polinom Faktoringi) -

Bu sayfada herhangi bir polinom türünün nasıl çarpanlara ayrılacağını açıklıyoruz. İlk olarak bir polinomun Ruffini kuralıyla nasıl çarpanlara ayrıldığını göreceğiz, ardından bağımsız terimi olmayan polinomların nasıl çarpanlara ayrıldığına geçeceğiz, ardından kesirli kök polinomların çarpanlara ayrılmasını ve son olarak da çarpanlara ayırmanın özel durumlarını analiz edeceğiz (dikkate değer) kimlikler, gruplandırma yoluyla çarpanlara ayırma, üç terimli sayılar vb.). Tüm açıklamalar örneklerle yapılmıştır ve ayrıca sonunda polinomları çarpanlarına ayırma konusunda adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Polinom çarpanlarına ayırma nedir?

Polinom çarpanlara ayırma, matematikte bir polinomu faktörlerin çarpımına ayırmak için kullanılan bir tekniktir.

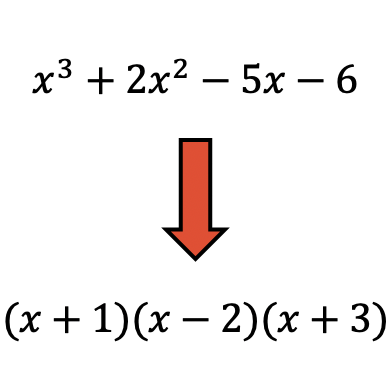
çarpanlara ayırma polinomları (çarpanlara ayırma polinomları)

Çarpanlarına ayırma polinomları çok kullanışlıdır çünkü çarpanlarına ayrılan polinomlarla işlem yapmak daha kolaydır.

Artık polinom çarpanlarına ayırmanın ne olduğunu bildiğimize göre, polinomların nasıl çarpanlara ayrıldığını görelim.

Ruffini kuralıyla polinomları çarpanlarına ayırma

Açıkçası, bir polinomun Ruffini kuralıyla nasıl çarpanlara ayrılacağını anlamak için öncelikle Ruffini kuralının nasıl uygulanacağını bilmeniz gerekir. Bu nedenle, öncelikle prosedürün nasıl göründüğünü gözden geçirmek isterseniz diye size bu bağlantıyı bırakıyoruz.

Bir polinomu çarpanlarına ayırmak için aşağıdaki adımlar izlenmelidir:

Polinomun kökleri Ruffini kuralına göre hesaplanır.
x=a türünde bulunan her bir kök, bir (xa) faktörü biçiminde ifade edilir.
Çarpanlarına ayrılmış polinom, bulunan tüm faktörlerin, ağırlıklandırılmamış polinomun en yüksek dereceli teriminin katsayısı ile çarpımının ürünüdür.

Bunun nasıl yapıldığını görebilmeniz ve polinomları çarpanlara ayırma prosedürünü daha iyi anlayabilmeniz için aşağıda adım adım açıklanan somut bir örnek bulacaksınız:

Aşağıdaki polinomu çarpanlarına ayırın:

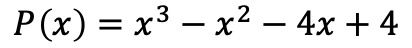
Yapılacak ilk şey polinomun köklerini veya sıfırlarını hesaplamaktır. Bunu yapmak için polinomun bağımsız teriminin bu durumda ±1, ±2 ve ±4 olan bölenlerini bulmamız gerekir.

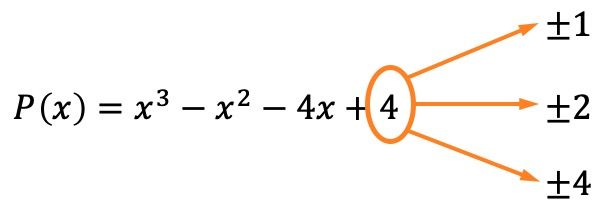
Artık kalan ve faktörler teoremi sayesinde biliyoruz ki, polinomun bu değerlerden birine bölümünden kalan kısım 0’a eşitse bu, söz konusu değerin polinomun bir kökü olduğu anlamına gelir.

Bu nedenle polinomu Ruffini kuralına göre bağımsız terimin bölenlerinin her birine bölmemiz ve hangi durumlarda kalanın sıfır olduğunu görmemiz gerekir.

Örneğin, Ruffini kuralını şu şekilde uygulayarak başlıyoruz:

$x=+1:$

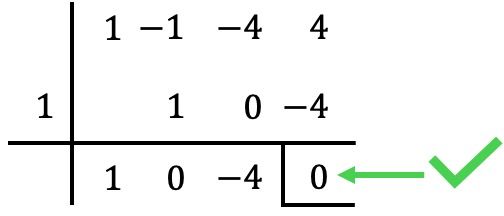
Bu durumda bölmenin geri kalanı (veya kalıntısı) sıfırdır, yani

$x=1$

Polinomun bir köküdür. ✅

Mükemmel, elimizde zaten polinomun bir kökü var, geriye kalan tek şey kalan diğer kökleri belirlemek. Bunu yapmak için bağımsız terimin başka bir böleniyle Ruffini kuralını kullanırız; örneğin

$x=-1.$

Ayrıca tamsayı polinomunda Ruffini yöntemini kullanmaya gerek yok ama bir önceki adımda kaldığımız yerden devam edebiliriz:

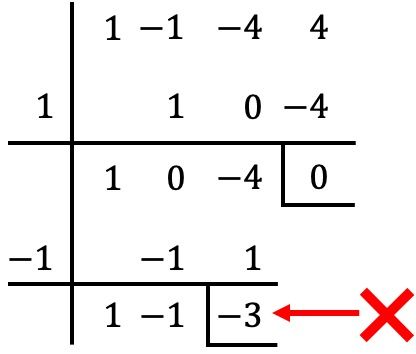
Ancak bu durumda bölme işlemi yapılırken

$x=-1$

elde edilen kalan 0’dan farklıdır, dolayısıyla

$x=-1$

Polinomun kökü değildir. ❌

Bu nedenle başka bir değer denemeliyiz, örneğin Ruffini kuralını şununla uyguluyoruz:

$x=+2:$

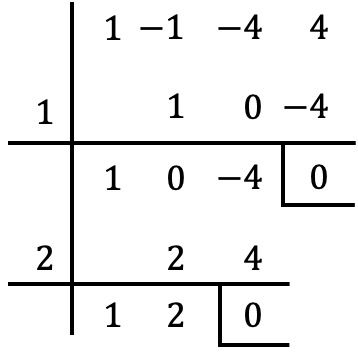
Bu durumda yine sıfır kalan elde ederiz, yani

$x=2$

Aynı zamanda polinomun da köküdür.

Ve aynı işlemi uygulamaya devam ediyoruz. Şimdi olup olmadığını kontrol ediyoruz

$x=-2$

polinomun kökü mü değil mi:

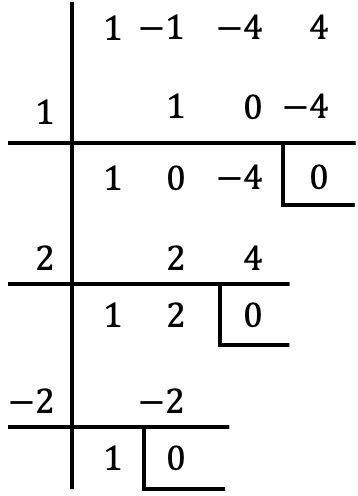
Bölerek

$x=-2$

Ruffini kuralıyla sıfır kalan elde ederiz, yani

$x=-2$

polinomun bir kökü veya sıfırıdır.

Bu nedenle artık Ruffini kuralını uygulamaya devam edemeyiz, dolayısıyla polinomun tüm köklerini zaten bulduk:

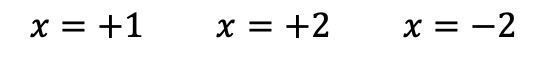
Polinomun tüm köklerini belirledikten sonra onu çarpanlara ayırabiliriz. Bunu yapmak için her kökü ifade etmeniz yeterlidir

$x=a$

tipin bir faktörü şeklinde

$(x-a)$

yani her kök için bir parantez koymanız gerektiği anlamına gelir

$x$

ve kökün işareti değişti:

Artık tüm kökleri faktörler olarak ifade ettiğimize göre, tüm parantezleri orijinal polinomun en yüksek dereceli teriminin katsayısıyla çarpmamız gerekir:

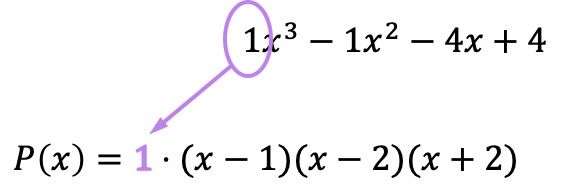
faktör polinomları en yüksek derece katsayısı

Her ne kadar bu durumda katsayı 1 olsa ve bu nedenle sonucu etkilemese de bu çarpma işlemini yapmayı unutmamak önemlidir. Çünkü söz konusu katsayı 1’den farklı olsaydı çarpanlara ayrılan polinom değişecek ve dolayısıyla sayıyı girmeyerek polinomu çarpanlara ayırmada hata yapmış olacaktık.

Kısaca çarpanlara ayrılmış polinom şu şekildedir:

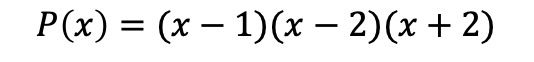
Bağımsız terimi olmayan polinomların çarpanlara ayrılması

Az önce bağımsız terimin polinomları çarpanlarına ayırmada önemli olduğunu gördük, çünkü polinomun olası köklerini belirlememize izin veriyor. Ancak bağımsız terimi olmayan bir polinomu nasıl çarpanlara ayırırsınız?

Bağımsız terimi olmayan bir polinomu çarpanlarına ayırmak için, önce polinomun ortak çarpanı çıkarılmalı, ardından Ruffini kuralı kullanılarak ortak faktör olmadan polinomun kökleri çıkarılmalıdır.

Bu şekilde yazıldığında biraz karmaşık gelebilir, bu yüzden bir örneği adım adım çözelim, böylece bir polinomu ortak çarpanlara nasıl ayıracağınızı görebilirsiniz:

Aşağıdaki polinomun faktöriyel ayrıştırmasını gerçekleştirin:

$P(x) = x^4-3x^3-x^2+3x$

Gördüğünüz gibi problemdeki polinomun bağımsız bir terimi yok, dolayısıyla polinomun ortak faktörünü almak zorundayız. Yakından bakarsak polinomun tüm elemanlarının en az bir tane olduğu görülür.

$x,$

yani ortak faktör

$x.$

Bu nedenle, polinomdan ortak faktörü çıkarırken aşağıdaki ifadeyi elde ederiz:

$P(x) = x\left(x^3-3x^2-x+3\right)$

Polinomun ortak faktörünü çıkardıktan sonra, parantez içinde gruplandırılmış polinomun köklerini hesaplamak için Ruffini kuralını uygularız (önceki bölümde gördüğümüz prosedürle):

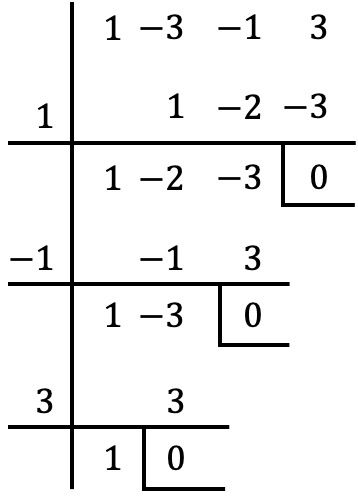
bağımsız terimi olmayan faktöriyel polinomlar

Dolayısıyla parantez içindeki polinomun kökleri veya sıfırları şöyledir:

$\bm{x=+1 \qquad x=-1 \qquad x=+3}$

Bu nedenle, polinomu çarpanlara ayırmak için, parantez içindeki polinomu, kökleri faktör biçiminde olacak şekilde değiştirin (yukarıdaki bölümde açıklandığı gibi):

$\begin{array}{c}P(x) = x\left(x^3-3x^2-x+3\right) \\[2ex]\color{red} \bm{\downarrow} \\[2ex] \bm{P(x) = x(x-1)(x+1)(x-3)}\end{array}$

Ve bu şekilde, derecesi 0 olmayan bir polinomu zaten çarpanlarına ayırmış olduk. Tek farkın, önce ortak bir çarpanı çıkarmamız gerektiği olduğunu unutmayın, ancak sonraki adımların tümü tamamen aynıdır.

Öte yandan şunu bilmelisin

$x=0$

Bu aynı zamanda polinomun bir köküdür, çünkü ortak faktörü çıkardığımızda, polinomun köklerinden birinin şöyle olduğunu ima eder:

$x=0.$

Yani polinomun tüm kökleri aşağıdaki gibidir:

$\bm{x= 0 \qquad x=+1 \qquad x=-1 \qquad x=+3}$

Aslında polinomun derecesinin gösterdiği kadar köke sahip olması gerekir. Bu durumda polinom 4. derecedendir ve dolayısıyla 4 kökü vardır.

Rasyonel kökleri olan polinomların çarpanlara ayrılması

Şu ana kadar tamsayı köklü polinomların çarpanlara ayrılması örneklerini gördük, ancak bir polinomun rasyonel kökleri, yani kesirli kökleri de olabilir. Bu tür polinom çarpanlara ayırmanın nasıl çözüldüğünü bir örnekle görelim:

Aşağıdaki eksik polinomu çarpanlarına ayırın:

$P(x) = 4x^3-7x+3$

Her zaman olduğu gibi, polinomun köklerini belirlemeye çalışmak için bağımsız terimin bölenleriyle birlikte Ruffini kuralını kullanıyoruz:

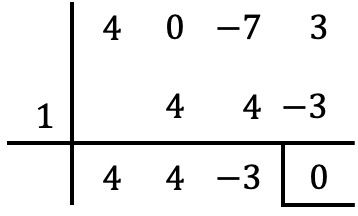
Rasyonel kökleri olan polinomların çarpanlara ayrılması

Ancak Ruffini ile daha fazla kök hesaplayamayız çünkü Ruffini’yi bağımsız terimin tüm diğer bölen sayılarıyla yapmaya çalışırsak sıfırdan farklı bir kalan elde ederiz.

Bu nedenle kendimizi yalnızca

$x=1$

bölümün geri kalanı 0’a eşittir; bu, polinomun kesirli köklere sahip olabileceği anlamına gelir. Bu kökleri belirlemek için Ruffini’yi kesirlerle uygulayabiliriz, ancak hesaplamalarda hata yapmak çok kolaydır ve bu nedenle bu durumlarda genellikle aşağıdakileri yaparız:

Ruffini kuralını tamsayı kökleriyle uygulamaya devam edemediğimizde, elde edilen son polinomu 0’a eşitlemeli ve ortaya çıkan denklemi çözmeliyiz. Yani polinomun kökleri denklemden bulunan değerler olacaktır.

Öte yandan, denklemin çözümü yoksa bu, polinomun artık köklerinin olmadığı ve dolayısıyla tamamen çarpanlara ayrılamayacağı anlamına gelir.

Bu nedenle bölüm polinomunu sıfıra eşitliyoruz:

$4x^2+4x-3=0$

Ortaya çıkan denklemi çözmek için ikinci dereceden denklem formülünü kullanırız:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-4 \pm \sqrt{4^2-4\cdot 4\cdot (-3)}}{2\cdot 4}= \cfrac{-4\pm \sqrt{16+48}}{8} = \cfrac{-4 \pm\sqrt{64}}{8}$

$\displaystyle x = \cfrac{-4 \pm 8}{8} = \begin{cases} \cfrac{-4+8}{8} = \cfrac{4}{8} = \cfrac{1}{2} \\[4ex]\cfrac{-4-8}{8} = \cfrac{-12}{8} = -\cfrac{3}{2} \end{cases}$

Dolayısıyla polinomun kökleri şöyledir:

$x=+1 \qquad x=\cfrac{1}{2} \qquad x=-\cfrac{3}{2}$

Dolayısıyla polinomun kesir şeklinde kökleri vardır.

Polinomun tüm köklerini bildiğimizde, her bir kökü ifade ederek çarpanlara ayrılmış polinomu kolayca bulabiliriz.

$x=a$

tipin bir faktörü şeklinde

$(x-a)$

yani her kök için bir parantez koymanız gerektiği anlamına gelir

$x$

ve kökün işareti değişti:

$\displaystyle P(x)= 4\left(x-1\right)\left(x-\frac{1}{2}\right)\left(x+\frac{3}{2}\right)$

Bir polinomu çarpanlarına ayırmak için çarpanlarını çarpanlara ayrılmamış polinomun en yüksek dereceli teriminin katsayısıyla çarpmanız gerektiğini unutmayın; bu durumda bu değer 4’tür.

Polinomların çarpanlarına ayrılmasının özel durumları

Normalde, yukarıda açıklandığı gibi bir polinomu çarpanlara ayırmak için Ruffini kuralı (veya sentetik bölme) kullanılır. Ancak problemin polinomuna bağlı olarak bazen polinom çarpanlarına ayırmayı daha hızlı yapabilirsiniz. Aşağıda bu özel durumların her birini göreceğiz.

Önemli kimlikleri faktoring

Bir polinomun kayda değer bir kimliğe (veya dikkate değer bir çarpıma) karşılık geldiğini görürsek, onu çarpanlara ayırmak çok kolaydır. Ancak bunu yapabilmek için tanınmış kimliklerin formüllerine hakim olmanız gerekir, aksi takdirde bu bağlantıya bir göz atmanızı tavsiye ederim, burada sadece formülleri değil, aynı zamanda tanınmışların örneklerini de görebileceksiniz. kimlikleri ve onlarla adım adım çözülen alıştırmalar bile yapabilirsiniz.

Karelerin farkı

Bildiğiniz gibi kareler farkının dikkate değer özdeşliğinin formülü şu şekildedir:

$a^2-b^2=(a+b)\cdot (a-b)$

Bu nedenle, ifadeyi karşılayan bir polinom bulursak

$a^2-b^2$

doğrudan dikkate alınabilir.

Kareler farkının dikkate alındığı aşağıdaki örneğe bakın:

$x^2-9 = (x+3)(x-3)$

Öte yandan polinomun kökleri:

$x=-3 \qquad x=+3$

Kareler farkı olan binomların çarpanlara ayrılmasına ilişkin diğer örnekler:

$x^2-4=(x+2)(x-2) \quad \longrightarrow \quad \text{ra\'ices: } x=-2, +2$

$x^2-16=(x+4)(x-4) \quad \longrightarrow \quad \text{ra\'ices: } x=-4, +4$

$x^2-25=(x+5)(x-5) \quad \longrightarrow \quad \text{ra\'ices: } x=-5, +5$

Toplama ve çıkarma karesi

Kalan 2 önemli kimliğin formüllerini zaten biliyor olmalısınız: toplama karesi ve çıkarma karesi.

Toplam Kare

$a^2+2ab+b^2 = (a+b)^2$

Çıkarma karesi

$a^2-2ab+b^2= (a-b)^2$

Dolayısıyla, bir polinomun bu iki önemli kimlikten birine karşılık geldiğini fark edersek, onu doğrudan çarpanlara ayırabiliriz. Aşağıdaki örneklere bakın:

$x^2+6x+9 = (x+3)^2$

Çift kök:

$x=-3$

$x^2-8x+16 = (x-4)^2$

Çift kök:

$x=4$

Bu dikkate değer ürün türlerini belirlemek biraz daha zordur. İşin püf noktası, polinomun bağımsız teriminin bir sayının karesi olup olmadığını ve daha yüksek dereceli terimin bir monomiyalin karesi olup olmadığını kontrol etmektir (genellikle

$x$

), bu durumda, bunun doğru olduğunu doğrulamak yeterlidir.

$2ab$

ara diplomanın sonuna eşittir.

Örneğin, aşağıdaki polinomumuz varsa:

$x^2+10x+25$

Bu durumda polinomun tüm elemanları pozitif olduğundan, bu yalnızca bir toplamın karesi olabilir. Yani değişken

$b$

Bağımsız terimin kökü olduğundan formülün 5 olması gerekir ve değişken

$a$

olmalı

$x$

, çünkü may derecesi teriminin köküdür.

$a=\sqrt{x^2} = x$

$b=\sqrt{25} = 5$

Şimdi yapmamız gereken tek şey, toplamın karesi formülünün ara dereceli terimle karşılandığını kanıtlamak:

$2ab = 10x \ \color{blue} \bm{?}$

$2ab = 2\cdot x \cdot 5 = 10 x$

✅

Dikkate değer çarpımın formülü karşılanmıştır, dolayısıyla çarpanlara ayrılmış polinom şu şekildedir:

$x^2+10x+25 = (x+5)^2$

Ve bu polinomun kökü

$x=-5,$

bu bir çift köktür çünkü çarpanı karedir (iki kez tekrarlanır).

Aşağıda tam kare üç terimlileri çarpanlara ayırmaya ilişkin daha fazla örnek verilmiştir:

$x^2-4x+4=(x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+2$

$x^2+14x+49=(x+7)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=-7$

$9x^2-12x+4=(3x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+\cfrac{2}{3}$

İkinci derece trinomiallerin çarpanlara ayrılması

Az önce gördüğümüz gibi, bazen tam kare olan üç terimli sayılar vardır ve bunlar doğrudan dikkate değer özdeşlik formülleriyle çarpanlara ayrılabilir. Ancak trinomiyallerin çoğu kayda değer çarpımlar değildir, peki polinomların bu durumlarını nasıl çarpanlara ayırıyoruz?

İkinci dereceden bir polinomu çarpanlara ayırmak için Ruffini yöntemini uygulamak gerekli değildir; sadece polinomu sıfıra eşitleyin ve elde edilen ikinci dereceden denklemi çözün. Dolayısıyla denklemin çözümleri polinomun kökleri olacaktır.

Örneğin, aşağıdaki 2. derece polinomunu çarpanlarına ayırmamız istenirse:

$P(x) = x^2+2x-15$

Ruffini kullanmak yerine polinomu 0’a eşitliyoruz:

$x^2+2x-15=0$

Şimdi denklemin çözümlerini bulmak için 2. derece denklemin formülünü kullanıyoruz:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-2 \pm \sqrt{2^2-4\cdot 1\cdot (-15)}}{2\cdot 1}= \cfrac{-2\pm \sqrt{4+60}}{2} = \cfrac{-2 \pm\sqrt{64}}{2}$

$\displaystyle x = \cfrac{-2 \pm 8}{2} = \begin{cases} \cfrac{-2+8}{2} = \cfrac{6}{2} = 3 \\[4ex]\cfrac{-2-8}{2} = \cfrac{-10}{2} = -5 \end{cases}$

Dolayısıyla polinomun kökleri şöyledir:

$x=3 \qquad x=-5$

Ve son olarak polinom çarpanlara ayırma:

$P(x) =(x-3)(x+5)$

Çift üslü dördüncü derece trinomiallerin çarpanlara ayrılması

Önceki durumda olduğu gibi, çift üslü dördüncü dereceden bir polinomu çarpanlara ayırmak için polinomu sıfıra eşitlememiz ve çift kare denklemini çözmemiz gerekir. Böylece bulunan değerler polinomun köklerine karşılık gelir.

Örnek olarak aşağıdaki 4. derece polinomunu çarpanlarına ayıracağız:

$P(x) =x^4-5x^2+4$

İlk olarak polinomu sıfıra eşitliyoruz:

$x^4-5x^2+4=0$

Şimdi çift kare denklemini çözmemiz gerekiyor. Bunu yapmak için değişken değişikliği yapıyoruz:

$x^2=t$

$t^2-5t+4=0$

İkinci dereceden denklemi aşağıdaki formülle çözüyoruz:

$t= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$t= \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1}= \cfrac{5\pm \sqrt{25-16}}{2} = \cfrac{5 \pm\sqrt{9}}{2}$

$\displaystyle t = \cfrac{5 \pm 3}{2} = \begin{cases} \cfrac{5+3}{2} = \cfrac{8}{2} = 4 \\[4ex]\cfrac{5-3}{2} = \cfrac{2}{2} = 1 \end{cases}$

Kökleri hesaplamak için değişken değişikliğini iptal ederiz:

$x^2=t$

$x^2=4$

$x=\sqrt{4}$

$x=\pm 2$

$x^2=1$

$x=\sqrt{1}$

$x=\pm 1$

Dolayısıyla polinomun kökleri şöyledir:

$x=+2 \qquad x=-2 \qquad x=+1 \qquad x=-1$

Polinomun köklerini veya sıfırlarını bildiğimizde, köklerini cebirsel olarak faktörler biçiminde ifade ederek onu çarpanlara ayırırız:

$P(x) =(x-1)(x+1)(x-2)(x+2)$

Polinomları gruplandırarak çarpanlara ayırma

Bazı çok özel durumlarda, çok özel bir polinom tipini çarpanlara ayırmak için bir formül kullanılabilir.

Aşağıdaki formda bir polinomumuz varsa:

$x^2-ax- bx+ab$

Ortak çarpanı çıkararak polinomu basitleştirebiliriz:

$x^2-ax- bx+ab = x(x-a)-b(x-a)$

Ve polinom, ortak faktörün ikinci kez çıkarılmasıyla daha da basitleştirilebilir:

$x(x-a)-b(x-a) =(x-a)\cdot (x-b)$

Bu şekilde, Ruffini veya başka bir yöntem uygulamadan polinomu çarpanlarına ayırmayı başardık. Ve söz konusu polinomun kökleri şöyle olacaktır:

$x=a \qquad x=b$

Şimdi bu yöntemi sayısal bir örnekle görelim:

$x^2-3x-2x+6$

Öncelikle ortak çarpanı kaldırıyoruz.

$x$

ve 2 ile:

$x^2-3x-2x+6 = x(x-3)-2(x-3)$

Ve şimdi olduğu gibi

$(x-3)$

polinomun ortak çarpanı ise, ortak çarpanını çıkarıyoruz

$(x-3):$

$x(x-3)-2(x-3)=(x-3)\cdot (x-2)$

Dolayısıyla polinomun kökleri şöyledir:

$x=3 \qquad x=2$

Bu yöntem aynı zamanda polinomların çift ortak faktör çıkarımı yoluyla çarpanlara ayrılması olarak da adlandırılır. Bu çok hızlı bir prosedür olmasına rağmen, bu yöntemle çarpanlara ayırma sırasında hatalar sıklıkla bildirildiğinden bu tür çarpanlara ayırma işlemini yapmanızı önermiyoruz. Ek olarak, yukarıda gördüğümüz gibi, 2. derecedeki bir polinom da basit bir ikinci dereceden denklem çözülerek çarpanlara ayrılabilir. Kısacası bu yöntemi iyi anlamazsanız hiçbir şey olmaz.

Son olarak, LLL algoritması, Kronecker yöntemi ve Trager yöntemi gibi matematiksel güçlükleri nedeniyle burada açıklanmayan başka daha karmaşık polinom çarpanlara ayırma yöntemlerinin de bulunduğunu belirtmek gerekir.

Polinomları çarpanlara ayırmaya ilişkin çözülmüş alıştırmalar

Çarpanlara ayırma polinomlarının tüm türlerini gördükten sonra, alıştırmaları çözmeye çalışmanızı öneririz. Bu nedenle aşağıda polinomları çarpanlarına ayırmaya yönelik birkaç adım adım çözülmüş alıştırmalar hazırladık. Unutmayın, sorularınız varsa yorumlara yazabilirsiniz, hızlı bir şekilde cevaplayacağız.

1. Egzersiz

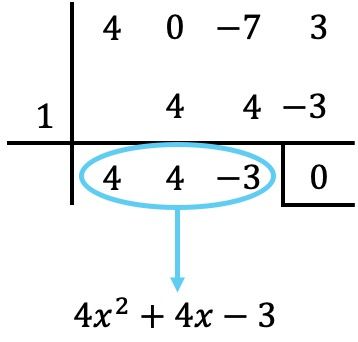
Aşağıdaki 3. derece polinomun çarpanlarına ayırma işlemini gerçekleştirin:

$P(x)=x^3-3x^2-6x+8$

Çözümü görün

Tam, sıralı, üçüncü dereceden ve sonuçta bağımsız bir polinomdur. Bu nedenle polinomun köklerini belirlemek için Ruffini yöntemini uyguluyoruz:

Polinomları çarpanlarına ayırmak için adım adım alıştırmalar

Dolayısıyla polinomun kökleri aşağıdaki gibidir:

$x=+1 \qquad x=-2 \qquad x=+4$

Bu nedenle polinom çarpanlara ayırma şu şekildedir:

$P(x)= 1 \cdot (x-1)\cdot (x+2) \cdot (x-4)$

$\bm{P(x)= (x-1)(x+2)(x-4)}$

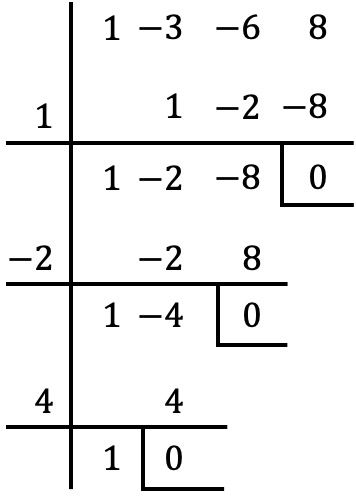
Alıştırma 2

Aşağıdaki 4. derece polinomun çarpanlarına ayrılmasını hesaplayın:

$P(x)=x^4+x^3-7x^2-x+6$

Çözümü görün

Bu dördüncü dereceden bir polinomdur ve bağımsız bir terime sahiptir, bu nedenle polinomun köklerini bulmak için Ruffini yöntemini kullanırız:

polinom çarpanlara ayırma egzersizleri pdf

Dolayısıyla polinomun kökleri şöyledir:

$x=+1 \qquad x=-1 \qquad x=2 \qquad x=-3$

Polinomu çarpanlara ayırdığımızda elimizde şu kalır:

$P(x)= 1 \cdot (x-1)\cdot (x+1)\cdot (x-2) \cdot (x+3)$

$\bm{P(x)= (x-1)(x+1)(x-2)(x+3)}$

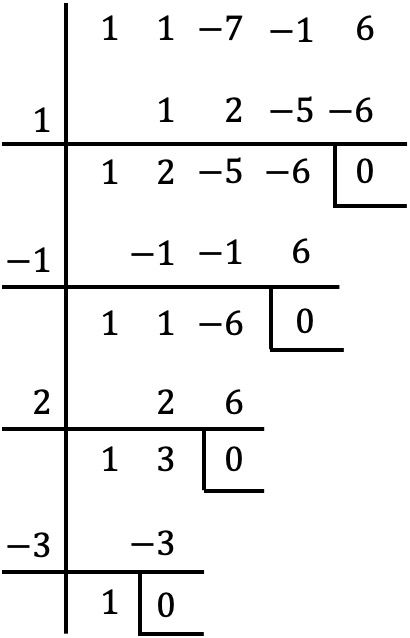
Alıştırma 3

Aşağıdaki dördüncü derece polinomun çarpanlara ayrılmasını bulun:

$P(x)=x^4-2x^3-13x^2-10x$

Çözümü görün

Bu durumda polinomun bağımsız terimi yoktur, önce ortak çarpanı çıkarmamız gerekir:

$P(x)=x(x^3-2x^2-13x-10)$

Artık x’in ortak faktörünü aldığımıza göre, parantez içindeki polinomun köklerini veya sıfırlarını Ruffini yöntemini kullanarak hesaplıyoruz:

Ruffini polinomlarının çarpanlara ayrılması çözümlü alıştırmalar pdf

Dolayısıyla polinomun kökleri, Ruffini yöntemiyle bulduğumuz kökler artı ortak faktörün x=0’ıdır:

$x=0 \qquad x=-1 \qquad x=-2 \qquad x=5$

Ve son olarak polinomu faktörlere ayrıştırarak aşağıdaki ifadeyi elde ederiz:

$P(x)= 1 \cdot x \cdot (x+1)\cdot (x+2)\cdot (x-5)$

$\bm{P(x)= x(x+1)(x+2)(x-5)}$

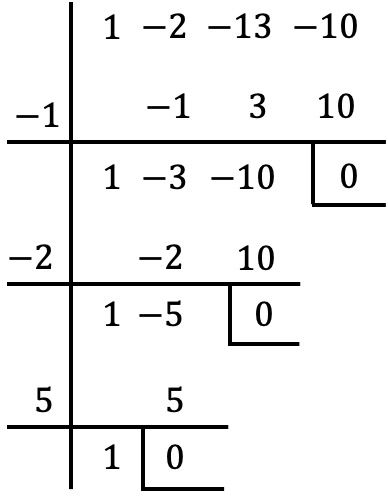
Alıştırma 4

Aşağıdaki üçüncü derece polinomu faktörlere dönüştürün:

$P(x)=6x^3+25x^2+21x-10$

Çözümü görün

Bu polinomun bağımsız bir terimi vardır, bu nedenle köklerini Ruffini algoritmasıyla hesaplıyoruz:

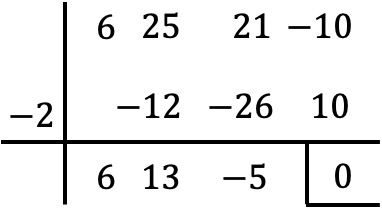
2. satırda 3. derecenin faktöriyel polinomları

Ancak bu noktaya geldiğimizde Ruffini kuralını uygulamaya devam edemeyiz çünkü başka bir tam sayı olmadan bölümün geri kalanı sıfırdır.

Bu nedenle elde edilen polinomu sıfıra eşitliyoruz:

$6x^2+13x-5=0$

Ortaya çıkan denklemi çözmek için ikinci dereceden denklem formülünü uyguluyoruz:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-13 \pm \sqrt{13^2-4\cdot 6\cdot (-5)}}{2\cdot 6}= \cfrac{-13\pm \sqrt{169+120}}{12} = \cfrac{-13 \pm\sqrt{289}}{12}$

$\displaystyle x = \cfrac{-13 \pm 17}{12} = \begin{cases} \cfrac{-13+17}{12} = \cfrac{4}{12} = \cfrac{1}{3} \\[4ex]\cfrac{-13-17}{12} = \cfrac{-30}{12} = -\cfrac{5}{2} \end{cases}$

Dolayısıyla polinomun kökleri veya sıfırları şöyledir:

$x=-2 \qquad x=\cfrac{1}{3} \qquad x=-\cfrac{5}{2}$

Bu nedenle polinomun çarpanlarına ayrılması kesirlerle yapılmalıdır:

$\displaystyle P(x)= 6\left(x+2\right)\left(x-\frac{1}{3}\right)\left(x+\frac{5}{2}\right)$

Alıştırma 5

Aşağıdaki 6. derece polinomun çarpanlara ayrılmasını belirleyin:

$P(x)=x^6-3x^5+14x^3-12x^2$

Çözümü görün

Problemdeki polinomun bağımsız bir terimi yoktur, dolayısıyla ilk önce ortak çarpanı çıkarmalıyız ki bu durumda bu

$x^2:$

$P(x)=x^2(x^4-3x^3+14x-12)$

Polinomdan ortak faktörü çıkardıktan sonra, Ruffini kuralını kullanarak polinomun köklerini parantez içinde buluruz:

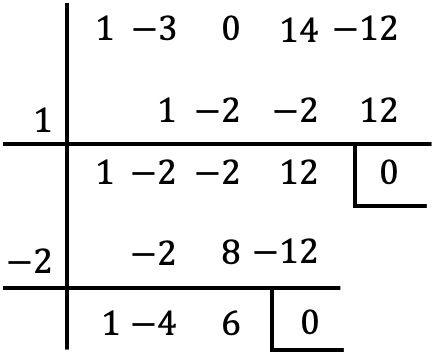
benzersiz polinomların çarpanlara ayrılması

Ancak bu aşamaya geldiğimizde ilerlemeye devam edemeyiz çünkü başka bir tam sayı olmadan kalan sıfırdır.

Bu nedenle elde edilen polinomu sıfıra eşitliyoruz:

$x^2-4x+6=0$

Ve ikinci dereceden denklemi aşağıdaki formülle çözüyoruz:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1\cdot 6}}{2\cdot 1}= \cfrac{4\pm \sqrt{16-24}}{2} = \cfrac{4 \pm\sqrt{-8}}{2} \ \color{red} \bm{\times}$

Negatif sayıların kökleri yoktur, dolayısıyla denklemin çözümü yoktur, bu da polinomun daha fazla kökünü bulamayacağımız anlamına gelir. Başka bir deyişle polinom tamamen çarpanlara ayrılamaz.

Ancak bulabildiğimiz kökler şunlardır:

$x=0 \qquad x=0 \qquad x=1 \qquad x=-2$

Kök olduğuna dikkat edin

$x=0$

iki kez tekrarlanıyor çünkü ortak çarpanı kaldırdık

$x^2,$

ve karesi olduğundan bu onun çift kök olduğu anlamına gelir.

Sonuç olarak, çarpanlara ayrılmış polinom, faktörler olarak ifade edilen bulunan tüm köklerin çarpımı olacaktır.

$(x-a)$

Ruffini kuralından elde edilen ve daha fazla dikkate alınamayan polinomla çarpılır:

$P(x)= 1 \cdot x^2 \cdot (x-1)\cdot (x+2)\cdot (x^2-4x+6)$

$\bm{P(x)= x^2(x-1)(x+2)(x^2-4x+6)}$

Alıştırma 6

Aşağıdaki polinomların tümünün çarpanlarına ayırma işlemlerini gerçekleştirin:

$\text{A)} \ P(x)=x^2 + 12x+36$

$\text{B)} \ Q(x)=x^2 -64$

$\text{C)} \ R(x)=x^2 - 18x+81$

$\text{D)} \ S(x)=x^2+10x+24$

Çözümü görün

A) bölümündeki polinom dikkate değer bir kimliğe, özellikle de toplamın karesine karşılık gelir. Bu nedenle çarpanlara ayrılması şu şekildedir:

$P(x)=x^2 + 12x+36 = \bm{(x+6)^2}$

B) bölümünün polinomu da dikkate değer bir çarpımdır, özellikle karelerin farkıdır, dolayısıyla:

$Q(x)=x^2 -64 = \bm{(x+8)(x-8)}$

Benzer şekilde, C) bölümündeki polinom dikkate değer bir eşitliktir, özellikle bir çıkarmanın karesinden oluşur. Bu nedenle çarpanlara ayrılması şu şekildedir:

$R(x)=x^2 - 18x+81 = \bm{(x-9)^2}$

Son olarak D) kısmındaki polinom dikkate değer bir özdeşlik değildir. Bu nedenle polinomu 0’a eşitlemeli ve köklerini bulmak için elde edilen denklemi çözmeliyiz:

$x^2+10x+24 =0$

İkinci dereceden denklem formülünü kullanıyoruz:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-10 \pm \sqrt{10^2-4\cdot 1\cdot 24}}{2\cdot 1}= \cfrac{-10\pm \sqrt{100-96}}{2} = \cfrac{-10 \pm\sqrt{4}}{2}$

$\displaystyle x = \cfrac{-10 \pm 2}{2} = \begin{cases} \cfrac{-10+2}{2} = \cfrac{-8}{2} = -4 \\[4ex]\cfrac{-10-2}{2} = \cfrac{-12}{2} = -6\end{cases}$

Dolayısıyla D) polinomunun kökleri şöyledir:

$x=-4 \qquad x=-6$

Ve son olarak polinom çarpanlara ayırmanın sonucu:

$\bm{S(x)=(x+4)(x+6)}$

Polinomlar nasıl faktoringe alınır (polinom faktoringi)

Polinom çarpanlarına ayırma nedir?

Ruffini kuralıyla polinomları çarpanlarına ayırma

Bağımsız terimi olmayan polinomların çarpanlara ayrılması

Rasyonel kökleri olan polinomların çarpanlara ayrılması

Polinomların çarpanlarına ayrılmasının özel durumları

Önemli kimlikleri faktoring

Karelerin farkı

Toplama ve çıkarma karesi

İkinci derece trinomiallerin çarpanlara ayrılması

Çift üslü dördüncü derece trinomiallerin çarpanlara ayrılması

Polinomları gruplandırarak çarpanlara ayırma

Polinomları çarpanlara ayırmaya ilişkin çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Yorum bırakın Yanıtı iptal et