Polinom fonksiyonları

Bu makalede polinom fonksiyonları hakkında örneklerle desteklenen çok ayrıntılı bir açıklama bulacaksınız. Ayrıca sonunda sizlere sunacağımız alıştırmalar sayesinde polinom fonksiyonlarının günlük hayatta nasıl kullanıldığını görebileceksiniz.

Polinom fonksiyonu nedir?

Polinom fonksiyonları veya polinom fonksiyonları, bir polinoma eşdeğer bir cebirsel ifadeyle verilen fonksiyonlardır. Bu, ifadenin bir polinomun yapısını takip etmesi gerektiği anlamına gelir: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ , yapısına bağlı olarak işleyeceğimiz polinom fonksiyonunun türünü belirleyin. Bu fonksiyonların çok önemli bir başka özelliği de bilinmeyenlerin tüm üslerinin pozitif ve tamsayı olmasıdır.

Bir polinom fonksiyonunun parçaları

Bu işlevlere ilişkin üç önemli unsuru öne çıkarabiliriz:

• Polinom katsayıları: bilinmeyenlere eşlik eden sayılardır, örneğin aşağıdaki terimin 3’ü bir katsayıdır: 3x ² . Polinomdaki terim sayısı kadar katsayı olduğuna dikkat edilmelidir.
• Polinomun üsleri veya indeksleri: bunlar bilinmeyenlerin kuvvetleridir, örneğin aşağıdaki terimin 2’si bir üs: 3x ² . Daha önce de açıkladığımız gibi, bir polinom fonksiyonu durumunda bunlar her zaman pozitif ve tamsayı olacaktır.
• Polinomun derecesi: Bu değer, polinomu oluşturan tüm terimler arasında en yüksek derecenin üssüne eşdeğerdir. f(x) = 3x ² – 4x + 2 polinomu durumunda derece ikiye eşittir.

Bir fonksiyonun polinom olup olmadığını nasıl anlarsınız?

Bir polinom fonksiyonunu tanımlamak için az önce bahsettiğimiz özellikleri karşılayıp karşılamadığına bakmalıyız. Fonksiyonu tanımlayan ifadenin polinom yapısına sahip olup olmadığını kontrol ederek başlayacağız: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ . Daha sonra indislerin pozitif ve tam sayı olup olmadığını kontrol edeceğiz, bu basit adımlarla bir fonksiyonun polinom olup olmadığını belirleyebileceğiz.

Örneklerle Polinom Fonksiyon Türleri

Daha sonra, polinomun derecesine göre sınıflandırılan, mevcut polinom fonksiyonlarının farklı türlerini size göstereceğiz. Ek olarak, her tür için örnek bir grafiksel gösterim bulacaksınız. Bu polinom fonksiyon örnekleri sayesinde farklı kategoriler arasındaki farkları daha iyi görebileceksiniz.

sabit fonksiyonlar

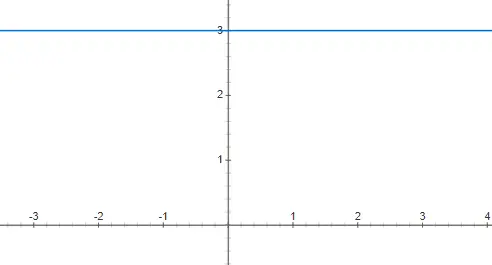
Sabit fonksiyonlar 0 dereceli bir polinomla eşdeğerdir; bu, x’in katsayısının 0 olduğu anlamına gelir. Bu tür fonksiyonların bağımsız x değişkeninin değerine bağlı olmamasının nedeni budur. Bu nedenle grafiksel gösterimi sonsuz olan yatay bir çizgidir. Aşağıda f(x) = 3’ün temsil ettiği örneği bulabilirsiniz:

birinci dereceden polinom fonksiyonları

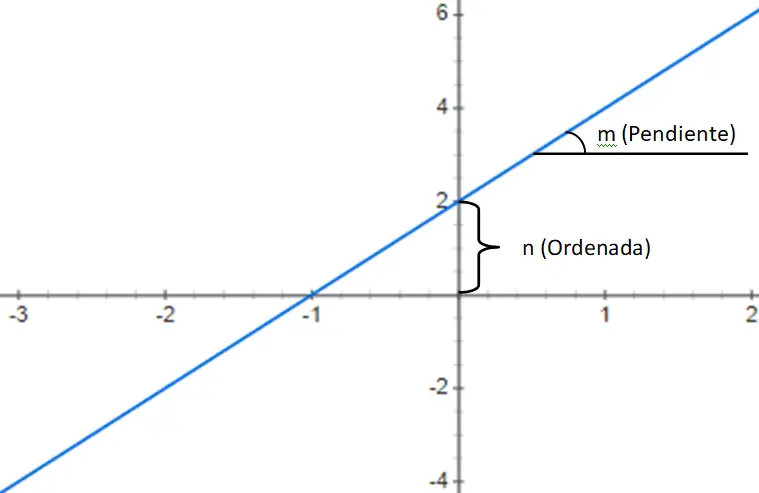
İkinci olarak, aşağıdaki yapıya sahip 1. derece polinom tarafından verilen birinci derece polinom fonksiyonlarını buluyoruz: f(x) = mx + n. Bu ifade, xy değişkenini bu çarpıma eklenen bir sabit (n) ile çarpan eğim (m) adı verilen bir sayıdan oluşur. Yani m ve n değerlerine dayanarak üç farklı fonksiyon tipini tanımlayabiliriz:

• Afin fonksiyonlar: Bu alt tip, n değerinin 0’dan farklı olmasıyla karakterize edilir, yani bilgisayarın değeri 0’dan farklıdır. Dolayısıyla bu fonksiyon türü, (0, 0) olarak da adlandırılan noktadan geçmez. köken. Ayrıca m < 0 ise fonksiyonun azalacağını, m > 0 ise fonksiyonun artacağını yorumlayın.
• Doğrusal fonksiyonlar: Bu fonksiyonların afin fonksiyonlardan tek farkı n = 0 olmasıdır, dolayısıyla bilgisayarları yoktur. Bu nedenle doğrusal fonksiyonların ifadesi f(x) = mx’e eşdeğerdir. Bu türün temsil edilmesi oldukça kolaydır, çünkü her zaman (0, 0) noktasından geçer ve grafiği zaten eğimden elde ederiz.
• Özdeşlik fonksiyonları: Bu son tip, an = 0 ve m = 1 olan doğrusal fonksiyonların bir alt grubudur. Bu, ifadenin f(x) = x olarak kaldığı anlamına gelir; burada grafiksel gösterim, f(x) = x ile 45°’lik bir açı oluşturan bir köşegendir. eksenlerden biri. Bu tür fonksiyon aynı zamanda başlangıç noktasından (0, 0) geçer.

Aşağıda birinci dereceden bir polinom fonksiyonunun, daha doğrusu f(x) = 3x + 2 afin fonksiyonunun bir örneğini bulacaksınız:

ikinci dereceden fonksiyonlar

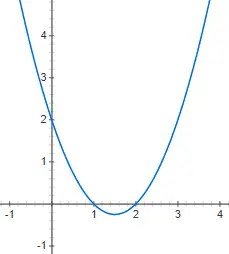
İkinci dereceden fonksiyonlar veya ikinci dereceden fonksiyonlar , şu yapıyı takip eden ikinci dereceden polinomlar kullanılarak ifade edilir: f(x) = ax ² + bx + c, burada a, 0’dan farklıdır. Bu durumda, grafik gösterimi çok daha karmaşıktır çünkü şu şekildedir: artık düz bir çizgi değil, dikey bir parabol . Aşağıda f(x) = 2x ² + 4x – 1 ikinci dereceden fonksiyonunun gösterimini bulabilirsiniz:

kübik fonksiyonlar

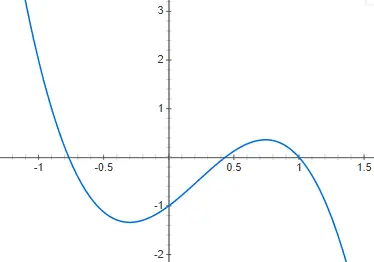
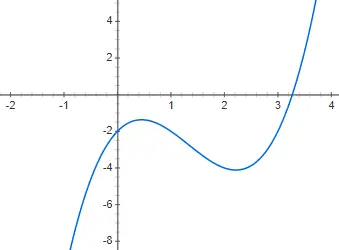
Üçüncü dereceden kübik fonksiyonlar veya fonksiyonlar üçüncü dereceden bir polinomla verilir: f(x) = ax ³ + bx ² + cx + d, 0’dan farklıdır. Bu stildeki bir fonksiyonun gösterimi, olduğundan daha da karmaşıktır. ikinci derecedendir, çünkü birçok farklı biçime sahip olabilir. Her ne kadar temel form veya en azından en yaygın olanı aşağıdaki örnekte size göstereceğimiz form olsa da, f(x) = 2x ³ – 4x ² + 2x – 2:

Polinom fonksiyonların özellikleri

Polinom fonksiyonların, onları diğer fonksiyonlardan ayıran bir dizi özelliği veya karakteristiği vardır ve bunları aşağıda mümkün olduğunca açık bir şekilde detaylandıracağız. Bu şekilde, bunun gibi işlevler gördüğünüzde bunları tanımlamanız çok kolay olacaktır:

• Bir polinom fonksiyonunun etki alanı tüm gerçek sayılara eşittir: Dom f = R veya Dom f = (-∞, ∞), dolayısıyla bunlar tüm gerçek sayılar kümesi üzerinde süreklidir.
• Y ekseni üzerindeki kesişme noktası (0, a ₀ )’a eşdeğerdir; ₀ bağımsız terimdir.
• X ekseni boyunca polinomun derecesine eşit veya bundan daha az sayıda keser.
• Polinom fonksiyonların asimptotları yoktur.
• Tüm terimlerin üssü tek ise grafik koordinat orijinine göre simetriktir, tüm terimlerin üssü çift ise OY eksenine göre simetriktir.
• Bu stildeki bir fonksiyonun dönüm noktalarının sayısı n – 2’ye eşit veya ondan küçüktür; burada n, derecedir.
• Bu stildeki bir fonksiyonun göreceli maksimum ve minimumlarının sayısı n – 1’e eşit veya ondan küçüktür; burada n, derecedir.

Bir polinom fonksiyonunu nasıl analiz edersiniz?

Bir polinom fonksiyonunu analiz etmek için, başka herhangi bir fonksiyonu analiz etmek için kullanacağımız prosedürün aynısını izlemeliyiz. Aşağıdaki listede incelenmesi veya ele alınması gereken farklı unsurları özetledik:

• Etki alanı ve aralık
• Yatay ve dikey eksenlerin kesişme noktaları
• Monotonluk (artan ve azalan, maksimum ve minimum)
• Eğrilik (birden büyük dereceli fonksiyonlarda)

Açıkçası, analizi başka bir seviyeye taşıyabilir ve diğer birçok unsuru inceleyebiliriz, ancak bu yeterli olacaktır. Çünkü bu unsurları bildiğinizden, fonksiyonun neye benzediğine dair net bir fikriniz olacak ve onu grafiksel olarak temsil edebileceksiniz.

Polinom fonksiyonları üzerine alıştırmalar

Daha sonra size, özellikle polinom fonksiyonları olmak üzere fonksiyonları temsil etme alıştırması yapabileceğiniz bir dizi alıştırma sunuyoruz. Bu şekilde, bu makalede açıklanan tüm kavramları birleştireceksiniz:

1. Egzersiz

Aşağıdaki birinci derece polinom fonksiyonu f(x) = x + 2’nin grafiğini çizin ve bunun ne tür olduğunu söyleyin:

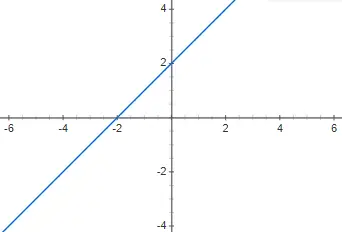
Birinci dereceden bir afin polinom fonksiyonudur çünkü 0’dan farklıdır ve m 0’dan farklıdır.

Alıştırma 2

Aşağıdaki ikinci dereceden polinom fonksiyonunun f(x) = x ² + x – 2 grafiğini çizin:

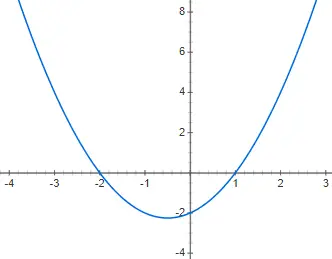
Alıştırma 3

Aşağıdaki üçüncü dereceden polinom fonksiyonunun f(x) = x ² + x – 2 grafiğini çizin: