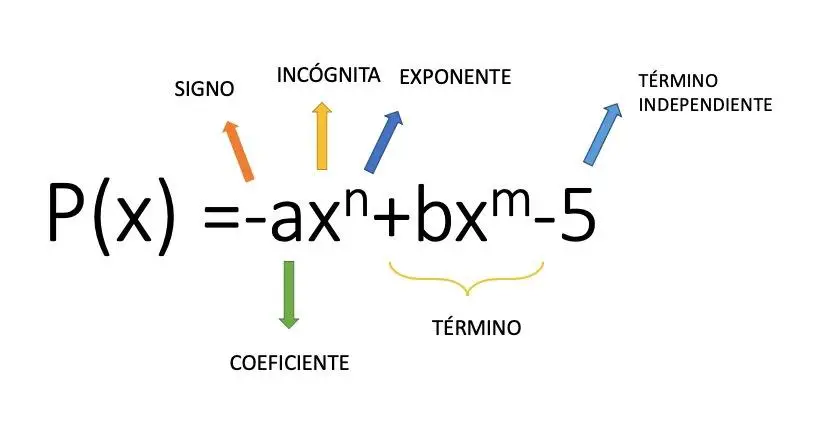
Bir monom, bir değişkeni bir üsle çarpan bir katsayı (sayısal değer) tarafından oluşturulan cebirsel bir ifadedir ; örneğin 4x² ifadesi bir monomdur. Bu matematiksel kavramdan, çeşitli tek terimlilerin toplama ve çıkarmalarından oluşan bir dizi olan polinoma ulaşıyoruz. Yukarıdaki resimde birkaç tek terimliden oluşan bir polinomun yapısının bir örneğini görebilirsiniz.
polinom türleri
Belirli bir tek terimlinin üssü aracılığıyla polinomları farklı türlere ayırabiliriz. Bu ifadeleri birinci derece polinom, ikinci derece polinom, üçüncü derece polinom vb. gibi kategorilere ayırabiliriz. Temel olarak, en büyük üsse sahip olan ve polinomun derecesi olacak tek terimliyi tanımlamanız gerekir. Ve bunu öğrendikten sonra, onu az önce bahsettiğimiz türlerden birine göre sınıflandırabilirsiniz.
Çeşitli değişkenlerin polinomu
Ek olarak, polinomları oluşturan tek terimlilerin sayısına göre düzenlemenin başka bir yolu da vardır. Örneğin, eğer bir binomumuz varsa, bu iki terimli bir polinoma sahip olmaya eşdeğer olacaktır; eğer bir trinomiye sahipsek, bu, üç terimli bir polinoma sahip olmaya eşdeğer olacaktır, vb. Polinomları kataloglamanın tüm bu yollarının sonsuz sayıda alt kategorisi vardır. Çünkü bu ifadeler istediğimiz tek terimlilerden oluşabileceği gibi, herhangi bir dereceye de sahip olabilir.
Polinomların özellikleri ve özellikleri
- Bir polinomun mutlak derecesi: Önceki bölümde bağıl derecenin tanımını tartışmıştık. Ancak birden fazla değişkenin oluşturduğu polinomlar söz konusu olduğunda, bu monomiyalin tüm değişkenlerinin üslerinin maksimum toplamına eşdeğer olan mutlak dereceye sahip oluruz. Örneğin 5x²y³ tek terimlisinde mutlak derece 2 + 3 = 5’e eşittir.
- Sıralı polinom: Bir değişkene göre sıralı bir polinomu, o değişkenin üsleri artan veya azalan sırada düzenlendiğinde tanımlarız. Örneğin bu polinomu P(x) = 3x + 4x³ – x² bulursak bu durumda sıralanmayacaktır. O halde bunu düzeltirsek şu sonucu elde ederiz: P(x) = 4x³ – x² + 3x.
- Tam polinom: Mümkün olan tüm üsleri (en yüksek dereceden bağımsız terime kadar) içeren tek terimli bir polinom bulduğumuzda, bunun tam bir polinom olduğunu söyleriz. Örneğin aşağıdaki ifade: P(x) = 3 x² + 2x – 4 bu türdendir çünkü 2 ile 0 arasında eksik bir üs yoktur.
- Homojen polinom: Her monomunun mutlak derecesi eşit olan polinomdur. Değişkenler üs olarak farklı değerlere sahip olabilir ancak tüm monomlardaki değişkenlerin üslerinin toplamının mutlaka aynı olması gerekir. Örneğin: P(x) = x²y³z + 3 x 4 yz, iki toplam altı 2 + 3 + 1 = 4 + 1 + 1 = 6 verir.
- Özdeş polinomlar: Aynı terimlerin katsayılarını paylaşan iki veya daha fazla polinom bulduğumuzda, bunların özdeş polinomlar olduğunu söyleyeceğiz. Aşağıda iki polinom arasındaki örneği görebilirsiniz: P(x) = 2x + 27 ve Q(x) = 5 (x + 3) – 3 (x – 4), her üssün katsayılarını paylaştıkları için aynı olacaklar : 2x = 5x – 3x ve 27 = 15 + 12.
- Sıfır polinom: Bu polinomun yalnızca sıfır katsayıları vardır (sıfıra eşit), dolayısıyla polinomun toplam değeri de sıfır olacaktır. P(x) = 0x³ + 0x² – 0x – 0 polinomu bu tür polinomun açık bir örneğidir, ancak Q(x) = 0 ile karıştırılmamalıdır, çünkü bu durumda bir denklem oluşturursunuz ve bu Q(x)’in tüm katsayılarının 0 olduğu anlamına gelmez.
Bir polinomun sayısal değeri
Bir polinomun sayısal değeri, bu ifadenin değişkenini bir sayının yerine koyarak elde edeceğimiz sonuçtur. Bu polinomu sanki birleşik bir işlemmiş gibi çözmemiz gerekiyor. Daha sonra bunun gibi bir ifadenin sayısal değerini elde etmek için kullanabileceğiniz üç yöntemi açıklayacağız.
- Doğrudan değiştirme: Polinomun değişkenlerinin her birine karşılık gelen değerler bize doğrudan verildiğinde, bu değişkenleri bu sayıların yerine koyarız. Bu şekilde P(x) = 2x² – x + 4 polinomumuz varsa ve x = 3 olduğu söylenirse polinomun sayısal değeri 2 · 3² – 3 + 4 = 19 olacaktır.
- Değişken çözünürlük: Değişkenin değerini doğrudan bize vermedikleri ancak eşdeğerlik verdiklerinde bu durumu uygulayacağız. Örneğin, P(2) Eğer P(x – 1) = x³ – 2x + 1 doğruysa, o zaman önce 2 = x – 1 denklemini çözeceğiz ve x = 3 elde edeceğiz. Son olarak, 3’ü yerine koymamız gerekecek. x, öyle ki 3³ – 2 · 3 + 1 = 22.
- Değişken değişimi: P(x) = 4x – 2 polinomumuz olduğunda ve P(x + 2) için bu değeri bilmek istediğimizde. Daha sonra ifadedeki tüm x’leri a(x+2) olarak değiştirmemiz gerekiyor. Bununla birlikte, bu son çözülmüş örneğin neye benzeyeceğine bakalım: P (x + 2) = 4 (x + 2) – 2.
Polinomlarla işlemler
Aşağıda dört temel aritmetik işlemin polinomlarla nasıl çözüleceğini, her zamanişlem hiyerarşisini takip ederek açıklayacağız. Her bölümde, her durumda nasıl ilerleyeceğinizi bilmenizi sağlayacak küçük bir teori ve bazı pratik örnekler bulacaksınız.
polinomların eklenmesi
Polinomları eklemek için bunların yalnızca benzer terimlerle gruplandırılabileceği gerçeğini hesaba katmalıyız; dolayısıyla P(x) = 3x³ – x² + 2x – 4 ve Q(x) = 2x² + 3x – 2 polinomlarımız varsa. P(x) + Q(x) yapmak için aynı üssün eşlik ettiği iki polinomun katsayılarını toplayacağız: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. Özetle her benzer terimin katsayılarını gruplayıp topladığımızı ve sonunda tüm terimleri tek bir polinomda ifade ettiğimizi söyleyebiliriz. .
polinomların çıkarılması
Polinomların çıkarılması toplama işlemiyle aynı şekilde çözülür, tek fark elbette semboldür. Daha sonra benzer terimleri bir araya toplayıp çıkarıyoruz ve hepsini tek bir ifadeye dönüştürüyoruz. Aşağıda size bir örnek kullanarak göstereceğiz: P(x) = 5x³ – 2x² + x – 3 ve Q(x) = 3x² + 5x + 4, ardından P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.
polinom çarpımı
Bu tür çarpma işlemlerini çözerken işler biraz karmaşıklaşabilir, ancak size anlatacağımız tüm adımları izlerseniz sorun yaşamazsınız. Bu matematiksel işlemde tüm tek terimliler diğerleriyle birlikte çalışacaktır; bu, yalnızca benzer terimleri çarpmayacağımız anlamına gelir. Ayrıca katsayıların yanı sıra üsler de değişecek . Bu örnekle her şeyi daha iyi anlayacaksınız: P(x) = 2x² + 3x – 1 ve Q(x) = 2x + 3:
P(x) Q(x) = ( 2x² + 3x –1 ) · ( 2 kere + 3 ) = 2x² · 2 kere + 2x² · 3 + 3x · 2 kere + 3x · 3 + (-1 ) · 2 kere + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3
Temel olarak, bir polinomun her teriminin katsayılarını ikinci terimin tüm katsayılarıyla çarparız, sonra a n · a m = a n+m’nin kuvvet özelliğini uygularız.
polinomların bölünmesi
Son olarak, yalnızca polinomların bölünmesinin nasıl çözüleceğini açıklamamız gerekiyor, temel olarak bölmenin dağılma özelliğini uygulamamız gerekiyor: (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷ d). Ayrıca aşağıdaki üstel alma özelliğini n ÷ a m = a nm’ye de uygulayacağız. Şimdi bunu basit bir örnekle göreceğiz: P(x) = 3x³ – 6x² + 9x ve Q(x) = 3x.
P(x) ÷ Q(x) = ( 3x³ – 6x² +9x ) ÷ 3x = ( 3x³ ÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = x² – 2x + 3
Artık tüm bu işlemleri polinomlarla nasıl çözeceğinizi görmeyi bitirdiğinize göre, bunu pratikte nasıl uygulayacağınızı bildiğinizi umuyoruz. Ancak durumun böyle olmadığını düşünüyorsanız ve biraz pratik yapmaya devam etmek istiyorsanız o zaman bu sayfadaki bazı çözümlü alıştırmalara göz atmanızı öneririz. Bunlar, tüm bu matematiksel kavramları içselleştirmenizi tamamlamanıza yardımcı olacaktır.
Polinomları çarpanlara ayırma
Polinomları çarpanlara ayırmak için bu son bağlantıdaki makalede açıklandığı gibi manuel olarak veyaRuffini hesap makinesi kullanarak yapabilirsiniz. Hızlı bir şekilde yapmak istiyorsanız bunu ikinci seçenekle yapmanızı öneririz, ancak yalnızca nasıl çarpanlara ayrılacağını öğreniyorsanız, manuel olarak pratik yapmanız daha iyi olur. Bunu yapmanın yolu durumunuza göre seçilmelidir.
Polinomları bilimsel hesap makinesiyle çözün
Bugün piyasada birçok farklı bilimsel hesap makinesi var. Ancak polinomları çözebilecek ucuz bir hesap makinesi arıyorsanız Casio FX-991SPX II’yi öneriyoruz. Kullanımı kolay, çok güçlü ve işlevseldir, bu da onu her ortaokul ve lise matematik öğrencisi için mükemmel kılar. Aşağıda bu tarzdaki matematiksel ifadelerin bu veya buna benzer bir Casio modeli kullanılarak nasıl çözüldüğünü kısaca açıklayacağız.
Önce değişkenlerin sayısal değerini girip yazmalı, ardından “STO” + değişkenin harfine basmalısınız, örneğin x. Yani tüm değişkenler tanımlandığında, polinom ifadesini tüm değişkenlerde ve tüm sayılarda olduğu gibi yazmanız yeterlidir. Ve son olarak eşit tuşuna basmalısınız, böylece polinomun sayısal değerine eşdeğer sonuç elde edeceksiniz.