Pi sayısı, bir dairenin çevresi ile çapı arasındaki ilişkiyi temsil edenmatematiksel bir sabittir . Bu irrasyonel bir sayı. Başka bir deyişle tam bir kesir değildir . Bu nedenle sonlu bir ondalık sayı olarak gösterilemez. Pi’nin değeri yaklaşık 3,14159’dur ve Yunanca π harfiyle temsil edilir.
Pi matematikte önemli bir sayıdır. Bu nedenle çeşitli alanlarda birçok uygulaması bulunmaktadır. Örneğin geometride alanı hesaplamak için kullanılır. Ayrıca dairelerin ve diğer dairesel şekillerin çevresi. Öte yandan trigonometride yayların açıları ve uzunlukları hesaplanır. Son olarak mühendislik ve fizikte hacim ve kapasite gibi büyüklüklerin hesaplanması.
Pi Günü her yıl 14 Mart’ta kutlanıyor çünkü tarih Pi’nin (3.14) değerine yakın. Bu tarih, Pi’nin matematikteki rolünü anmak ve bu temel sabite olan ilgiyi artırmak için kutlanıyor.
Pi sayısını kim keşfetti?
Pi sayısı Antik Çağ’dan beri bilinmektedir ve onu tam olarak tanımlayan kişi Yunan matematikçi Arşimet’tir (M.Ö. 287-212). Aslında bunu geometrik şekillerin alanını ve hacmini hesaplamak için kullandı.
18. yüzyılda İsviçreli matematikçi Johann Lambert Pi’nin irrasyonel bir sayı olduğunu kanıtladı. Daha sonra 19. yüzyılda Alman matematikçi Ferdinand von Lindemann Pi’nin aşkın bir sayı olduğunu açıkladı. Yani rasyonel katsayılı bir polinom denkleminin tam çözümü olarak ifade edilemez.
Tarih boyunca farklı matematikçiler Pi sayısının anlaşılmasına katkıda bulunmuşlar ve onu daha hassas bir şekilde hesaplamak için teknikler geliştirmişlerdir. Bugün Pi dünyadaki en önemli ve en iyi bilinen matematiksel sabitlerden biri olmaya devam ediyor ve matematikte bir çalışma konusu olmaya devam ediyor.
Pi sayısı neden sonsuzdur?
Pi’nin değeri yaklaşık olarak 3,14159’dur ancak gerçekte virgülden sonra sonsuza kadar devam eden bir sayıdır. Bu, Pi’nin sonsuz bir sayı olduğu ve ondalık sayılarla tam olarak temsil edilemeyeceği anlamına gelir.
Pi’nin değeri sonsuz olmasına rağmen pratikte Pi’nin yaklaşık değerleri büyük bir hassasiyetle hesaplanabilmektedir. Şimdiye kadar Pi’nin milyonlarca basamağı hesaplanmış ve ondalık basamaklarında düzenli desenlerin olmadığı gösterilmiştir. Gerçi bu süper bilgisayarlar aracılığıyla yapıldı çünkü o kadar çok sayıyı hesaplayamıyoruz.
Pi sayısının yaklaşık değerini hesaplamak için hangi yöntemler mevcuttur?
Pi değerini hesaplamanın birkaç pratik yöntemi vardır.Daha sonra matematikçilerin en çok kullandığı üç yöntemi adım adım açıklayacağız.
1. Arşimed’in yöntemi
Yunan matematikçi Arşimed, Pi’nin yaklaşık değerini hesaplamak için geometrik bir yöntem kullandı. Bu yöntemi kullanmak için aşağıdaki adımları izleyin:
1. Bir daire çizin ve dairenin merkezinden geçen bir çizgi çizin ve bunu aşağıda gösterildiği gibi iki zıt noktada kesiştirin:
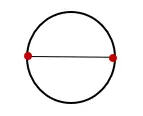
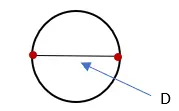
2. Çemberi kesen çizginin uzunluğunu ölçün ve onu “D” olarak etiketleyin. Bu ölçüm dairenin çapıdır.
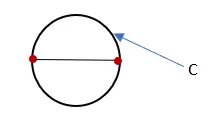
3. Daireyi oluşturan çizginin uzunluğunu ölçün ve onu “C” olarak etiketleyin. Bu ölçüm dairenin çevresidir.
4. Dairenin çevresini (C) dairenin çapına (D) bölün. Sonuç Pi’nin yaklaşık değeridir.
Örneğin: eğer dairenin çapı 6 ve çevresi 18 ise Pi’nin yaklaşık değeri 18 ÷ 6 = 3 olur. Açıkçası bu örnek çok basit, ancak bunu gerçek bir çevrenin değerleriyle yaparsanız yöntemin doğru çalıştığını göreceksiniz.
Aslında bunu denemenizi öneririz: Bir bardağın veya dairesel şekle sahip bir şeyin ölçülerini alın ve işinize yarayıp yaramayacağını görün.
2. Monte Carlo yöntemi
Monte Carlo yöntemi Pi’nin yaklaşık değerlerini hesaplamak için kullanılan olasılıksal bir yöntemdir.Bunu yapmak için bir düzlem üzerinde rastgele çok sayıda nokta oluşturulur ve bir kare içine yazılan bir dairenin içine sığan noktaların sayısı sayılır. İşlem şu şekilde uygulanır:
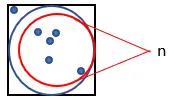
1. Kenarı 1 olan karenin içine aşağıda gösterildiği gibi bir daire çizin:

2. Karede rastgele çok sayıda nokta oluşturun.
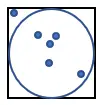
3. Çembere sığan noktaları sayın. Bu miktara “n” diyelim.
4. Oluşturulan toplam puan sayısını sayın. Bu miktarı “m” olarak adlandırın.
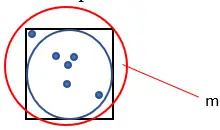
5. Aşağıdaki formülü kullanarak Pi’nin yaklaşık değerini hesaplayın: Pi = (4 · n) ÷ m.
Örneğin, 380 nokta oluşturulduysa ve 300 nokta daireye sığdıysa Pi’nin yaklaşık değeri (4 · 300) ÷ 380 = 3,16 olur. Bu değer, Pi’nin ilk iki ondalık basamağına çok benzer, ancak tıpkı önceki yöntem gibi, gerçek ölçümleri kullanmak size daha da kesin bir değer verecektir.
3. Yineleme yöntemi
İterasyon yöntemi, Pi’nin yaklaşık değerlerini hesaplamak için kullanılan matematiksel bir yöntemdir. Bu yöntem, Pi’nin değerini ima eden bir formül kullanır ve hesaplamanın doğruluğunu artırmak için yinelemeli olarak uygulanır. Bu yöntemi kullanmanın adımları şunlardır:
- Pi için bir başlangıç değeri seçin. Örneğin 3 değerini seçebilirsiniz.
- Yeni bir yaklaşık değer hesaplamak için Pi değerini içeren bir formül kullanın. Örneğin aşağıdaki formülü kullanabilirsiniz: Pi = (Pi + (4 ÷ Pi)) ÷ 2
- Yeni yaklaşık değeri eski değerle karşılaştırın. İkisi arasındaki fark yeterince küçükse doğru sonuca ulaştınız demektir. Fark hala önemliyse yeni değeri Pi’ye atayın ve işlemi 2. adımdan itibaren tekrarlayın.
Örneğin, Pi’nin başlangıç değeri 3 ise, yeni yaklaşık değer (3 + (4 ÷ 3)) ÷ 2 = 2,66666666 olacaktır. Ancak ikisi arasındaki fark çok küçük olmadığı için doğru değeri bulmadan önce işlemi her zaman birkaç kez tekrarlayabilirsiniz.
Pi sayısının uygulamaları nelerdir?
Pi matematikte önemli bir sayıdır ve çeşitli alanlarda birçok uygulaması vardır. Pi’nin en önemli uygulamaları arasında aşağıdakilere sahibiz:
Geometri
Pi geometride dairelerin ve diğer dairesel şekillerin alanını ve çevresini hesaplamak için kullanılır:
- Daireler : Dairelerin alanını ve çevresini hesaplayın.
- Küreler : Kürelerin alanını ve hacmini belirler.
- Silindirler : Silindirlerin yüzey alanı ve hacminin hesaplanması.
- Koniler – Konilerin yüzey alanını ve hacmini hesaplamak için kullanılır.
Trigonometri
Trigonometride açıları ve yay uzunluklarını hesaplamak için kullanışlıdır. Uygulamalarından bazıları şunlardır:
- Açılar : açıların ve yay uzunluklarının hesaplanması.
- Trigonometrik Fonksiyonlar – Belirli açılar için trigonometrik fonksiyonların değerini hesaplamak için kullanılır.
- Dairesel trigonometri : 360 derecelik açılar için trigonometrik fonksiyonların değerlerini hesaplamak için.
Mühendislik
Mühendislikte Pi, hacim ve kapasite gibi büyüklüklerin hesaplanmasında kullanılır. Uygulamalarından bazıları şunlardır:
- Elektronik : direnç ve kapasitans gibi büyüklükleri hesaplar.
- Elektrik : Güç ve elektrik enerjisi gibi büyüklüklerin hesaplanmasında kullanılır.
- İnşaat mühendisliği : Yapıların ve inşaat elemanlarının yüzey alanı ve hacmi gibi miktarları hesaplar.
Fiziksel
Pi (π) sayısı fizikte birçok uygulamaya sahip bir matematiksel sabittir. Pi’nin fizikte kullanımına ilişkin bazı örnekler:
- Dalgalar – Dalgaların frekansını ve dalga boyunu hesaplamak için kullanılır.
- Mekanik : Mekanikte dönen sistemlerde iş ve enerjinin hesaplanmasında faydalıdır.
- Elektromanyetizma : Elektromanyetizmada, bir kapasitörde depolanan enerjiyi ve bir sarımdaki endüktansı hesaplamak için kullanılabilir.
- Kozmoloji Kozmolojide Pi, uzay-zamanın eğriliğini ve evrenin genişlemesini hesaplamak için kullanılır.
Pi sayısının gerçek hayatta hangi uygulamaları var?
Pi’nin günlük yaşamda nasıl kullanıldığına dair bazı örnekler:
- Geometri : Dairesel bir matın alanını tanımlamak veya dairesel bir masanın çevresini kaplamak için gereken şerit ölçüsünün uzunluğunu ölçmek için.
- Pişirme – bir tencereyi doldurmak için ne kadar su veya sıvı gerektiğinin veya dairesel bir kaba kaç malzemenin sığacağının belirlenmesi.
- Astronomi : Gezegenler ve yıldızlar arasındaki mesafeyi, gezegenlerin yörüngelerini ve gök cisimlerinin gökyüzündeki konumunu bilir.
- Bahçecilik : Dairesel bir saksıyı doldurmak için gereken toprak veya toprak miktarını öğrenin veya dairesel bir bahçedeki bir bitkiyi sulamak için gereken su miktarını hesaplayın.