Paralel çizgiler - Mathority

Burada paralel çizgilerle ilgili her şeyi bulacaksınız: ne anlama geldikleri, iki doğrunun paralel olup olmadığının nasıl belirleneceği, özellikleri vb. Ayrıca paralel doğrularla ilgili çeşitli örnekler ve çözülmüş alıştırmalar görebileceksiniz.

Paralel çizgiler nedir?

Paralel çizgiler hiçbir zaman kesişmeyen, yani yörüngeleri sonsuza kadar uzansa bile birbirlerine asla değmeyen çizgilerdir. Bu nedenle iki paralel doğrunun noktaları birbirine her zaman aynı uzaklıkta olur ve üstelik iki paralel doğrunun hiçbir ortak noktası yoktur.

Örneğin aşağıdaki iki çizgi paraleldir:

Genellikle iki doğrunun 2 dikey çubukla paralel olduğunu belirtiriz || Çizgilerin arasında

Öte yandan iki paralel doğru hiçbir zaman kesişmese de analitik geometride yönleri aynı olduğundan 0° açı oluşturduğunu söyleriz.

İki doğru ne zaman paralel olur?

Paralel doğruların tanımını gördükten sonra iki paralel doğrunun nasıl bulunacağını göreceğiz. Açıkçası bir yol, çizgilerin grafiğini çizmek ve grafikte kesişip kesişmediklerini görmek olabilir, ancak daha basit ve kullanımı daha kolay yöntemler de vardır.

İki doğrunun eğimleriyle paralelliğini belirleyin

İki doğrunun paralel olup olmadığını her bir doğrunun eğimine bakarak anlayabilirsiniz. Bir çizginin eğiminin parametre olduğunu unutmayın

$m$

açık denklemden ve çizginin nokta-eğim denkleminden:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Bununla birlikte, bir çizginin eğimini belirlemenin birkaç yolu vardır, bu nedenle nasıl hesaplanacağını öğrenmek için çizginin eğimi formülüne göz atmanızı öneririz. Ek olarak bağlantılı sayfada bir doğrunun eğiminin neyi temsil ettiğine ve bunun bir doğru için neden bu kadar önemli olduğuna dair bir açıklama da bulacaksınız.

Böylece, düzlemde, aynı eğime (katsayı m) ve orijinde farklı ordinatlara (katsayı n) sahip olan iki doğru paraleldir .

Örneğin aşağıdaki iki çizgi paraleldir:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

Bunlar iki paralel doğrudur çünkü her ikisinin de eğimi aynıdır, üstelik bağımsız terimleri de farklıdır.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

Şunu belirtmek gerekir ki, eğer iki doğru aynı eğime sahipse ve orijinde aynı anda aynı bilgisayara sahip olsaydı, bunların tamamen aynı olacağı için aynı doğrular olacağı unutulmamalıdır.

Örtülü denklemden iki doğrunun paralelliğini bulun

Doğrunun örtülü (veya genel) denkleminin şöyle olduğunu unutmayın:

$Ax+By+C=0$

Dolayısıyla iki doğrunun A ve B katsayıları birbiriyle orantılı ancak C katsayısıyla orantılı değilse bu, doğruların paralel olduğu anlamına gelir.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

Genel (veya örtülü) denklem formunda ifade edilen iki paralel çizgi aşağıda verilmiştir:

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

Paraleldirler çünkü değişkenin önündeki sayılar

$x$

değişkenin önündeki sayılarla orantılıdır

$y$

, ancak bağımsız terimlerle değil.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

Daha önce olduğu gibi, eğer iki örtülü doğrunun tüm katsayıları (A, B ve C) orantılı olsaydı, bu, iki doğrunun çakıştığı, başka bir deyişle eşit oldukları anlamına gelirdi.

Paralel çizgilerin özellikleri

Paralel çizgilerin özellikleri aşağıdaki gibidir:

Simetrik özellik : Bir doğru diğerine paralel ise bu doğru da birinciye paraleldir. Bu özelliğe dik çizgiler de sahiptir.

$r \parallel s \ \longrightarrow \ s \parallel r$

Geçiş özelliği : Bir doğru başka bir doğruya paralel ise ve bu ikinci doğru da üçüncü doğruya paralel ise, birinci doğru da üçüncü doğruya paraleldir.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

İki paralel doğrunun yön vektörlerinin (bir çizginin yönünü gösteren vektör) skaler çarpımı , modüllerinin çarpımına eşittir.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

Ayrıca iki paralel doğrunun yön vektörleri orantılı olduğundan her zaman birbirine doğrusal olarak bağımlıdır.

Bu koşul doğruların paralel olması için gereklidir ancak yeterli değildir veya başka bir deyişle iki paralel doğrunun orantısal yön vektörlerine sahip olması gerekir ancak iki doğrunun orantısal yön vektörlerine sahip olması doğrudan paralel oldukları anlamına gelmez. Çakışmalı doğruların aynı zamanda orantılı yön vektörleri de vardır.

Apsis eksenine (X ekseni) paralel çizgiler yataydır ve her zaman forma sahiptir
$y=k.$

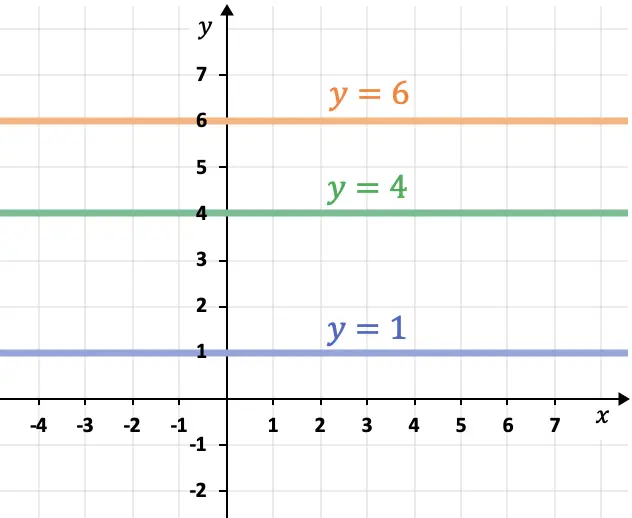
Bilgisayar eksenine (Y ekseni) paralel çizgiler dikeydir ve her zaman ifadeyi takip eder
$x=k.$

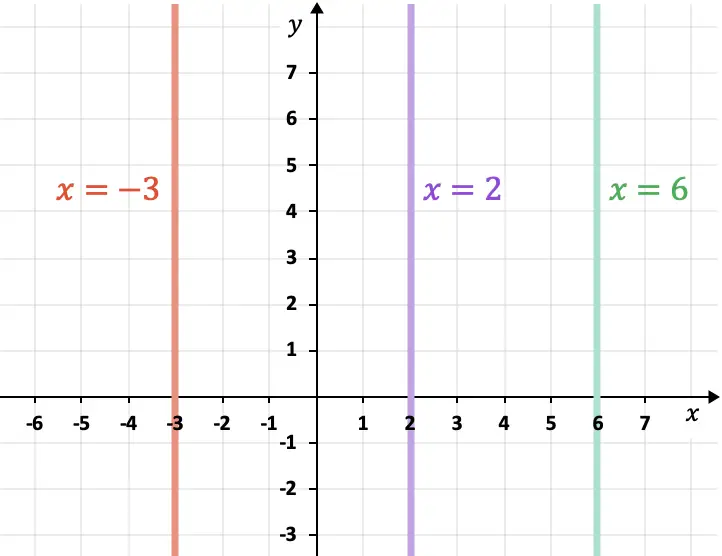
Düzlemdeki iki paralel çizgi arasındaki mesafe nasıl hesaplanır

Düzlemdeki (R2’deki) iki paralel çizgi arasındaki mesafeyi bulmak için, iki çizgiden birinin üzerinde bir nokta alın ve bu noktadan diğer doğruya olan mesafeyi hesaplamanız yeterlidir.

Bunu bu şekilde yapabiliriz çünkü iki paralel çizgi birbirinden her zaman aynı uzaklıkta olur.

Öte yandan formülü kullanırken 0 birimlik bir mesafe elde edersek bu, çizgilerin bir noktada birbirine değdiği ve dolayısıyla çizgilerin paralel olmadığı, kesiştiği, çakıştığı veya dik olduğu anlamına gelir. İsterseniz bu tip hatlar arasındaki farkları sitemizden inceleyebilirsiniz.

Bunun nasıl yapıldığını görebilmeniz için örnek olarak aşağıdaki iki paralel çizgi arasındaki mesafeyi belirleyeceğiz:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Yapmamız gereken ilk şey çizgilerden birinde (istediğiniz çizgide) bir nokta almak. Bu durumda doğru üzerinde bir nokta hesaplayacağız.

$s.$

Bunu yapmak için değişkenlerden birine değer vermeliyiz, örneğin yapacağız

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Ve şimdi diğer değişkeni temizliyoruz (

$y$

) Bu noktada değerinin ne kadar olduğunu bilmek için elde edilen denklemin:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Bu nedenle doğrudan elde edilen nokta

$s$

Doğu:

$P(0,-2)$

Ve bir çizgi üzerinde zaten bir noktamız olduğunda, bir noktadan bir çizgiye olan mesafe formülünü kullanarak o noktadan diğer çizgiye olan mesafeyi hesaplarız:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

Dolayısıyla iki paralel çizgi arasındaki mesafe 0,45 birime eşittir .

Paralel Doğrular Çözülmüş Sorunlar

1. Egzersiz

Aşağıdaki doğrulardan hangisi paraleldir?

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

Çözüme bakın

İki doğru aynı eğime (ve farklı kesişme noktalarına) sahipse paraleldir. Böylece her doğrunun eğimi şu şekilde olur:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

Yani sadece doğrular paraleldir

$r$

$q,$

çünkü eğimleri eşit olan tek canlı onlar.

Alıştırma 2

Doğruya paralel doğrunun açık denklemini bulun

$r$

ve bu noktada ne olur?

$P(0,2).$

düz olmak

$r:$

$r: \; y=3x-1$

Çözüme bakın

Böylece çizgi çizgiye paralel olur

$r,$

her ikisinin de aynı eğime sahip olması gerekir. ve çizginin eğimi

$r$

$m = 3$

Bu nedenle bulmamız gereken doğrunun açık denklemi şöyle olacaktır:

$y=3x+n$

Doğrunun eğimini bildiğimizde, doğruya ait olan noktayı doğrunun denkleminde yerine koyarak kesişme noktasını hesaplayabiliriz:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

Dolayısıyla doğrunun açık denklemi şöyledir:

$\bm{y=3x+2}$

Alıştırma 3

Bilinmeyenlerin değerini hesaplayın

$a$

$b$

aşağıdaki iki çizgi paralel olacak şekilde:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

çözümü gör

Çizgiler genel (veya örtülü) denklem formunda açıklanmaktadır. Dolayısıyla iki doğrunun paralel olabilmesi için A ve B katsayılarının orantılı olması yani aşağıdaki denklemin gerçekleşmesi gerekir:

$\cfrac{2}{1} = \cfrac{-4}{a}$