Parabol (matematik): tanımı, denklemi, elemanları, örnekleri,…

Bu sayfada parabol hakkında her şeyi bulacaksınız: ne olduğunu, neyi temsil ettiğini, elemanlarını (odak, doğrultman, köşe vb.), denklemini (parabolün farklı denklem türleriyle birlikte), örnekleri, çözülmüş alıştırmaları, özellikleri, uygulamaları,…

Bir benzetme nedir?

Parabol çok farklı anlamlara sahip bir kavramdır ancak matematiksel tanımı şu şekildedir:

Matematikte parabol, düzlem üzerinde sabit bir noktadan (odak adı verilen) ve sabit bir çizgiden (doğrultman adı verilen) eşit uzaklıkta olan noktaların yeridir.

Bu nedenle, bir paraboldeki herhangi bir nokta, odağına ve doğrultusuna aynı uzaklıkta olur.

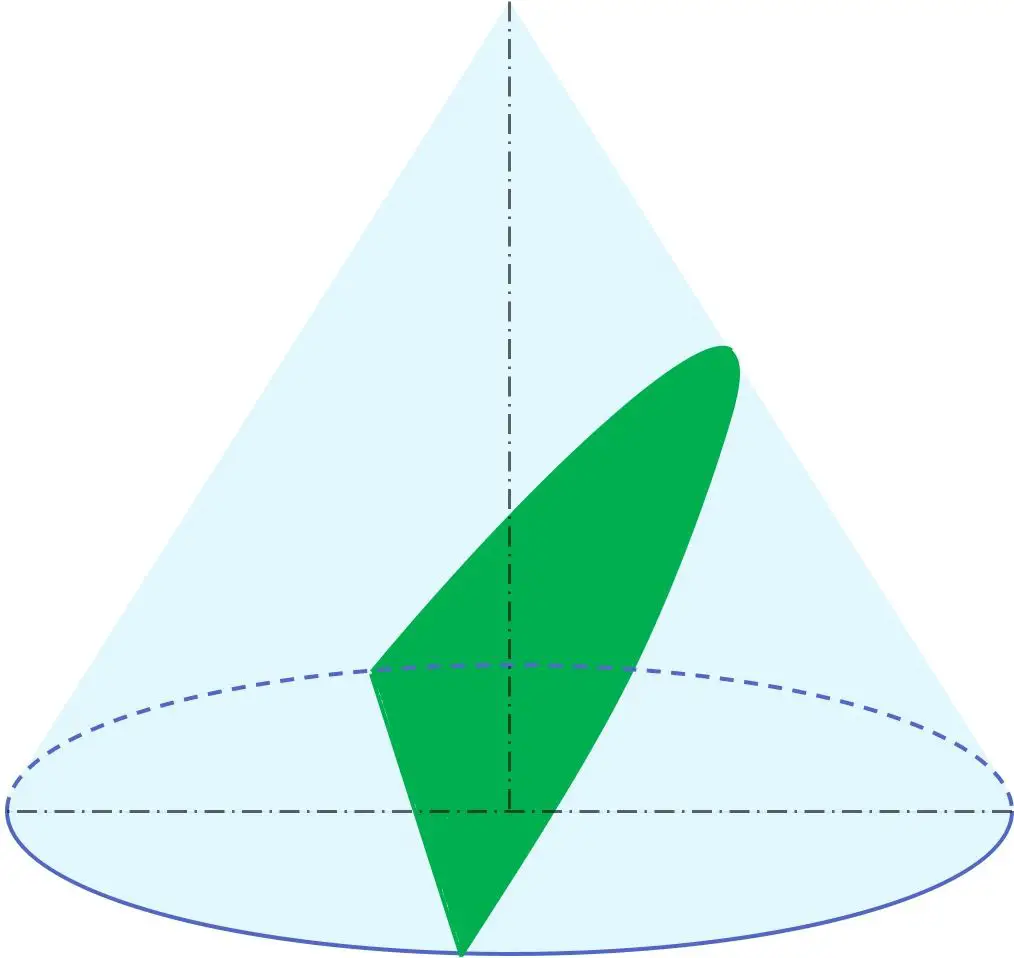
Ayrıca geometride parabol, çevre, elips ve hiperbol ile birlikte konik bölümlerden biridir. Başka bir deyişle bir koniden bir parabol elde edilebilir.

Özellikle parabol, bir koninin, dönme eksenine göre, koninin üretecinin açısına eşdeğer bir eğim açısına sahip bir düzlem tarafından kesitinden kaynaklanır. Bu nedenle parabolün bulunduğu düzlem koninin üretecine paraleldir.

Bir parabolün elemanları

Bir parabolün özellikleri aşağıdaki unsurlara bağlıdır:

Odak (F) : parabolün içinde sabit bir noktadır. Parabolün herhangi bir noktasından odağa olan mesafe, aynı noktadan parabolün doğrultusuna olan mesafeye eşittir.
Directrix (D) : Parabolün dışında sabit bir çizgidir. Parabolün bir noktası, doğrultmana ve parabolün odağına aynı mesafededir.
Parametre (p) : Odaktan yönetmene olan mesafedir.
Yarıçap vektörü (R) : Parabolün bir noktasını odağa birleştiren segmenttir. Değeri, noktadan direktriye olan mesafeyle çakışır.
Eksen (E) : Odaktan geçen doğrultmana dik olan ve parabolün simetri ekseni olan çizgidir, aşağıdaki grafikte bilgisayar eksenine (Y ekseni) karşılık gelir. Odak ekseni olarak da adlandırılır.
Tepe Noktası (V) : Parabol ile ekseni arasındaki kesişme noktasıdır.
Odak uzaklığı : Odak ile tepe noktası arasındaki veya direktrix ile tepe noktası arasındaki mesafedir. Değeri her zaman eşittir
$\displaystyle \frac{p}{2}.$

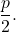
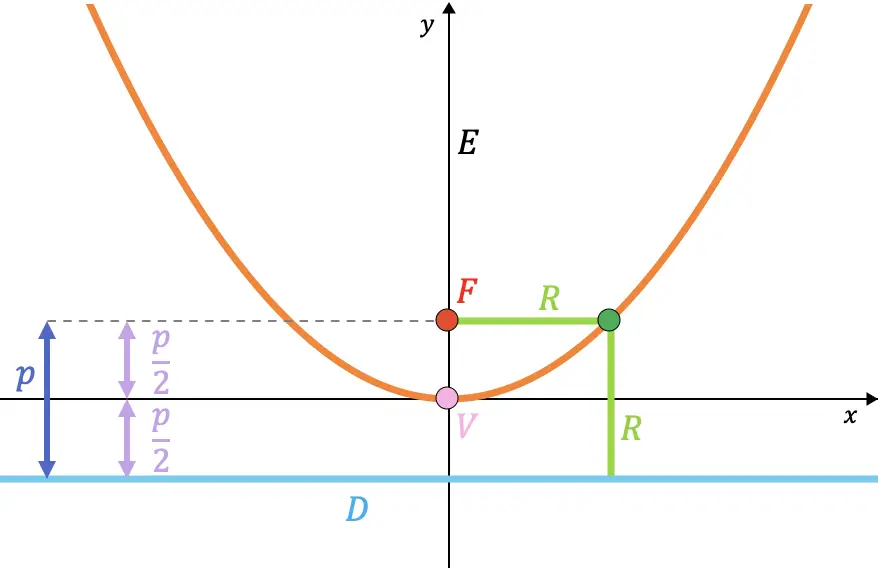
Sağ Taraf

Bir parabolün sağ tarafı , parabolün içindeki odak noktasından geçen ve doğrultmana paralel olan kiriştir.

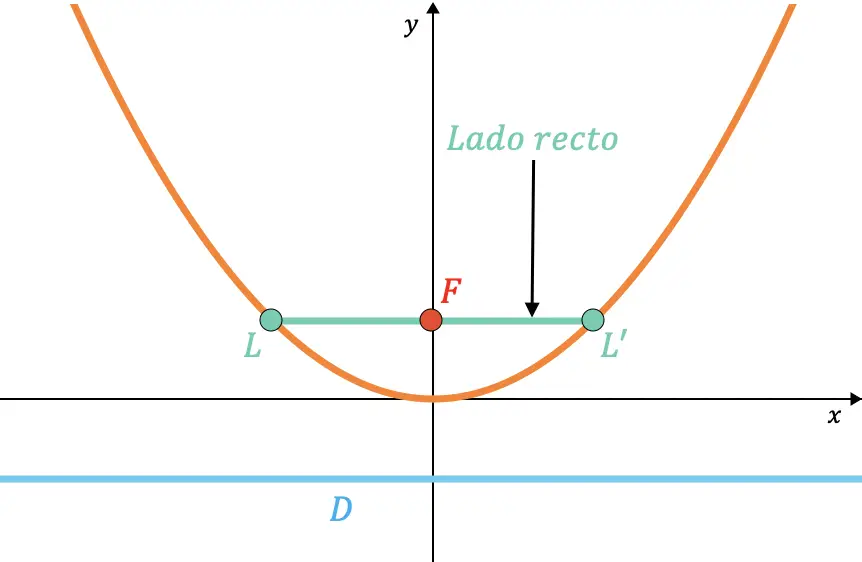
Benzer şekilde sağ tarafın uzunluğunun her zaman parametre değerinin iki katı olduğu gösterilebilir.

$p.$

$\lvert LL'\rvert = 2p$

Öte yandan, sağ tarafın uçlarından geçen parabole teğet olan iki çizgi, sağ tarafla 45° açı oluşturur ve parabolün tepesinde de kesişir.

parabol denklemleri

Bir parabol denklemi ikinci dereceden bir fonksiyon türüdür çünkü her zaman en az 1 kare terime sahip olması gerekir. Ayrıca bir parabolün denklemi onun yatay veya dikey yönüne bağlıdır.

Dolayısıyla analitik geometride bir parabolü matematiksel olarak ifade etmenin birkaç yolu vardır: kanonik veya indirgenmiş denklem , adi denklem ve parabolün genel denklemi .

Parabolün azaltılmış veya kanonik denklemi

İndirgenmiş veya kanonik denklemi diğer parabolik denklemlerden ayıran şey , parabolün tepe noktasının koordinatların orijini yani (0,0) noktası olmasıdır .

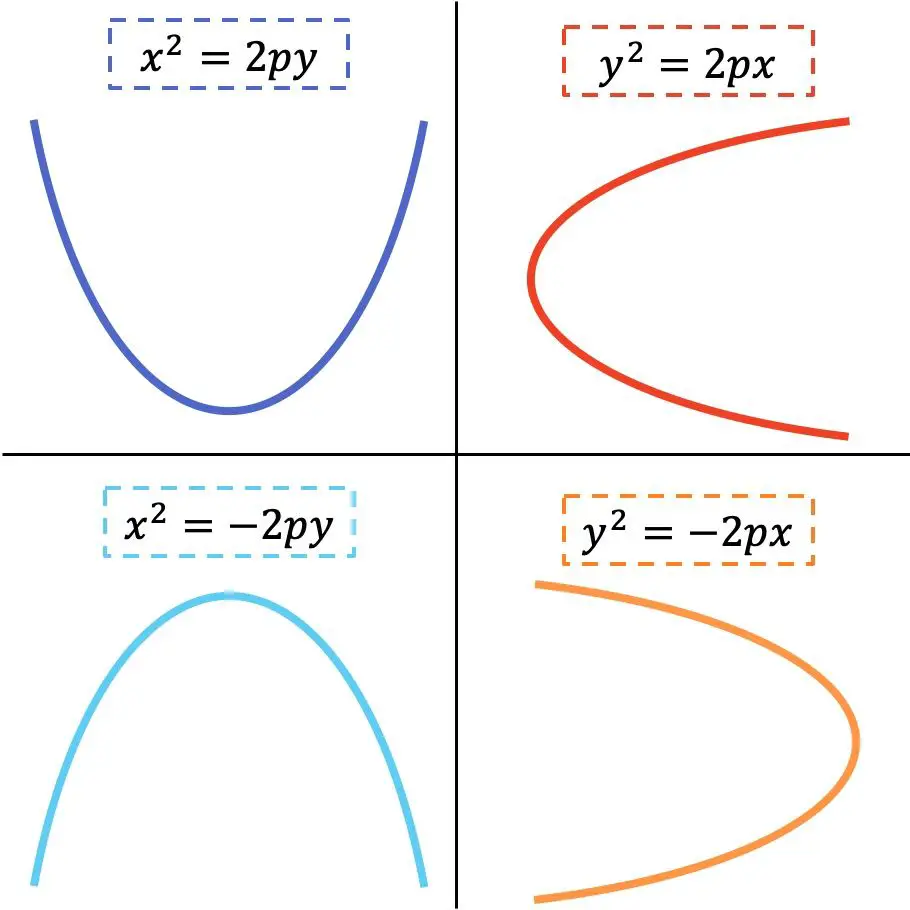
Parabolün indirgenmiş denkleminin şekli yatay veya dikey olmasına bağlıdır. 4 olası değişkenin gösterildiği aşağıdaki grafik gösterimine bakın:

Altın

$p$

parabolün karakteristik parametresidir.

Önceki görselde gördüğünüz gibi x değişkeninin karesi alındığında parabol dikey, y değişkeninin karesi alındığında ise parabol yatay oluyor. Öte yandan parabolün dallarının yönü denklemin işaretine bağlıdır.

Parabolün sıradan denklemi

Tepe noktası veya merkezi koordinatların orijinine (indirgenmiş veya kanonik denklem) karşılık geldiğinde parabol denkleminin nasıl göründüğünü az önce gördük, ancak tepe noktası ‘başlangıç noktası’ dışındaysa parabolün denklemi nedir?

Parabolün tepe noktası herhangi bir nokta olduğunda, parabolün ifadesi aşağıdaki gibi olan sıradan denklemi kullanırız :

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

parabolün merkezi veya tepe noktasının nokta olduğu yer

$V(x_0,y_0).$

Önceki denklem dikey olarak yönlendirilmiş parabole karşılık gelir, yani parabolün odak ekseni Y eksenine paraleldir.

Benzer şekilde, yatay olarak yönlendirilmiş bir parabol tanımlamak için (odak ekseni X eksenine paraleldir), parabolün sıradan denkleminin aşağıdaki varyantını kullanmalıyız:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

Daha önce olduğu gibi parabolün merkezi veya tepe noktası noktadır

$V(x_0,y_0).$

Parabolün genel denklemi

Şu ana kadar analiz ettiğimiz tüm parabol denklemleri yatay veya dikey parabolleri ifade etmek için kullanıldı. Ancak bir parabolün eğik veya eğik de olabileceği açıktır.

Bu tür parabolü ifade etmek için formülü aşağıdaki gibi olan genel parabol denklemini kullanırız:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

Yukarıdaki denklem ancak ve ancak katsayıların bir parabol olması durumunda

$A$

$C$

aynı anda sıfır değildir ve ayrıca aşağıdaki koşul karşılanır:

$B^2-4AC =0$

Bir parabolün tepe noktasını, odağını ve doğrultmanını denkleminden nasıl bulacağınıza dair örnek

Birçok parabol alıştırmasında ve probleminde, belirli bir parabolün tepe noktasını, odağını ve doğrultusunu hesaplamanız istenir. Bu nedenle, bunun nasıl yapıldığını bir örnek üzerinden görelim:

Aşağıdaki parabolün tepe noktasını, odağını ve doğrultmanını bulun:

$x^2 = 4y$

Bu tür parabol problemini çözmek için temel şey parabolün p parametresini belirlemektir . Bu durumda parabolün denklemi indirgenmiş veya kanonik denkleme (dikey parabol) karşılık gelir:

$x^2 = 2py$

Bu nedenle p parametresi:

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

Öte yandan, parabol indirgenmiş veya kanonik denklemi takip ettiğinden bu, tepe noktasının veya merkezinin koordinatların başlangıç noktasında olduğu anlamına gelir:

$\bm{V(0,0)}$

Parabolün tepe noktasını ve parametre değerini bildiğimizde odağını ve doğrultusunu kolaylıkla bulabiliriz.

Denklemin ikinci dereceden terimi x değişkenidir, böylece parabolün ekseni OY eksenine paralel olacaktır ve aslında tepe noktası (0,0) noktası olduğundan parabolün ekseni OY olacaktır. eksenin kendisi. O halde bir parabolün odağı her zaman parabolün ekseni üzerinde ve

$p/2$

parabolün tepesinden itibaren koordinatları şöyledir:

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

Benzer şekilde kılavuz çizgi de belirli bir mesafedeki yatay çizgi olacaktır.

$p/2$

koordinatların orijini olan parabolün tepe noktasından. Dolayısıyla çizginin denklemi şu şekilde olacaktır:

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

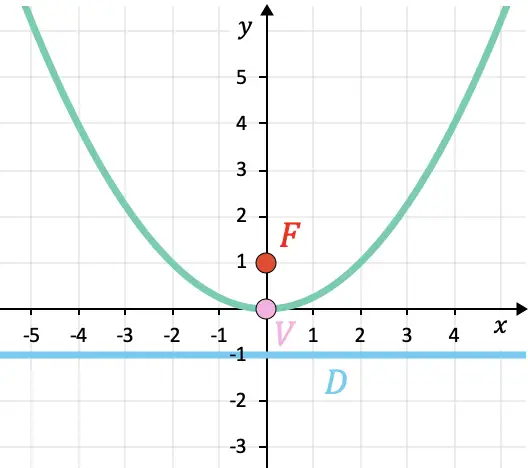
Sonuçları kontrol edebilmeniz için parabolün grafiği aşağıda verilmiştir:

Parabollerin özellikleri

Tüm paraboller aşağıdaki özelliklere sahiptir:

Parabol açık bir eğridir, başka bir deyişle sınırsız bir şekilde uzanan, hiçbir ortak noktası olmayan iki daldan oluşur.
Her parabolün, adı geçen parabolün tepe noktasının bulunduğu benzersiz bir simetri ekseni vardır.
Dikey olarak yönlendirilmiş bir parabol, dalları yukarı çıktığında dışbükeydir; aksine, dalları aşağı doğru inerse parabol içbükeydir.
Bir parabolün dışmerkezliği birliğe (1) eşdeğerdir. Dışmerkezlilik, bu durumda parabolün odak noktasından merkezine olan mesafenin tepe noktasından doğrultmana olan mesafeye bölünmesiyle hesaplanan bir katsayıdır (ve iki mesafe her zaman değerlerinde çakışır).
Önceki özelliğe göre tüm parabollerin benzer veya benzer olduğu sonucu çıkar.
Bir parabolün asimptotu yoktur.

parabolik uygulamalar

Artık bir benzetmenin anlamını çok iyi bildiğinize göre, merak ediyor olabilirsiniz… bir benzetmenin amacı nedir?

Size öyle gelmese de parabolün geometrik şekli gerçek hayatta çok yaygındır. Örneğin, özellikle basketbolda, top atıldığında çoğu zaman parabolik bir hareket yapar. Parabol denklemi, topun izlediği parabolik yolu analitik olarak incelemek için çok faydalıdır.

Çanağın başka bir uygulaması antenlerle ilgilidir (bu nedenle parabolik anten adı da budur). Simetri eksenine paralel parabolik şekilli bir cismin üzerine düşen her ışın doğrudan odağa doğru yansıdığı için yani parabolik antene giden tüm ışınlar odakta yoğunlaşır ve bu farklı şekillerde kullanılabilir. Bu nedenle bir benzetmenin odak noktası çok önemlidir.

Sabit çanak sorunları

1. Egzersiz

Denklemi aşağıdaki gibi olan parabolün tepe noktasını, odağını ve doğrultmanını hesaplayın:

$y^2 = 8x$

Çözüme bakın

Birincisi, parabol yatay olacaktır çünkü parabolün indirgenmiş veya kanonik denkleminin aşağıdaki ifadesini takip eder:

$y^2 = 2px$

Yani p parametresi:

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

Öte yandan, parabol indirgenmiş veya kanonik denklemi takip ettiğinden bu, tepe noktasının veya merkezinin koordinatların başlangıç noktasında olduğu anlamına gelir:

$\bm{V(0,0)}$

Parabolün tepe noktasını ve parametre değerini bildiğimizde odağını ve doğrultusunu kolayca hesaplayabiliriz.

Denklemin ikinci dereceden terimi değişkendir ve yani parabolün ekseni OX eksenine paralel olacaktır ve aslında tepe noktası (0,0) noktası olduğundan, l Parabolün ekseni şu şekilde olacaktır: OX ekseninin kendisi. O halde bir parabolün odağı her zaman parabolün ekseni üzerinde ve

$p/2$

Koordinatları şu şekilde olan parabolün tepesinden:

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

Aynı şekilde, kılavuz da uzaktadır

$p/2$

Koordinatların orijini olan ve odak eksenine dik olan parabolün tepe noktasından. Bu nedenle yönlendirme çizgisinin denklemi şu şekildedir:

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

Alıştırma 2

Denklemi aşağıdaki gibi olan parabolün tepe noktasını, odağını ve doğrultusunu bulun:

$(x-4)^2 = -16(y+1)$

Çözüme bakın

Parabol, formülü aşağıdaki gibi olan sıradan denklemine (eksen Y eksenine paralel) göre tanımlanır:

$(x-x_0 )^2 = 2p (y-y_0)$

Yani p parametresi:

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

Öte yandan, bu durumda parabolün sıradan denklemi, merkezinin koordinatların orijininde olmadığını ima ederken, parabolün tepe noktasının Kartezyen koordinatları, işareti değiştirilmiş parantez içindeki sayılardır. :

$\bm{V(4,-1)}$

Parabolün tepe noktasını ve parametre değerini bildiğimizde odağını ve doğrultusunu hesaplayabiliriz.

Denklemin ikinci dereceden terimi x değişkenidir, böylece parabolün ekseni OY eksenine paralel olur. Böylece bir parabolün odağı her zaman parabolün ekseni üzerinde ve

$p/2$

parabolün tepe noktasından itibaren, odak noktası koordinatları tepe noktasının koordinatları olacak şekilde eklenerek

$p/2$

dikey olarak:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

Benzer şekilde, direktrix de belli bir mesafede bulunan yatay çizgi olacaktır.

$p/2$

parabolün tepesinden. Bu nedenle yönlendirme çizgisinin denklemi şu şekildedir:

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

Alıştırma 3

Ekseni apsis eksenine paralel olan, tepe noktası V(5,2) olan ve odağı P(8,2) noktası olan parabolik denklemi belirleyin.

Çözüme bakın

Bu durumda parabolün tepe noktası koordinatların orijini değildir, dolayısıyla ifadenin parabolünü tanımlamak için sıradan denkleme ihtiyacımız var. Ayrıca parabolün odak ekseni x eksenine paraleldir; bu, parabolün yatay olarak yönlendirileceği (dallar sağa veya sola gidecek) ve dolayısıyla denklemin ikinci dereceden teriminin değişken olması gerektiği anlamına gelir. y :

$(y-y_0 )^2 = 2p (x-x_0)$