▷ Ortalama ve anlık değişim oranı (çözülmüş alıştırmalar)

Burada değişim hızının, ortalama değişim hızının ve anlık değişim hızının ne olduğunu açıklıyoruz. Değişim oranının nasıl hesaplanacağına dair birkaç örnek görebileceksiniz ve ayrıca değişim hızına ilişkin adım adım çözümlü alıştırmalar yapabileceksiniz.

Değişim oranı nedir?

Matematikte bir fonksiyonun değişim oranı (TV), bir fonksiyonun iki farklı noktadaki değerleri arasındaki farktır. Bu nedenle iki nokta arasındaki değişim oranının hesaplanması için fonksiyonun bu iki noktadaki değerlerinin çıkarılması gerekir.

$\text{TV}[a,b]=f(b)-f(a)$

Örneğin, bir fonksiyonun iki görüntüsü f(2)=1 ve f(5)=7 ise değişim oranları şöyledir:

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

Değişim oranının matematiksel anlamını az önce gördük, ancak ekonomide değişim oranı kavramı şu anlama gelir:

İktisatta iki değer arasındaki değişim oranı, yüzde olarak ifade edilen aralarındaki farktır, yani bir değişkenin farklı dönemler arasındaki değişim oranı onun göreceli değişimidir. Bu nedenle değişim oranını hesaplamak için iki farklı periyodun değerleri çıkarılır ve elde edilen sonuç başlangıç periyodu değerine bölünür.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

Örneğin, belirli hisselerin değeri bir ayda 35 Euro’dan 50 Euro’ya yükseldiyse değişim oranı şöyle olacaktır:

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

Değişim oranının iki olası anlamı göz önüne alındığında, bu makalede değişim oranının matematiksel tanımını anlamaya odaklanacağız. İki tür değişim oranı ayırt edilebilir: ortalama değişim oranı ve anlık değişim oranı. Aşağıda her türün açıklaması bulunmaktadır.

Ortalama değişim oranı

Bir fonksiyonun bir aralıktaki ortalama değişim oranı (TVM), bağımsız değişkeninin arttığı her bir birim için fonksiyonun arttırdığı (veya azalttığı) birim sayısıdır. Bu nedenle, bir fonksiyonun ortalama değişim hızı, fonksiyonun bir aralıktaki büyümesinin aynı aralığın genliğine bölünmesiyle hesaplanır.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

Ortalama değişim oranının nasıl hesaplandığını görebilmeniz için aşağıda adım adım bir örnek çözdük.

Bir fonksiyonun ortalama değişim oranını hesaplama örneği

Aşağıdaki fonksiyonun [2.5] aralığındaki ortalama değişim oranını hesaplayın:

$f(x) = x^2-1$

Öncelikle fonksiyonun x=2 ve x=5 noktasındaki değerini hesaplıyoruz:

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

Daha sonra aşağıdaki formülü uygulayarak fonksiyonun aralıktaki ortalama değişim oranını hesaplarız:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

TVM[2,5] sonucunun pozitif olması, fonksiyonun [2,5] aralığında büyüdüğü anlamına gelir. Öte yandan sonuç negatif olsaydı bu, fonksiyonun bu aralıkta azaldığı anlamına gelirdi.

Ortalama değişim oranının geometrik yorumu

Geometrik olarak, bir fonksiyonun bir aralıktaki ortalama değişim hızı, aralığın uç noktalarını birleştiren çizginin eğimini temsil eder.

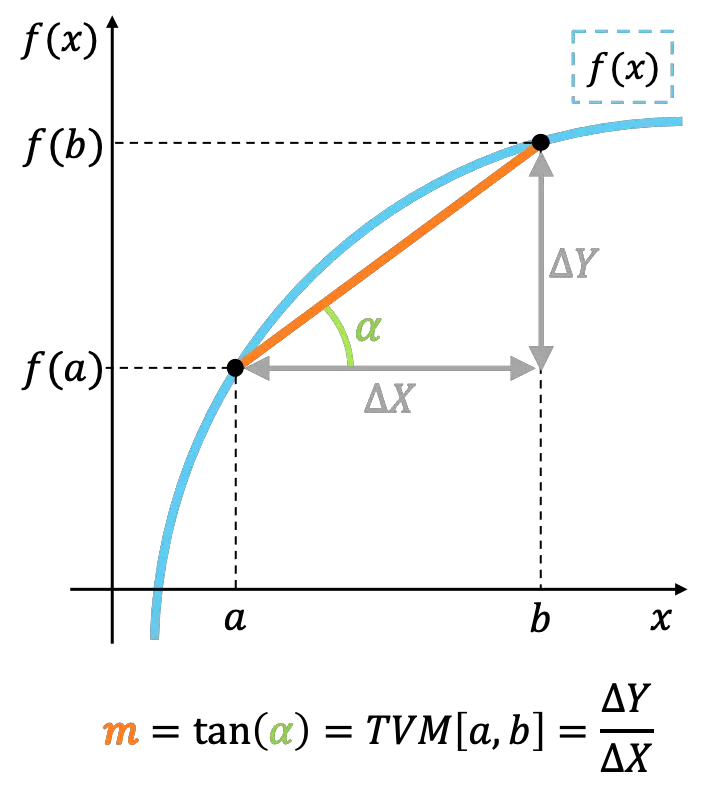
Anlık değişim oranı

Bir fonksiyonun bir noktadaki anlık değişim hızı (TVI), fonksiyonun bir aralıktaki göreceli artışının sonsuz küçük sınırıdır. Bu nedenle anlık değişim hızı , f(a+h)-f(a) bölümünün limitinin h sıfıra yaklaştığında çözülmesiyle hesaplanır.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

Anlık değişim oranının değeri pozitif, negatif veya sıfır olabilir ve bu, fonksiyonun o noktadaki sırasıyla arttığı, azaldığı veya aynı kaldığı anlamına gelir.

Bir fonksiyonun anlık değişim oranını hesaplama örneği

Aşağıdaki fonksiyonun x=2 noktasındaki anlık değişim oranını hesaplayın:

$f(x) = x^2$

Anlık değişim oranını hesaplamak için aşağıdaki formülü uygulamamız gerekir:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

Dikkate değer kimliği çözüyoruz:

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ Önemli kimliklerin formüllerini artık hatırlamıyorsanız, polinomlar konusunda uzmanlaşmış sitemizde tüm formülleri bulacaksınız: www.polinomios.org

Şimdi limiti çözmeye çalışalım:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

Ancak sıfır arasında sıfır belirsizlik buluyoruz, dolayısıyla:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ Bakınız: sıfır arasında sıfır belirsizliği olan bir limitin nasıl çözüleceği

Ve son olarak limiti çözüyoruz:

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

Henüz:

$\mathbf{TVI} \bm{(2) = 4}$

TVI(2) sonucunun pozitif olması fonksiyonun x=2’de arttığı anlamına gelir. Öte yandan sonuç negatif olsaydı bu, fonksiyonun bu aşamada azaldığı anlamına gelirdi.

Anlık değişim oranının geometrik yorumu

Geometrik olarak, bir fonksiyonun bir noktadaki anlık değişim hızı, fonksiyona aynı noktada teğet olan doğrunun eğimini temsil eder.

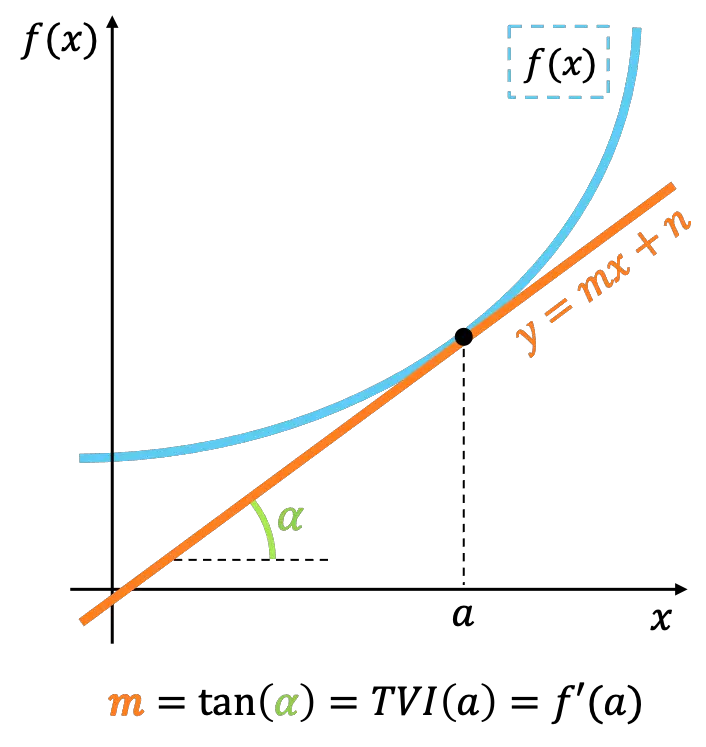
Yakından bakıldığında anlık değişim oranının anlamı bir fonksiyonun türevi kavramına eşdeğerdir. Böylece anlık değişim oranı aynı zamanda bir fonksiyonun bir noktadaki türevinin değerini hesaplamak için de kullanılır.

Değişim hızına ilişkin çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki fonksiyonun [1,3] aralığındaki değişim oranının değerini hesaplayın.

$f(x)=x^2-5$

Çözümü görün

Öncelikle fonksiyonun değerini aralığın sonlarında belirliyoruz:

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

Şimdi değişim oranı formülünü uyguluyoruz:

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

Alıştırma 2

Aşağıdaki fonksiyonun [1,4] aralığı boyunca ortalama değişim oranını (TVM) hesaplayın:

$f(x)=2x+1$

Çözümü görün

Önce fonksiyonun x=1 ve x=4 noktalarındaki görüntülerini hesaplıyoruz.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

Ve ortalama değişim oranı için formülü uyguluyoruz:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

Alıştırma 3

Aşağıdaki fonksiyonun [-1,3] aralığında ortalama değişim oranını bulun:

$f(x)=(x+1)^2$

Çözümü görün

Ortalama değişim oranını belirlemek için öncelikle f(-1) ve f(3)’ü hesaplamamız gerekir:

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

Şimdi ortalama değişim oranı formülünü kullanıyoruz:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

Alıştırma 4

Aşağıdaki grafikte gösterilen fonksiyonun [2,4] aralığındaki ortalama değişim oranını hesaplayın:

Çözümü görün

Ortalama değişim oranı için formülü uyguluyoruz:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

Formülde gördüğümüz gibi f(4) ve f(2) değerlerini bulmamız gerekiyor. Ve bu, fonksiyonun grafiksel gösterimine bakarak kolayca yapılabilir:

$f(4)=5$

$f(2)=1$

Artık fonksiyonun değerlerini bildiğimize göre bunları formülde yerine koyarız:

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

Alıştırma 5

Aşağıdaki fonksiyonun x=2 noktasındaki anlık değişim hızını hesaplayın:

$f(x)=3x$

Çözümü görün

Fonksiyonun x=2 noktasındaki anlık değişim oranını belirlemek için ilgili formülü uygularız:

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

Alıştırma 6

Aşağıdaki fonksiyonun x=1 noktasındaki anlık değişim oranını (TVI) belirleyin:

$f(x)=x^2+1$

Çözümü görün

Anlık değişim oranı için formülü uyguluyoruz:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

Daha sonra hesaplıyoruz

$f(1+h)$

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

Ve limitte bulunan değerleri değiştiriyoruz:

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

Dikkate değer ürünü çözüyoruz:

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

Şimdi limiti çözmeye çalışalım:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

Ancak sıfırın belirsiz formunu sıfıra bölerek buluruz, bu nedenle kesrin payının polinomunu çarpanlara ayırır ve basitleştiririz:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ Sıfır arasındaki sıfır belirsizliğini nasıl çözeceğinizi bilmiyorsanız, sıfır arasında sıfır belirsizliği olan bir limitin nasıl çözüleceğini yukarıdaki bağlantıdan tam olarak anlatabilirsiniz.

Ve son olarak limiti çözüyoruz:

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

Özetle, fonksiyonun x=1 noktasındaki anlık değişim hızı 2’ye eşittir.

$\mathbf{TVI} \bm{(1) = 2}$

Egzersiz 7

Aşağıdaki fonksiyonun x=2 noktasındaki anlık değişim oranını bulun:

$f(x)=4x^2-x+3$

Çözümü görün

İlk önce anlık değişim oranı formülünü kullanıyoruz:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

Hesaplıyoruz

$f(2+h)$

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

Ve limitte bulunan değerleri değiştiriyoruz:

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

Dikkate değer eşitliği hesaplıyoruz:

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

Pay üzerinde çalışıyoruz:

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

Şimdi limiti çözmeye çalışalım:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

Ancak sıfırın sıfıra bölünmesiyle oluşan belirsizliği elde ederiz, böylece polinomları çarpanlara ayırır ve basitleştiririz:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

Ve son olarak limiti çözüyoruz:

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

Henüz:

$\mathbf{TVI} \bm{(2) = 15}$

Değişim oranı nedir?

Ortalama değişim oranı

Bir fonksiyonun ortalama değişim oranını hesaplama örneği

Ortalama değişim oranının geometrik yorumu

Anlık değişim oranı

Bir fonksiyonun anlık değişim oranını hesaplama örneği

Anlık değişim oranının geometrik yorumu

Değişim hızına ilişkin çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Egzersiz 7

Yorum bırakın Yanıtı iptal et