Düzenli matris

Bu sayfada normal matrisin ne olduğunu ve normal matris örneklerini göreceksiniz. Ayrıca bu tür matrislerin özelliklerini ve adım adım çözülmüş alıştırmaları bulacaksınız.

Normal matris nedir?

Normal dizi tanımı şöyledir:

Normal bir matris, eşlenik transpoz matrisi ile çarpılan karmaşık bir matris olup, eşlenik transpozun tek başına çarpımına eşittir.

A\cdot A^*=A^*\cdot A

Altın

A^*

eşlenik devrik matrisidir

A

.

Bununla birlikte, eğer bunlar gerçel sayı matrisleri ise, önceki koşul, bir matrisin devri ile değişmekte olduğunu söylemek anlamına gelir, yani:

A\cdot A^t=A^t\cdot A

Çünkü açıkçası, gerçek bir matrisin eşlenik devrik matrisi, basitçe devrik (veya devrik) matristir.

Normal matris örnekleri

Karmaşık sayılarla örnek

Aşağıdaki 2×2 boyutlu karmaşık kare matris normaldir:

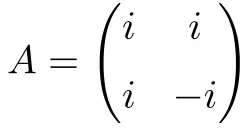
2x2 boyutunda karmaşık sayılara sahip normal matris örneği

Normalliğinin gösterimi aşağıda ekte verilmiştir:

\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}

\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}

Gerçek sayılarla örnek

2. mertebeden gerçek sayılara sahip aşağıdaki kare matris de normaldir:

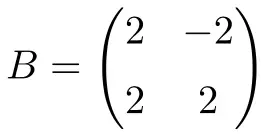
2x2 boyutlu gerçek sayılara sahip normal matris örneği

Bu durumda sadece reel sayılar olduğundan normal olduğunu kanıtlamak için matrisin devrikle değiştirilebilir olduğunu doğrulamak yeterlidir:

\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}

\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}

Normal matrislerin özellikleri

Normal matrisler aşağıdaki özelliklere sahiptir:

  • Tüm normal matrisler köşegenleştirilebilir matrislerdir.
  • Benzer şekilde antihermitian matris de normal bir matristir.
  • A normal bir matris ise, eşlenik transpoze matrisi A*’nın özdeğerleri (veya özdeğerleri), A’nın eşlenik özdeğerleridir.

\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i

\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i

  • Normal matrislerde, farklı özdeğerlerle ilişkili özvektörler (veya özvektörler) diktir.
  • Bir matris yalnızca gerçek sayılardan oluşuyorsa ve simetrikse aynı zamanda normal bir matristir.
  • Son olarak, gerçel sayılardan oluşan herhangi bir ortogonal matris de normal bir matristir.

Normal matrisler için çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki 2 × 2 boyutlu karmaşık matrisin normal olduğunu doğrulayın:

\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}

Matrisin normal olduğunu göstermek için önce eşlenik devrini hesaplamamız gerekir:

\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}

Şimdi doğrulamayı A matrisini A* matrisiyle her iki olası yönde çarparak yapıyoruz:

\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}

\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}

Her iki çarpımın sonucu aynı olduğundan A matrisi normaldir.

Alıştırma 2

Aşağıdaki 2 × 2 boyutunda gerçek matrisin normal olduğunu gösterin:

\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}

Bu durumda yalnızca reel sayıların olduğu bir ortamla uğraştığımız için, A matrisi ile onun devriği arasındaki matris çarpımının, çarpmanın yönü ne olursa olsun aynı sonucu verdiğini doğrulamak yeterlidir:

\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}

\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}

Her iki çarpımın sonucu aynı olduğundan A matrisi normaldir.

Alıştırma 3

Aşağıdaki 2. mertebeden karmaşık sayılar matrisinin normal olup olmadığını belirleyin:

\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}

Matrisin normal olup olmadığını kontrol etmek için önce eşlenik devrini hesaplamamız gerekir:

\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}

Şimdi A matrisinin ve onun eşlenik devriğinin değiştirilebilir olup olmadığını kontrol edeceğiz:

\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}

\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}

Her iki çarpımın sonucu aynı olduğundan A matrisi normaldir.

Alıştırma 4

Aşağıdaki 3×3 boyutlu gerçek matrisin normal olduğunu doğrulayın:

\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}

Matris tamamen gerçek elemanlardan oluştuğundan, A matrisi ile onun devri arasındaki matris çarpımının çarpma yönünden bağımsız olduğunu doğrulamak yeterlidir:

\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}

\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}

Her iki çarpımın sonucu aynı olduğundan A matrisi normaldir.

Alıştırma 5

Aşağıdaki 3×3 mertebesindeki karmaşık matrisin normal olup olmadığını belirleyin:

\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}

İlk olarak matrisin eşlenik transpozunu hesaplıyoruz:

\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}

Şimdi A matrisi ile onun eşlenik devriği arasındaki matris çarpımlarını her iki olası yönde de yapmamız gerekiyor. Bununla birlikte, A’nın eşlenik devrik matrisi, A matrisinin kendisine eşittir, dolayısıyla bu bir Hermit matrisidir. Ve bu nedenle, normal matrislerin özelliklerinden A’nın normal bir matris olduğu sonucu çıkar , çünkü her Hermit matrisi normal bir matristir.

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top