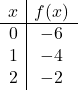Mutlak Değer Fonksiyonları -

Bu sayfada mutlak değer fonksiyonunun ne olduğu açıklanmaktadır. Ayrıca parçalı mutlak değer fonksiyonunun nasıl tanımlanacağını ve bu tür fonksiyonların bir grafik üzerinde nasıl temsil edileceğini de öğreneceksiniz. Ayrıca mutlak değerli fonksiyon örnekleri ile görecek, alıştırmalar ve adım adım çözülen problemler ile pratik yapabileceksiniz.

Mutlak değerli fonksiyonlar nelerdir?

Mutlak değer fonksiyonunun tanımı aşağıdaki gibidir:

Bir fonksiyonun mutlak değeri, tüm görüntülerini pozitif görüntülere dönüştürür. Bu nedenle mutlak bir fonksiyonun yolu hiçbir zaman negatif değerlere sahip olamaz.

Aşağıdaki fonksiyon mutlak değer fonksiyonuna bir örnektir:

$f(x)=\lvert 5x \rvert$

Fonksiyonu bir noktada değerlendirirken olumlu bir sonuç elde edersek, bu olumlu kalır:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

Öte yandan sonuç negatifse pozitif olur:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Mutlak değer fonksiyonları genellikle lisede verilmektedir çünkü özellikleri onların anlaşılmasını biraz zorlaştırmaktadır.

Mutlak değeri olan bir fonksiyon parçalı olarak nasıl tanımlanır?

Mutlak değerli bir fonksiyon parçalı fonksiyon olarak ifade edilebilir. Bunu yapmak için fonksiyonun negatif olan aralıklardaki işaretini değiştirmeniz gerekir.

Mutlak değer fonksiyonundan parçalı fonksiyona nasıl geçileceğine dair bir örnek görelim:

Aşağıdaki fonksiyonu mutlak değerle parçalı fonksiyon olarak ifade edin:

$f(x) = \lvert 4 - x^2 \rvert$

Yapmamız gereken ilk şey fonksiyonun ne zaman negatif olduğunu belirlemektir. Bunu yapmak için cebirsel ifadeyi mutlak değerde 0’a eşitleyip denklemi çözüyoruz:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

Artık satırda elde edilen değerleri temsil ediyoruz:

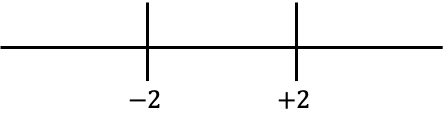
Ve satırın her aralığında hangi işaretin mutlak değeri olmayan fonksiyona sahip olduğuna bakıyoruz:

$x<-2$

Örneğin -2’den küçük herhangi bir noktayı alırız

$x=-3:$

$4-(-3)^2$

$-5$

Olumsuz

$-2 < x < 2$

Örneğin -2 ile +2 arasında herhangi bir noktayı alırız

$x=0:$

$4-0^2$

$+4$

Pozitif

$x>2″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> Örneğin 2’den büyük herhangi bir noktayı alırız <p class=$ $x=3:$

$4-3^2$

$-5$

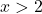
Olumsuz

Gördüğümüz gibi mutlak değeri olmayan fonksiyon aralıklarda negatif olacaktır.

$x<-2$

$x>2.” title=”Rendered by QuickLaTeX.com” height=”14″ width=”47″ style=”vertical-align: -2px;”> Bu nedenle fonksiyonun işaretini bu aralıklarda değiştirerek tirelerle ifade etmemiz gerekir: 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”> 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”> Bazı aralıklarla eşitliği eklemeniz gerektiğini unutmayın. Örneğin, burada onu ikinci aralığa koyuyoruz <p class=$ $-2 \le x \le 2$

. Ama tüm kritik noktalarda eşitlik olduğu sürece istediğiniz aralığa yerleştirebilirsiniz. Yani fonksiyonu şu şekilde tanımlasaydık aynı olurdu:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

Mutlak değerli bir fonksiyon nasıl temsil edilir?

Mutlak değeri olan bir fonksiyonu grafik üzerinde temsil etmek için aşağıda açıklanan adımları izlememiz gerekir:

Fonksiyonu sanki mutlak değeri yokmuş gibi temsil edin.
Fonksiyonun negatif olduğu yani X ekseninin altında kaldığı aralıklarda simetrik fonksiyonu çizin.
Fonksiyonun X ekseninin altındaki kısmını silin.

Mutlak değeri olan bir fonksiyonun grafiğinin nasıl çizileceğine dair bir örnek görelim

Aşağıdaki fonksiyonun mutlak değer grafiğini çizin:

$f(x) = \lvert -x+2 \rvert$

Bir fonksiyonu mutlak değerli olarak temsil etmek için öncelikle fonksiyonu mutlak değeri olmadan temsil etmemiz gerekir. Bu nedenle fonksiyon değerleri tablosunu mutlak değer olmadan yapıyoruz:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

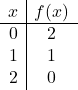
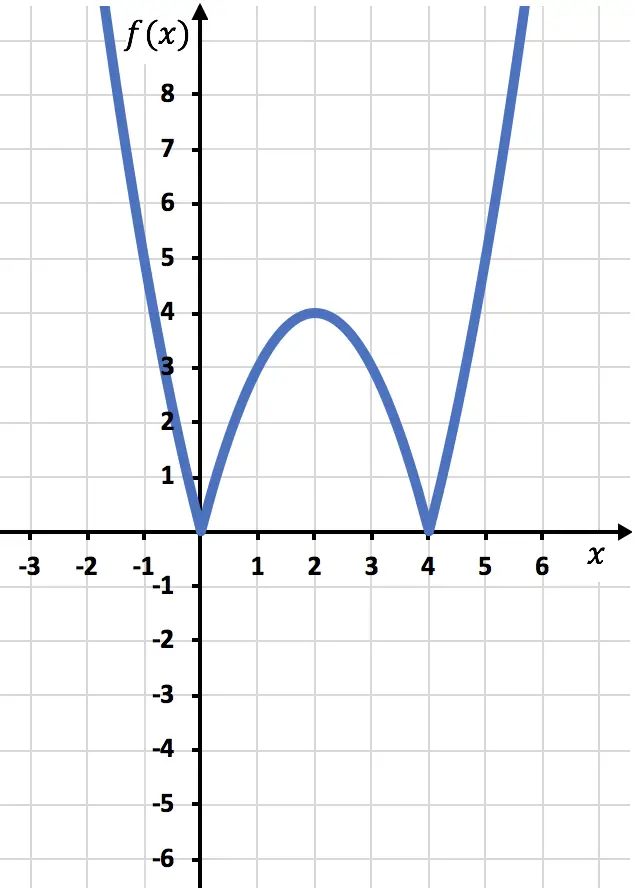
Noktaların grafiğini çiziyoruz ve normal bir fonksiyonmuş gibi çizgiyi çiziyoruz:

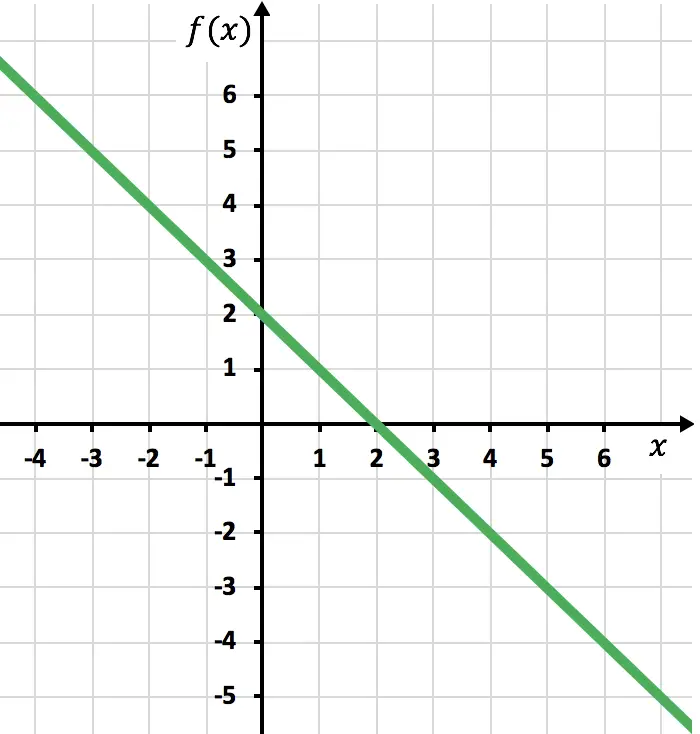
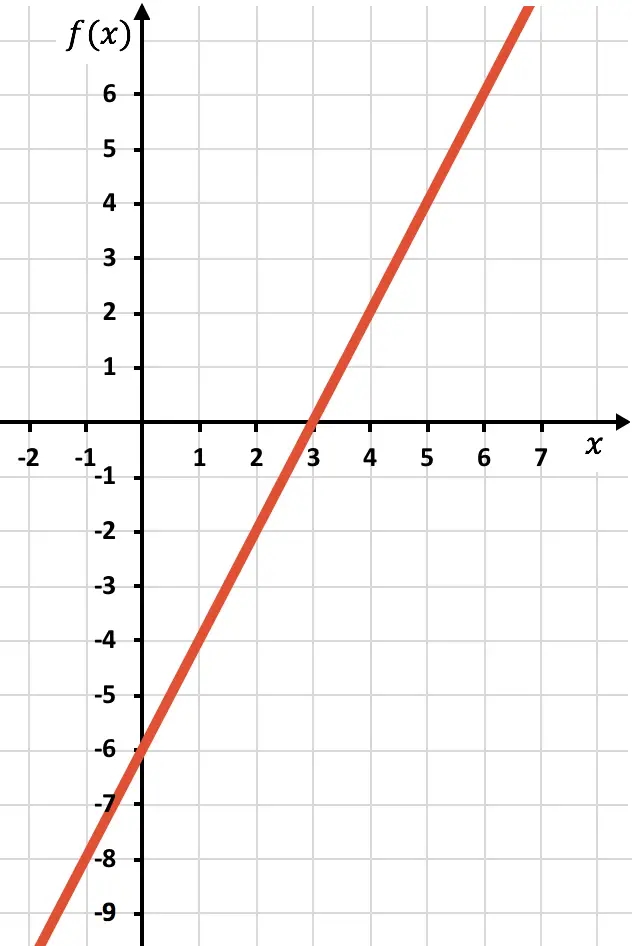
Şimdi simetrik fonksiyonu fonksiyonun negatif olduğu yere yani x ekseninin altında olduğu yere çizmemiz gerekiyor. Bu nedenle x=2’den başlayarak fonksiyonu tersine çeviririz:

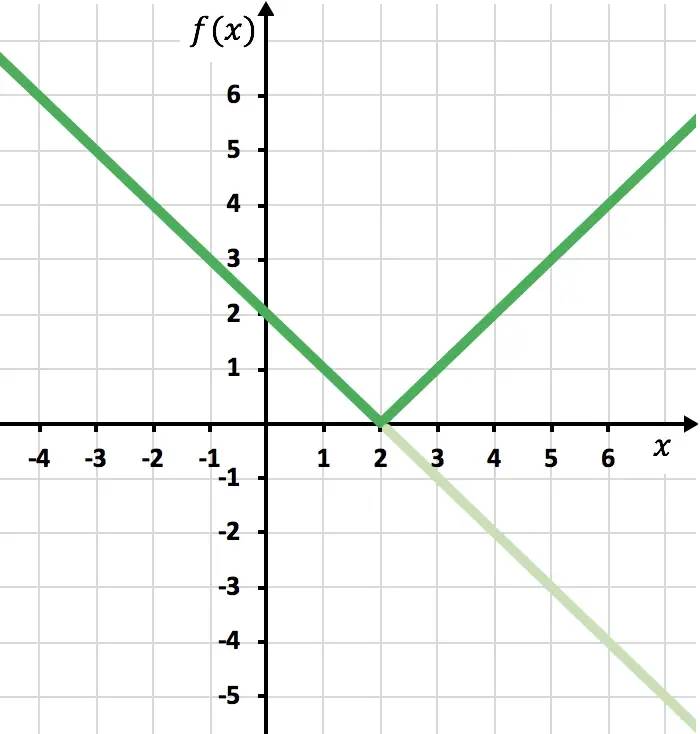
mutlak değeri olan bir fonksiyonun nasıl temsil edileceği

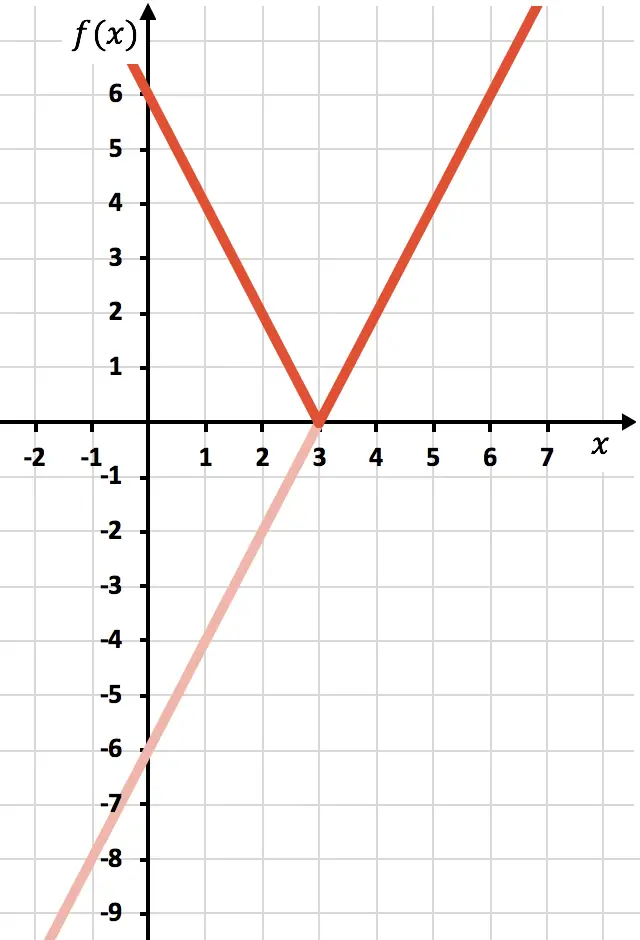
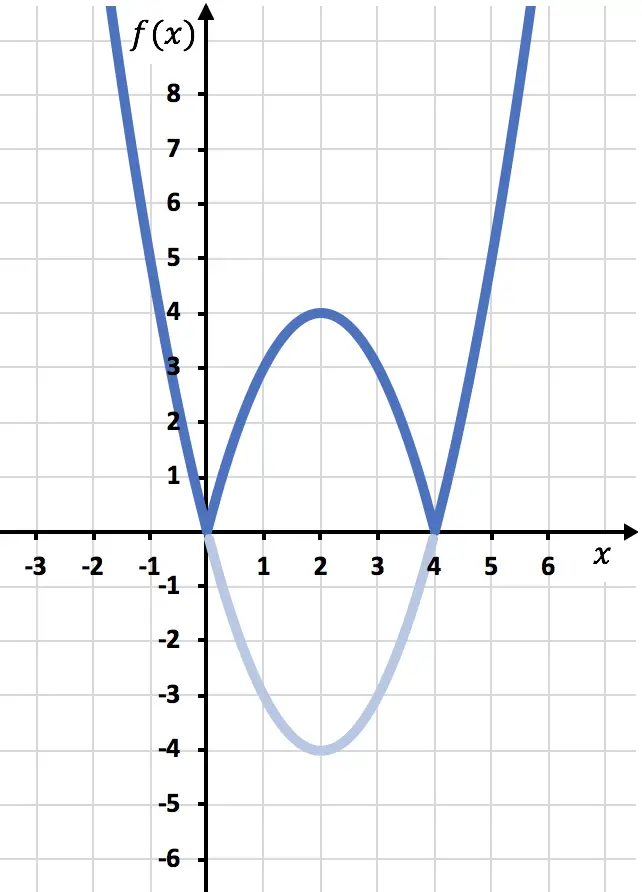
Ve son olarak X ekseninin altında bulunan fonksiyonun izini ortadan kaldırıyoruz:

mutlak değeri olan bir fonksiyonun grafiği nasıl çizilir

Ve bu şekilde zaten fonksiyonu mutlak değerle temsil etmiş oluyoruz. Gördüğünüz gibi değişen tek şey fonksiyonun OX ekseninin altındaki kısmını ters çevirmemiz gerektiği. Bu nedenle mutlak değeri olan herhangi bir fonksiyonun grafiği her zaman pozitif yarı Y ekseninin yanında yer alacaktır.

Öte yandan kavramları tekrar gözden geçirmek gerekirse, grafikten önceki mutlak değer fonksiyonunun tanım kümesinin tamamen reel sayılardan oluştuğu sonucunu çıkarabiliriz. Öte yandan söz konusu fonksiyonun mutlak değere sahip aralığı veya aralığı yalnızca pozitif sayılardan ve sıfırlardan oluşur.

Mutlak değer fonksiyonlarına ilişkin çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki fonksiyonu mutlak değerle parçalı fonksiyon olarak ifade edin:

$f(x)= \lvert -x+3 \rvert$

Çözümü görün

Öncelikle fonksiyonun ne zaman negatif olduğuna bakmamız gerekiyor. Bunu yapmak için mutlak değeri sıfıra eşitliyoruz ve denklemi çözüyoruz:

$-x+3=0$

$x=3$

Satırda bulunan değeri temsil ediyoruz:

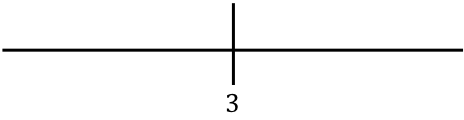
Şimdi, fonksiyonun çizginin her bölümünde gerçekte hangi işarete sahip olduğunu bulmak için fonksiyonun her aralığındaki bir noktayı mutlak değer olmadan değerlendireceğiz:

$x<3$

Örneğin 3’ten küçük herhangi bir noktayı alırız

$x=0:$

$-0+3$

$+3$

Pozitif

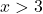$x>3″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”> <p class=$ Örneğin 3’ten büyük herhangi bir noktayı alırız

$x=4:$

$-4+3$

$-1$

Olumsuz

Mutlak değeri olmayan fonksiyon x>3 aralığında negatif olacaktır. Bu nedenle, bu aralıkta işaretini değiştirerek fonksiyonu kısa çizgilerle ifade etmeliyiz:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Alıştırma 2

Aşağıdaki fonksiyonun mutlak değerli parçalı ifadesini bulun:

$f(x)= \lvert 3x^2-75 \rvert$

Çözümü görün

Yapmamız gereken ilk şey fonksiyonun ne zaman negatif olduğunu belirlemektir. Bunu yapmak için mutlak değer argümanını sıfıra eşitlememiz ve denklemi çözmemiz gerekiyor:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

Şimdi sağda elde edilen fonksiyonun köklerini temsil ediyoruz:

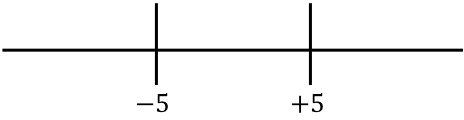
Ve satırın her aralığında hangi işaretin mutlak değeri olmayan fonksiyona sahip olduğuna bakıyoruz:

$x<-5$

Örneğin -5’ten küçük herhangi bir noktayı alırız

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Pozitif

$-5 < x < 5$

Örneğin -5 ile +5 arasında herhangi bir noktayı alırız

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

Olumsuz

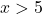$x>5″ title=”Rendered by QuickLaTeX.com” height=”15″ width=”42″ style=”vertical-align: -2px;”> <p class=$ Örneğin 5’ten büyük herhangi bir noktayı alırız

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

Pozitif

Bu nedenle mutlak değeri olmayan fonksiyon yalnızca -5<x<5 aralığında negatif olacaktır. Bu nedenle, bu aralığın yalnızca işaretini değiştirerek fonksiyonu kısımlar halinde ifade etmemiz gerekir:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”> 5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”> <div class=$

Alıştırma 3

Bir fonksiyonu mutlak değerle temsil etmek için öncelikle fonksiyonu mutlak değer olmadan temsil etmelisiniz:

Bu bir afin fonksiyondur, dolayısıyla onu grafiksel olarak temsil etmek için bir değerler tablosu oluşturmanız gerekir:

Şimdi simetrik fonksiyonu fonksiyonun negatif olduğu yere yani X ekseninin altında olduğu yere çizmemiz gerekiyor. Bu nedenle, fonksiyonu x=3’ten geriye doğru çeviririz:

Son olarak fonksiyonun X ekseninin altında bulunan kısmını ortadan kaldırıyoruz:

Alıştırma 4

Mutlak değerli bir fonksiyonu temsil etmek için önce mutlak değeri olmayan fonksiyonu çizmeliyiz.

Bu ikinci dereceden bir fonksiyondur. Bu nedenle, onu temsil etmek için parabolün tepe noktasının X koordinatını formülüyle hesaplamalıyız:

Şimdi bir değerler tablosu oluşturuyoruz. Bunu yapmak için değerini hesaplıyoruz.

Şimdi fonksiyonu negatif olduğu yerde, yani OX ekseninin altında olduğu yerde simetriye göre çevirmemiz gerekiyor. Bu nedenle fonksiyonu x=0’dan x=4’e tersine çeviririz: