▷ Tam kare üç terimli nedir? (örnekler)

Bu sayfada tam kare üç terimlinin ne olduğunu ve nasıl açıklandığını açıklıyoruz. Ek olarak, çeşitli örnekleri görebileceksiniz ve adım adım tam kare trinomiyal egzersizlerle pratik yapabileceksiniz.

Tam kare trinom nedir?

Açıkçası, tam kare üç terimlinin anlamını görmeden önce, üç terimlilerin ne olduğunu bilmeniz gerekir, bu nedenle devam etmeden önce bu bağlantılı sayfaya (ayrıntılı olarak açıklandığı yer) bir göz atmanızı öneririm.

Dolayısıyla, tam kare bir trinomiyalin tanımı aşağıdaki gibidir:

Matematikte, TCP olarak da bilinen mükemmel kare trinom , bir binomun karesi alınarak elde edilen trinomdur.

Bu nedenle, bir tam kare trinomial, iki tam kareye sahip bir polinom ve bu karelerin tabanlarının çift çarpımı olan başka bir terimden oluşur.

Yukarıdaki iki formülden de görebileceğiniz gibi, tam kare trinomial iki önemli kimlikten (veya dikkate değer ürünlerden) elde edilir, bu yüzden bu kadar önemlidir. Spesifik olarak, bir toplamanın karesini veya bir çıkarmanın karesini çözerken mükemmel bir kare trinomiyal bulunur.

Mükemmel Kare Trinomial Örnekleri

Tam kare üçlü terim kavramını anlamayı tamamlamak için 2 örneği adım adım açıklayacağız:

örnek 1

$x^2+6x+9$

Bu örnek bir tam kare üç terimlidir çünkü cebirsel ifadesinde iki tam kare vardır (yani bunların tam bir karekökü vardır), çünkü

$x^2$

ve 9 eşittir

$x$

ve 3 sırasıyla ikinin kuvvetine yükseltildi:

$(x)^2 = x^2$

$(3)^2 = 9$

Ve dahası, üç terimlinin kalan son terimi

$(6x)$

Önceki iki karenin tabanlarının birlikte ve 2 ile çarpılmasıyla elde edilir:

$2\cdot x \cdot 3 = 6x$

Yani bu alıştırmadaki tüm dikkate değer kimlik şu şekilde olacaktır:

$(x+3)^2 =x^2+6x+9$

Örnek 2

$16x^2-40x+25$

Bu diğer örnek de bir tam kare trinomialdir çünkü gerekli 3 koşul karşılanmıştır: iki terim iki tam kareye karşılık gelir ve başka bir terim bu karelerin tabanlarının birbiriyle ve 2 ile çarpılmasının sonucudur.

$(4x)^2 = 16x^2$

$(5)^2 = 25$

$2\cdot 4x \cdot 5 =40x$

Bu durumda, tam kare üç terimli negatif bir tek terimliye sahiptir, bu nedenle kare farkın dikkate değer eşitliğinin geliştirilmesine karşılık gelir:

$(4x-5)^2 = 16x^2-40x+25$

Mükemmel Kare Trinomial Nasıl Çarpanlarına Ayrılır?

Cebirde çok yaygın bir problem, tam kare trinomiyalin (PCT) çarpanlara ayrılmasıdır. Bunun ne anlama geldiğini bilmiyorsanız, bir polinomu çarpanlara ayırmak, onun ifadesini faktörlerin çarpımına dönüştürmek anlamına gelir.

Bu nedenle, bu tip cebirsel üç terimliyi çarpanlarına ayırmak için aşağıdaki kurallara uyulmalıdır:

Üç terimlinin iki tam kareye sahip olması gerekir; bunlara
$a^2$

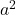
Ve

$b^2.$
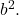
Üç terimlinin kalan üçüncü terimi, iki tam karenin tabanlarının çift çarpımına eşit olmalıdır; bu, matematiksel olarak şu ifadeye karşılık gelir:
$2\cdot a \cdot b.$
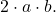
Çarpanlarına ayrılmış üç terimli olacaktır
$(a+b)^2$

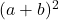
tam kare üç terimlinin tüm terimleri pozitifse, aksi takdirde karelerin tabanlarının çift çarpımı negatif işarete sahipse, çarpanlara ayrılmış üç terimli şu şekilde olacaktır:

$(a-b)^2.$

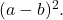
Prosedürü anlamayı tamamlamak için bir alıştırmayı adım adım çözeceğiz:

Aşağıdaki tam kare üç terimliyi çarpanlarına ayırın:

$x^2-12x+36$

Yapmamız gereken ilk şey, trinomialin iki elemanının tam kare olup olmadığını, yani karekökünün ondalık sayı verip vermediğini tespit etmektir. Bu problemde

$x^2$

değişkenin karesidir

$x$

ve 36, 6’nın karesidir:

$\sqrt{x^2} = x$

$\sqrt{36} = 6$

Dolayısıyla trinomialin iki tam karesi vardır.

İkinci olarak, ara terimin önceki adımda hesaplanan iki kökün çift çarpımına eşdeğer olup olmadığını kontrol etmeliyiz:

$2 \cdot x \cdot 6 = 12x$

Bu kurala da saygı duyulur.

O zaman tüm koşullar yerine getirilir. Bu nedenle, çarpanlara ayrılmış mükemmel kare trinomial, bulunan iki kökün oluşturduğu binomdur (

$x$

ve 6 sayısının karesi:

$x^2-12x+36=(x-6)^2$

Ara terim negatif olduğundan parantez içine eksi işareti de koymalıyız. Öte yandan, eğer pozitif olsaydı, bir miktar eklememiz gerekecekti:

$x^2+12x+36=(x+6)^2$

Mantıksal olarak, çarpanlara ayırma karmaşık bir prosedürdür, bu nedenle aşağıdaki alıştırmayı yapmaya çalışmanın yanı sıra, çarpanlara ayırma polinomlarının bu örneklerine bakmanızı öneririm. Bu bağlantıda ayrıca sadece üç terimlileri çarpanlarına ayırmak için değil, aynı zamanda her tür polinomu da aynı hızla çarpanlara ayırmak için kullanılan bir yöntemi açıklıyoruz.

Tam kare trinomiyalin çözülmüş alıştırmaları

İlgili formülü uygulayarak aşağıdaki üç terimlileri kare binomlara dönüştürün:

$\text{A)} \ x^2+8x+16$

$\text{B)} \ x^2-14x+49$

$\text{C)} \ x^4-20x^2+100$

$\text{D)} \ 81x^2+90x+25$

$\text{E)} \ 64x^4-176x+121$

Çözümü görün

Tam kare üç terimliyi kare binomun kuvvetine dönüştürmek için, bir toplamın karesi ile bir farkın karesinin dikkate değer özdeşliklerine ilişkin formülleri kullanmanız gerekir; bunlar:

$(a+b)^2 = a^2+2ab+b^2$