Monomiyaller - Mathority

Burada tek terimlilerle ilgili bilmeniz gereken her şeyi açıklıyoruz: ne oldukları, parçalarının ne olduğu (ve bunların nasıl tanımlanacağı), farklı tek terim türleri, tek terimli işlemler nasıl hesaplanır, bir tek terimlinin sayısal değeri. .. Ayrıca tek terimlilerin adım adım çözüldüğü örnekleri ve alıştırmaları görebileceksiniz.

Monomiyaller nedir?

Matematikte tek terimli tanımı şu şekildedir:

Monom, sayı ve harflerin birleşiminden oluşan cebirsel bir ifadedir. Daha kesin olarak, bir monom, bir sayı ile bir veya daha fazla değişkenin (harflerin) üslere yükseltilmiş çarpımından oluşur.

Örneğin, 7x ³ y ² terimine tek terimli denir çünkü bir sayıya (7) ve farklı harflere (x, y) sahiptir.

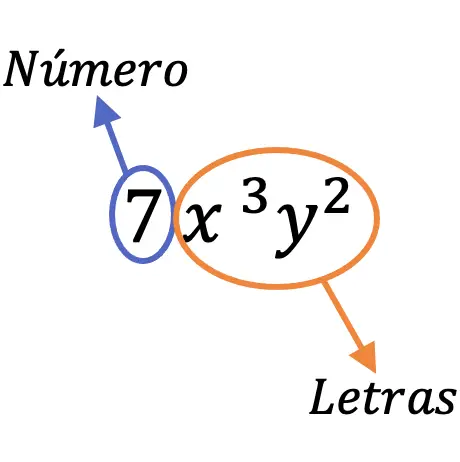
Bir monomialin parçaları

Artık tek terimlinin anlamını gördüğümüze göre, tek terimlinin tüm parçalarının ne olduğuna bakalım:

Katsayı : Monomiyalin değişkenlerini (veya harflerini) çarpan sayıdır.
Değişken : Tek terimde görünen harflerin her biri.
Değişmez kısım : monomial’i oluşturan tüm değişkenlere ilgili tüm üsleriyle karşılık gelir.
Derece : Tek terimliyi oluşturan harflerin tüm üslerinin toplamından oluşur.

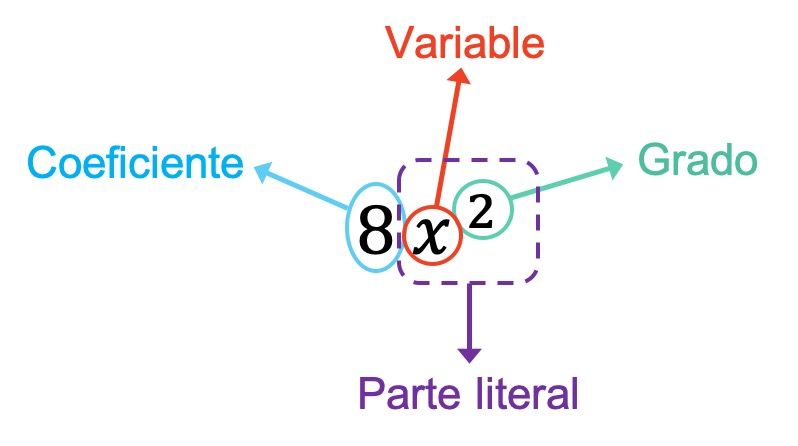
Yukarıdaki örnekte monomialin katsayısı değişkenleri çarpan sayı olduğundan 8’dir. Ayrıca bu durumda tek terimlinin yalnızca bir değişkeni vardır, o da x’tir. Yani, monomun gerçek kısmı bu değişken artı onun üssü olan x ^2’den oluşur. Son olarak tek terimlinin derecesi 2’dir çünkü sahip olduğu tek üs odur.

Şimdi bir monomiyalin bölümleri üzerinde aşağıdaki alıştırmayı çözmeye çalışın:

Aşağıdaki tek terimlinin tüm parçalarını tanımlayın:

$5x^4y^2z$

Çözüme bakın

İfadenin tek terimli bileşenleri şunlardır:

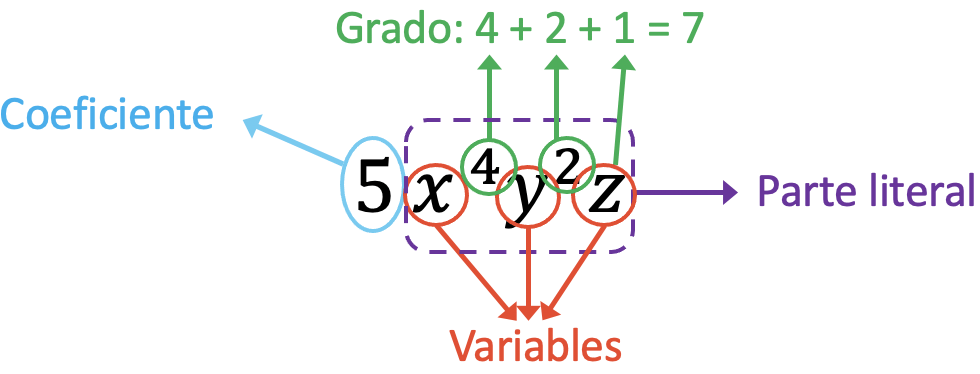
monomiyallerle ilgili adım adım çözülen alıştırmalar

Harfleri çarpan terim olduğundan problemdeki monomialin katsayısı 5’tir. Öte yandan bu monomialin değişkenleri x, y, z’dir. Üçüncüsü, tek terimlinin gerçek kısmı x ⁴ y ² z ifadesine karşılık gelir. Ve son olarak tek terimlinin derecesi değişkenlerin tüm üslerinin toplamına yani 7’ye (4+2+1=7) eşittir.

Bir harfin üssü olmadığında bunun aslında üssünün 1 olduğu anlamına geldiğini unutmayın. Bu nedenle problemin monomunun derecesini hesaplamak için z değişkeninin üssünü temsil eden bir birim ekliyoruz.

Tek terimli türleri

Her biri kendi özelliklerine sahip farklı monom türleri vardır. En önemli monomlar benzer monomlar, homojen monomlar, heterojen monomlar ve zıt monomlardır. Daha sonra her türün özelliklerini göreceğiz.

benzer monomlar

Benzer monomlar, aynı değişmez kısma sahip olan monomlardır. Bu nedenle, iki veya daha fazla tek terimli sayılar aynı harflere ve üslere sahip olduklarında benzerdir.

Örneğin aşağıdaki iki tek terimli, farklı katsayılara sahip olmalarına rağmen aynı değişkenler tarafından oluşturuldukları ve aynı üslere yükseltildikleri için benzerdir.

$4x^5y^3 \qquad \qquad 9x^5y^3$

Daha sonra göreceğimiz gibi, bu tür tek terimliler, tek terimlilerle ilgili işlemleri çözmek için kullanılır.

homojen monomlar

Mutlak dereceleri eşit olduğunda iki monom homojendir .

Örneğin, aşağıdaki iki tek terimli homojendir çünkü her ikisinin de derecesi 5’e eşittir:

$2x^5 \qquad \qquad 6x^2y^3$

Birinci monomiyalin 5’in üssü olan tek bir değişkeni vardır, yani derecesi 5’tir. İkinci polinomun ise bir değişkeni karesi ve diğeri küpü vardır, yani derecesi de 5’tir (2+ 3 =5).

Gördüğünüz gibi, iki tek terimlinin homojen olması için, aynı gerçek parçaya sahip olmaları gerekmez, yalnızca aynı mutlak dereceye sahip olmaları gerekir.

heterojen monomlar

Heterojen monomlar, aynı mutlak dereceye sahip olmayan monomlardır. Başka bir deyişle, heterojen monomlar homojen monomların tam tersidir.

Aşağıdaki 3 monom heterojendir çünkü her birinin derecesi farklıdır:

$x^8 \qquad 3xy \qquad 7a^9b^2$

İlk tek terim 8. dereceden, ikinci tek terim 2. dereceden ve üçüncü tek terim 11. derecedendir. Bu nedenle, üç tek terim birbirine göre heterojendir.

Karşıt monomiyaller

Karşıt monomlar homojen olan (aynı gerçek parçaya sahip) ve ayrıca katsayıları zıt olan, yani katsayıları aynı değere ancak zıt işarete sahip olan monomlardır.

Örneğin, aşağıdaki iki tek terimli birbirine zıttır:

$3x^5y^2 \qquad \qquad -3x^5y^2$

Önceki iki tek terimli zıttır çünkü yalnızca işaretleri farklıdır, birincisi pozitif işarete ve ikincisi negatif işarete sahiptir.

Artık tek terimlilerin birkaç örneğini gördüğünüze göre, başka bir benzer cebirsel ifade ilginizi çekebilir: binom . Aslında bir binom, birkaç tek terimlinin toplanmasından (veya çıkarılmasından) oluşur, dolayısıyla bu iki kavram arasındaki ilişkiyi görmek ilginçtir. Bu bağlantıya tıklayarak binomun ne anlama geldiğini görebilirsiniz.

Tek terimli işlemler

Tek terimli kavramını derinleştirmek için tek terimlilerle hangi işlemlerin yapılabileceğini göreceğiz. Özellikle tek terimli sayılar toplanabilir, çıkarılabilir, çarpılabilir, bölünebilir ve kuvvetlendirilebilir. Ve her operasyonun kendine has özellikleri var, o yüzden aşağıda bunları tek tek inceleyeceğiz.

monomların toplamı

İki veya daha fazla tek terimli yalnızca benzer tek terimli olmaları durumunda toplanabilir. O halde, iki benzer tek terimlinin toplamı, aynı değişmez kısımdan oluşan başka bir tek terimliye ve bu iki tek terimlinin katsayılarının toplamına eşittir.

Tek terimlilerin toplamlarına örnekler

$2x^4+3x^4 = 5x^4$
$4y^2+y^2 = 5y^2$
$7x^3y+2x^3y = 9x^3y$
$2a^3b^2c^6+6a^3b^2c^6 = 8a^3b^2c^6$
$4x^3+2x^3+5x^3=6x^3+5x^3=11x^3$

Tek terimli toplama alıştırmaları yapmak istiyorsanız sağ üstteki arama motorunda arayabilirsiniz çünkü çözülmüş tek terimli toplama alıştırmalarıyla dolu bir sayfamız var.

monomların çıkarılması

İki veya daha fazla tek terimli, yalnızca benzer tek terimli olmaları durumunda çıkarılabilir. Böylece, iki benzer tek terimlinin çıkarılması, aynı değişmez kısımdan oluşan başka bir tek terimliye ve bu iki tek terimlinin katsayılarının çıkarılmasına eşittir.

Tek Terimli Sayıların Çıkarılması Örnekleri

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

Web sitemizde bulabileceğiniz adım adım tek terimli çıkarma işlemlerinin çözümlü alıştırmalarını yapabilirsiniz. Bunları sağ üstteki arama motoru aracılığıyla bulabilirsiniz.

monomların çarpımı

İki monomlunun çarpımı sonucu, katsayısı monomluların katsayılarının çarpımı olan ve gerçek kısmı aynı tabana sahip değişkenlerin çarpılmasıyla, yani katsayılarının eklenmesiyle elde edilen başka bir monomlu elde edilir.

Dolayısıyla iki farklı monomlu sayının çarpımını çözmek için katsayıların birbiriyle çarpılması ve aynı tabana sahip kuvvetlerin üslerinin toplanması gerekir.

Öte yandan, taban kuvvetleri farklı iki tek terimliyi çarparsak, katsayılarını birlikte çarpmamız ve kuvvetlerini aynı bırakmamız gerekir:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Tek terimlilerin çarpımına örnekler

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Tek terimlilerin çarpımı ile ilgili adım adım çözümlü alıştırmalar yapmak için bu sitedeki makaleye başvurabilirsiniz. Sağ üstteki arama motoruyla kolayca bulacaksınız.

monomların bölünmesi

Monomların bölünmesinin sonucu, katsayısı monomların katsayılarının bölümüne eşit olan ve gerçek kısmı aynı tabana sahip değişkenlerin bölünmesiyle, yani katsayılarının çıkarılmasıyla elde edilen başka bir monomdur.

Yani iki farklı tek terimliyi bölmek için katsayıları aralarında böleriz ve aynı tabana sahip kuvvetlerin üslerini çıkarırız.

Tek terimlilerin bölünmesine örnekler

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

Tek terimlileri bölmek göründüğünden daha zordur, bu nedenle tek terimlileri bölmeyle ilgili çözülmüş alıştırmaları adım adım yapmaya çalışmanızı öneririz. Bunları bulmanın en hızlı yolu sağ üstteki arama motorumuzu kullanmaktır.

bir monomialin gücü

Bir monomlunun kuvvetini hesaplamak için, monomlunun her bir elemanının kuvvet üssüne yükseltilmesi gerekir . Başka bir deyişle, bir monomiyalin kuvveti, katsayısını ve değişkenlerini (harflerini) kuvvetin üssüne yükseltmekten ibarettir.

Üslerin özelliklerinden, zaten yükseltilmiş bir terimi yükselttiğimizde iki üssün birlikte çarpıldığını hatırlayın. Bu nedenle bir tek terimlinin kuvvetlerinde her harfin üssü her zaman kuvveti gösteren üs ile çarpılır .

Tek terimlilerin kuvvetlerine örnekler

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Tek terimlilerle yapılan bu tür işlemlerde hata yapmak oldukça kolaydır. Bu yüzden sitemizde adım adım çözdüğümüz alıştırmalarla pratik yapmanızı öneririz. Sağ üstteki arama motorunda arayarak bunları hızlı bir şekilde bulacaksınız.

Tek terimlinin sayısal değeri

Bir monomlunun sayısal değeri, bir monomlunun değişkenlerinin belirli değerlerle değiştirilmesiyle elde edilen sonuçtur.

Örneğin, aşağıdaki monomialimiz varsa:

$5x^2$

Önceki tek terimlinin sayısal değerini bulmak istiyorsak

$x=2$

mektubu değiştirmeniz gerekiyor

$x$

monomialin 2’ye eşitlenmesi ve elde edilen işlemleri çözmesi:

$5\cdot 2^2= 5 \cdot 4 = 20$

Yani monomialin sayısal değeri

$5x^2$

İçin

$x=2$

20’ye eşittir.

Ayrıca tek terimli bir çok değişkenin sayısal değerini de belirleyebilirsiniz. Örneğin, aşağıdaki iki değişkenli veya başka bir deyişle iki değişkenli tek terimliysek:

$3x^4y$

Yukarıdaki monomialin sayısal değerini hesaplamak için

$x$

1 e değerinde

$y$

-2 ise, harfleri ilgili değerlerinin yerine koyarız:

$3\cdot 1^4\cdot (-2)= 3 \cdot 1 \cdot (-2) = -6$

Yani problemin tek terimlisinin sayısal değeri

$x=1$

$y=-2$

-6 değerini döndürür.

Monomiyaller ve polinomlar

Son olarak polinomların tek terimlilerden oluşturulabileceğini bilin:

Bir polinom, iki veya daha fazla monomiyalin gruplandırılmasıdır.

$P(x)= 4x^5+3x^2-7x$

Örneğin, önceki polinom, 3 heterojen monomiyalin toplanmasından (veya çıkarılmasından) kaynaklanır.

Meraktan dolayı, bir polinomun yalnızca 2 tek terimli olması durumunda buna binom denir. Ve bir polinomun tam olarak 3 tek terimli olması durumunda buna üçlü terim denir.

Polinomlar hakkında daha fazla bilgi edinmek istiyorsanız, polinomlar hakkında bilmeniz gereken her şeyi açıkladığımız webin ana sayfasını ziyaret edebilirsiniz.