Matris toplama ve çıkarma işlemi nasıl hesaplanır

Bu sayfada matrislerin nasıl toplanıp çıkarılacağını göreceğiz. Ayrıca mükemmel bir şekilde anlamanıza yardımcı olacak örnekler ve pratik yapabilmeniz için çözülmüş alıştırmalar da var. Ayrıca matris toplama işleminin tüm özelliklerini bulacaksınız.

Matrisler nasıl eklenir ve çıkarılır?

İki matrisin toplamasını (veya çıkarmayı) hesaplamak için matrislerde aynı konumu işgal eden elemanları eklemeniz (veya çıkarmanız) gerekir.

Örnekler:

İki matrisi toplamak veya çıkarmak için aynı boyuta sahip olmaları gerektiğini unutmayın. Örneğin aşağıdaki matrisler eklenemez çünkü birincisi 2×2’lik bir matris, ikincisi ise 3×2’lik bir matristir:

$\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}$

Matrislerde toplama ve çıkarmaya yönelik çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki 2×2 matrislerin toplamını hesaplayın:

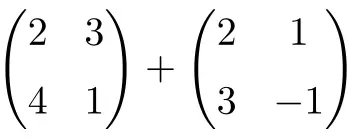
2x2 matrislerin eklenmesi için adım adım çözülen alıştırma

Çözüme bakın

Boyutu 2×2 olan iki kare matrisin toplamıdır:

$\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}$

Alıştırma 2

Aşağıdaki matris çıkarma işlemini gerçekleştirin:

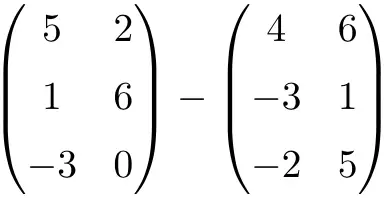
matrislerde adım adım çözülmüş alıştırma, matrislerle işlemler

Çözüme bakın

Bu, boyutları 3×2 olan iki matrisin çıkarılmasıdır:

$\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}$

Alıştırma 3

Aşağıdaki 3×3 boyutunun matris toplamının sonucunu bulun:

Çözüme bakın

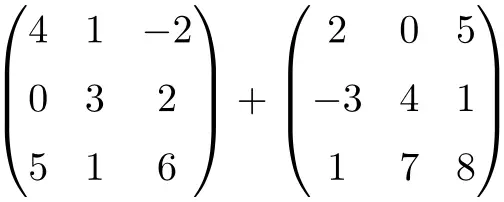
3×3 düzeyindeki iki kare matrisin toplamıdır:

$\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}$

Alıştırma 4

2. mertebeden kare matrislerin aşağıdaki toplama ve çıkarma işlemlerini hesaplayın:

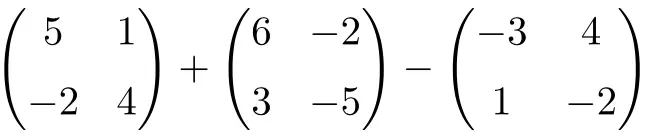
alıştırma 2x2 matrislerde adım adım toplama ve çıkarma, matrislerle işlemler çözüldü

Çözüme bakın

Bu, 2. dereceden kare matrislerin toplanması ve çıkarılmasıyla birleştirilmiş bir işlemdir:

$\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}$

İlk önce soldaki matrisleri ekliyoruz:

$\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}$

Daha sonra matrislerin çıkarılmasını hesaplıyoruz:

$\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}$

Alıştırma 5

Aşağıdaki matris toplama ve çıkarma işlemlerini çözün:

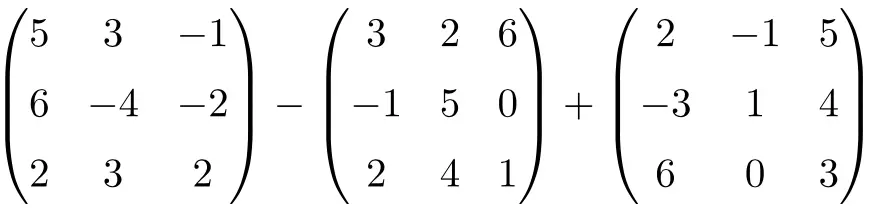
alıştırma 3x3 matrislerde adım adım toplama ve çıkarma, matrislerle işlemler çözüldü

Çözüme bakın

Bu, 3. dereceden kare matrislerin çıkarılması ve eklenmesinden oluşan birleşik bir işlemdir:

$\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}$

İlk olarak matris çıkarma işlemini çözüyoruz:

$\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}$

Ve son olarak matrisleri ekliyoruz:

$\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}$

Artık matrisleri nasıl toplayıp çıkaracağınızı bildiğinize göre, matris işlemlerinin kesinlikle en önemlisi olan matrisleri nasıl çarpacağınızı görmenin tam zamanı. Ayrıca bu sitenin tüm sayfalarında olduğu gibi pratik yapabilmeniz için adım adım çözülmüş matris çarpım alıştırmaları da bulacaksınız. 😉

Matris Özellikleri Ekle

Matris ekleme aşağıdaki özelliklere sahiptir:

Matris toplamanın değişme özelliği vardır:

$\displaystyle A +B = B + A$

Bu nedenle matrisleri toplama sırası aynıdır. Bunu göstermek için iki matrisin sırasını değiştirerek toplayacağız ve sonucun nasıl aynı olduğunu göreceksiniz.

Bu nedenle iki matrisi belirli bir sırayla toplamaya devam ediyoruz:

$\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}$

Matrislerin toplama sırasını tersine çevirirsek sonucun aynı kalacağını unutmayın:

$\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}$

Matris toplamanın bir başka özelliği de karşıt elemanın özelliğidir:

$\displaystyle A + (-A) =0$

Başka bir deyişle, bir matris artı aynı matrisi toplarsak ancak tüm elemanları işaretlerini değiştirirsek sonuç bir sıfır matrisi olacaktır:

$\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}$

Matris toplama aynı zamanda nötr eleman özelliğine de sahiptir:

$\displaystyle A + 0 =A$

Bu özellik en belirgin olanıdır; herhangi bir matris artı sıfırlarla dolu bir matrisin aynı matrise eşdeğer olduğu gerçeğini ifade eder:

$\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}$

Matris toplamanın ilişkisel özelliği vardır:

$\displaystyle\left( A + B \right) + C =A + \left( B + C \right)$

Bu nedenle matrisleri toplama sırası aynıdır. Farklı sıralarla 3 matrisi topladığımız ve sonucun aynı olduğu aşağıdaki örneğe bakın:

$\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}$

$\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}$

$\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}$

Matrisler nasıl eklenir ve çıkarılır?

Örnekler:

Matrislerde toplama ve çıkarmaya yönelik çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Matris Özellikleri Ekle

Yorum bırakın Yanıtı iptal et