▷ Kotanjantın türevi (formül ve örnekler)

Bu yazıda bir fonksiyonun kotanjantının nasıl türetileceğini göreceğiz. Kotanjantın türevine ilişkin örnekler ve hatta adım adım çözülen alıştırmalar bulacaksınız. Son olarak kotanjantın türevinin formülünü kanıtlıyoruz.

Kotanjantın türevinin formülü

X’in kotanjantının türevi, negatif bir bölü x’in sinüsünün karesine eşittir. X’in kotanjantının türevi de eksi x’in kosekantının karesi ve eksi birin toplamı artı x’in kotanjantının karesine eşittir.

$\begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}$

Argüman kotanjantı x dışında bir fonksiyon ise, bir fonksiyonun kotanjantının türevine ilişkin formüller öncekilerle aynıdır, ancak ifadeler argümanın fonksiyonunun türevi ile çarpılır.

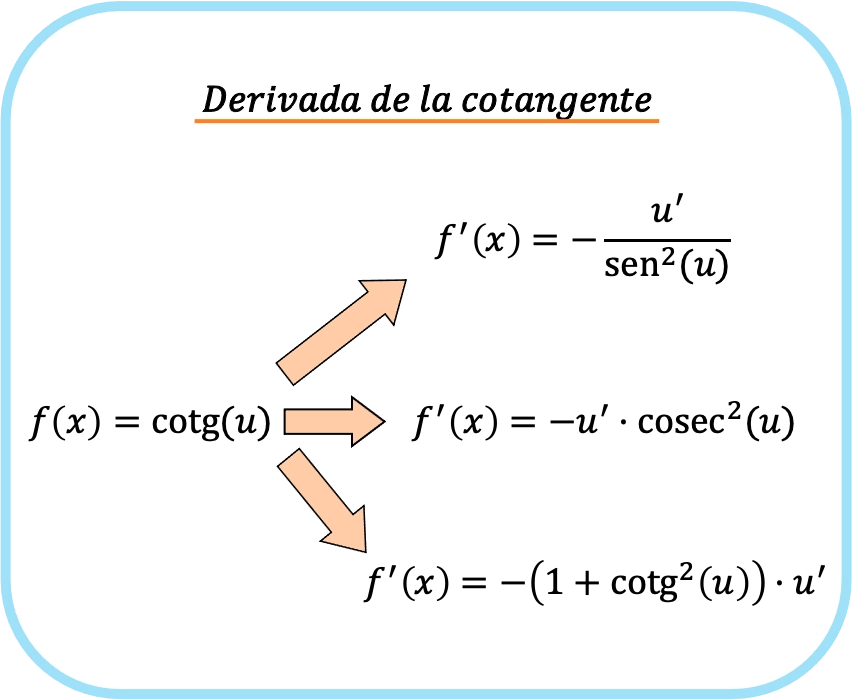
$\begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}$

Bu, kotanjantın türevini bulmak için üç farklı formül olduğu anlamına gelir. Ancak mantıksal olarak her üç formülün de kullanılmasına gerek yoktur, ancak tercih ettiğiniz formülle türetebilirsiniz.

Kotanjantın türevine örnekler

Artık bir fonksiyonun kotanjantının türevinin formülünü gördüğümüze göre, bu bölümde bu tür trigonometrik türevlerin birkaç örneğini çözeceğiz.

Örnek 1: 2x kotanjantının türevi

Bu örnekte 2x fonksiyonunun kotanjantının türevinin ne olduğunu göreceğiz.

$f(x)=\text{cotg}(2x)$

Gördüğümüz gibi kotanjantın türevini hesaplamak için yukarıda görülen üç formülden birini kullanabilirsiniz. Bu durumda sinüzoidal formülü kullanacağız:

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

2x birinci dereceden bir terim olduğundan türevi 2’dir. Yani 2x’in kotanjantının türevi negatif iki bölü 2x’in sinüsünün karesidir:

$f(x)=\text{cotg}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\text{sen}^2(2x)}$

Örnek 2: x karenin kotanjantının türevi

İkinci örnekte x karenin kotanjantının türevinin ne olduğunu belirleyeceğiz.

$f(x)=\text{cotg}(x^2)$

Bu örnekte kotanjant argümanının işlevi bir x değildir, dolayısıyla kotanjantın türevini almak için zincir kuralını uygulamamız gerekir.

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

x karenin türevi 2x olduğundan x ^2’nin kotanjantının türevi:

$f(x)=\text{cotg}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\text{sen}^2(x^2)}$

Örnek 3: Kotanjant küpünün türevi

Son olarak bir polinom fonksiyonunun kübik kotanjantının türevinin ne kadar olduğunu bulacağız:

$f(x)=\text{cotg}^3(x^5-6x^2+10)$

Bu durumda elimizde bir fonksiyonlar bileşimi var, dolayısıyla kotanjantın türevini bulmak için bir kuvvetin türevi formülüyle birlikte zincir kuralını kullanmamız gerekiyor:

$\displaystyle f'(x)=-3\cdot\text{cotg}^2(x^5-6x^2+10)\cdot\frac{5x^4-12x}{\text{sen}^2(x^5-6x^2+10)}$

Kotanjantın türevine ilişkin çözülmüş alıştırmalar

Aşağıdaki kotanjant fonksiyonların türevini hesaplayın:

$\text{A) } f(x)=\text{cotg}(5x)$

$\text{B) } f(x)=\text{cotg}(2x^4+10x-3)$

$\text{C) } \displaystyle f(x)=\text{cotg}^5\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{cotg}\left(e^{x^2}\right)$

$\text{E) } f(x)=\text{cotg}\bigl(\ln(x^2)\bigr)$

$\text{F) } f(x)=\text{cotg}\left(\sqrt{8x}\right)$

Çözümü görün

$\text{A) } f'(x)=-\cfrac{5}{\text{sen}^2(5x)}$

$\text{B) } f'(x)=-\cfrac{8x+10}{\text{sen}^2(2x^4+10x-3)}$

$\text{C) } \displaystyle f'(x)=5\cdot \text{cotg}^4\left(\frac{x}{2}\right)\cdot \left(-\frac{1}{\text{sen}^2\left(\frac{x}{2}\right)}\right)\cdot \frac{1}{2}=-\frac{5\cdot \text{cotg}^4\left(\frac{x}{2}\right)}{2\cdot \text{sen}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=-\cfrac{2x\cdot e^{x^2}}{\text{sen}^2(e^{x^2})}$

$\text{E) } f'(x)=-\cfrac{\cfrac{2x}{x^2}}{\text{sen}^2\bigl(\ln(x^2)\bigr)}=-\cfrac{2}{x\cdot\text{sen}^2\bigl(\ln(x^2)\bigr)}$

$\text{F) } f'(x)=-\cfrac{\frac{8}{2\sqrt{8x}}}{\text{sen}^2\left(\sqrt{8x}\right)}=-\cfrac{4}{\sqrt{8x}\cdot \text{sen}^2\left(\sqrt{8x}\right)}$

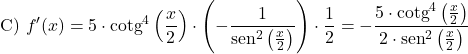
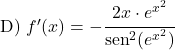
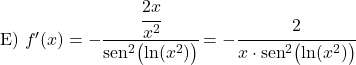
Kotanjantın türevinin kanıtı

Bu son bölümde kotanjantın türevinin formülünü göstereceğiz. Bunu yapmak için, kosinüs bölü sinüse eşit olan kotanjant fonksiyonunun matematiksel tanımından başlayacağız:

$\text{cotg}(x)=\cfrac{\text{cos}(x)}{\text{sen}(x)}$

Şimdi bir bölümün türevi kuralını uygulayarak fonksiyonun türevini alıyoruz;

$\displaystyle\bigl(\text{cotg}(x)\bigr)'=\left(\frac{\text{cos}(x)}{\text{sen}(x)}\right)'$

$\text{cotg}'(x)=\cfrac{-\text{sen}(x)\cdot \text{sen}(x)-\text{cos}(x)\cdot \text{cos}(x) }{\text{sen}^2(x)}$

$\text{cotg}'(x)=\cfrac{-\text{sen}^2(x)-\text{cos}^2(x)}{\text{sen}^2(x)}$

Paydadaki ortak faktörü alıyoruz ve kesirdeki eksi işaretini kaldırıyoruz:

$\text{cotg}'(x)=\cfrac{-\bigl(\text{sen}^2(x)+\text{cos}^2(x)\bigr)}{\text{sen}^2(x)}$

$\text{cotg}'(x)=-\cfrac{\text{sen}^2(x)+\text{cos}^2(x)}{\text{sen}^2(x)}$

Öte yandan temel trigonometrik özdeşlik sayesinde sinüsün karesi artı kosinüsün karesinin bire eşit olduğunu biliyoruz.

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{cotg}'(x)=-\cfrac{1}{\text{sen}^2(x)}$

Ve böylece kotanjantın türevinin ilk formülünü elde ettik. Benzer şekilde, kosekant sinüsün çarpımsal tersidir, dolayısıyla kotanjantın türevinin ikinci kuralı da kanıtlanmış olur:

$\text{cotg}'(x)=-\text{sec}^2(x)$

Son olarak, bu trigonometrik fonksiyonun türevinin üçüncü formülü, önceki adımdaki kesirin kesirlerin toplamına dönüştürülmesiyle kanıtlanabilir: