Bu sayfada konik kesitlerin tanımını, neden bu kadar önemli olduklarını ve var olan farklı konik kesit türlerini (daire, elips, hiperbol ve parabol) bulacaksınız. Ayrıca denklemleri arasındaki farkları da görebileceksiniz.
Konik bölümler nelerdir?
Analitik geometride, konik bölümler (veya basitçe konikler), bir koni ile bir düzlem arasındaki farklı kesişimlerden kaynaklanan, bu düzlem koninin tepe noktasından geçmediğinde ortaya çıkan tüm eğrilerdir. Dört tür konik bölüm vardır: daire, elips, parabol ve hiperbol.
Aşağıda herhangi bir koniden elde edilebilecek 4 olası bölüm verilmiştir:
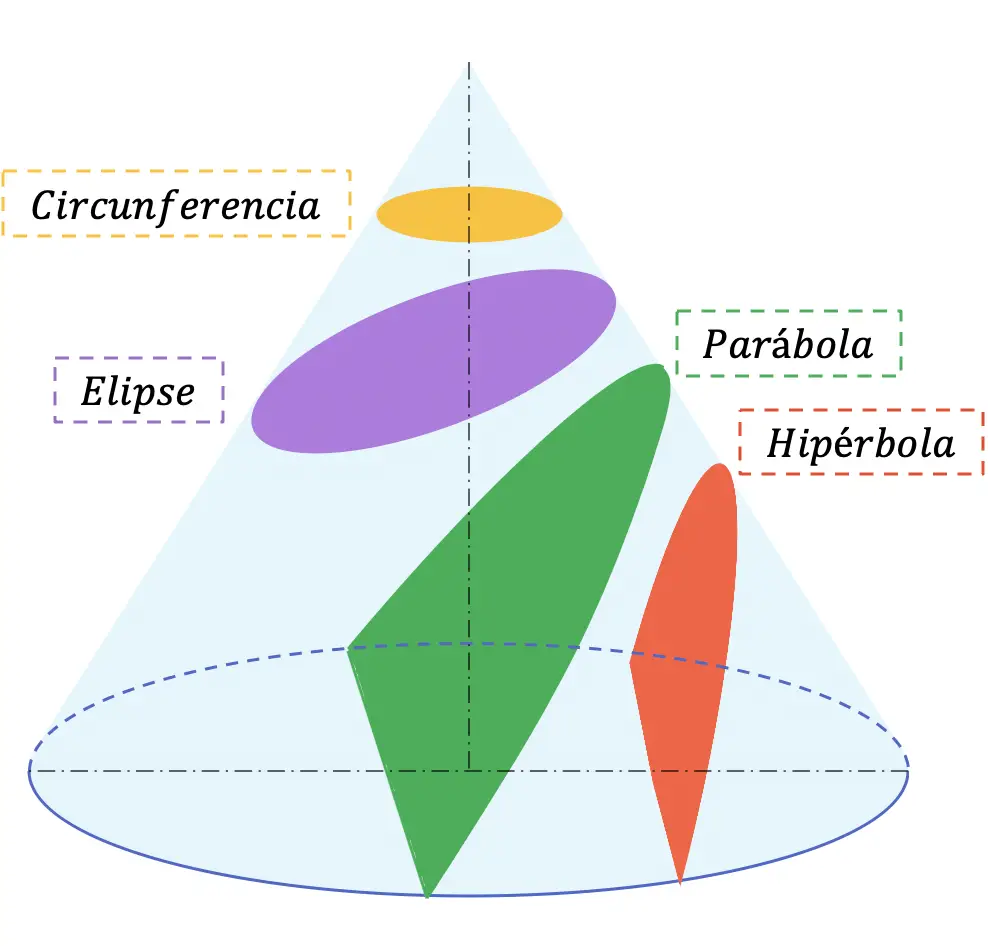
Konik kesitler genellikle ortaokulda (Bachillerato) matematik ve teknik resim derslerinde işlenir.
Konik bölüm türleri
Konik bölüm kavramını gördükten sonra, dört tip konik bölümün ne olduğuna bakalım: daire, elips, parabol ve hiperbol.
çevre
Çevre, dönme eksenine dik (tabana paralel) bir düzleme sahip bir koninin kesilmesiyle bulunabilen konik bir bölümdür.

Ayrıca çevre, düzlem üzerinde merkez adı verilen sabit bir noktadan eşit uzaklıktaki noktaların geometrik yeridir.
Elips
Elips, çevreye çok benzeyen düz, kapalı, kavisli bir çizgidir ancak şekli daha ovaldir. Özellikle, bir koninin yüzeyinin, dönme eksenine göre açısı jeneratörünkinden daha büyük olan eğik bir düzlem tarafından kesilmesinden kaynaklanır.
Ek olarak, bir elipsin tüm noktaları bir koşulu karşılar: elips, bir düzlemin diğer iki sabit noktaya (F ve F’ odakları olarak adlandırılan) uzaklıklarının toplamı sabit olan tüm noktalarının geometrik yeridir.

benzetme
Matematikte parabol, düzlem üzerinde sabit bir noktadan (odak adı verilen) ve sabit bir çizgiden (doğrultman adı verilen) eşit uzaklıkta olan noktaların yeridir.

Geometrik olarak parabol, bir koninin, koninin generatrix açısına eşdeğer dönme eksenine göre eğim açısına sahip bir düzlem tarafından bölümünün sonucudur. Bu nedenle parabolün bulunduğu düzlem koninin üretecine paraleldir.
Bu konik bölümün çok önemli bir özelliği parabol denklemidir , çünkü durumuna bağlı olarak ne tür bir parabol olduğunu belirlememize olanak tanır. Bu bağlantıda parabolün tüm denklemlerini, parabolün elemanlarının neler olduğunu, özelliklerini, örneklerini, çözülmüş alıştırmaları ve parabollerin diğer özelliklerini bulacaksınız.
Hiperbol
Konik bir kesit olarak, bir koni, koninin üretecinin dönme eksenine göre oluşturduğu açıdan daha küçük bir açıyla bir düzlem tarafından kesildiğinde bir hiperbol elde edilir.
Matematiksel olarak bir hiperbol, düzlem üzerinde aşağıdaki özelliği karşılayan noktaların yeri olarak tanımlanabilir: hiperbol üzerindeki herhangi bir nokta ile iki sabit nokta (odak adı verilen) arasındaki mesafeler arasındaki farkın mutlak değeri sabit olmalıdır.
Ayrıca bu iki mesafenin çıkarılmasının değeri her zaman hiperbolün iki köşesi arasındaki mesafeye eşdeğerdir.
![]()

Eminim zaten çıkarmışsınızdır, parametre değeri
![]()
Bir hiperbolün yapısı hiperboller için temeldir. Aşağıdaki bağlantıda hiperbolün neden bu kadar önemli bir katsayı olduğunu ve bir hiperbolü karakterize eden tüm unsurların neler olduğunu bulacağınız hiperbolle ilgili açıklamamızı görebilirsiniz. Ayrıca, bir hiperbol denkleminin neye benzediğini, mevcut farklı hiperbol türlerini ve hatta hiperbollerle ilgili adım adım problemleri ve alıştırmaları bulacaksınız.
Konik bölümlerin genel denklemi
Her konik bölüm analitik olarak bir denklem olarak ifade edilebilir. Aslında tüm konik denklemler ikinci dereceden olmalıdır:
![]()
Sonuç olarak, katsayılardan en az biri
![]()
herhangi biri
![]()
formülün sıfırdan farklı olması gerekir.
Böylece, parametre değerlerine bağlı olarak denklem bir tür koniye veya diğerine karşılık gelecektir:
- Çevre : bir çevreyi tanımlayan genel denklem için terimler

Ve

eşleşmeli ve

sıfır olmalıdır.
![]()
- Elips : Aşağıdaki koşul doğrulandığında denklem bir elipsin matematiksel ifadesine karşılık gelecektir:
![]()
- Parabol : Denklemin parabol olabilmesi için aşağıdaki eşitliğin sağlanması gerekir:
![]()
- Hiperbol : Son olarak, bir hiperbolün genel denklemi aşağıdaki eşitsizliği karşılamalıdır:
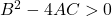 Yazı gezinmesi
Yazı gezinmesi