▷ Kombinatoryal sayı nedir ve nasıl hesaplanır (örnekler)

Bu sayfada kombinatoryal sayının ne olduğunu ve nasıl hesaplandığını (formül) açıklıyoruz. Ayrıca herhangi bir kombinatoryal sayının nasıl hesaplanacağına dair örnekleri görebileceksiniz ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz. Ayrıca kombinatoryal sayıların tüm özelliklerini ve uygulamalarını da gösteriyoruz. Son olarak, bir kombinatoryal sayının sonucunu doğrudan hesap makinesiyle nasıl bulacağımızı öğreniyoruz.

Kombinatoryal sayı nedir?

Matematikte, binom katsayısı olarak da adlandırılan kombinatoryal sayı , n elemanlı bir diziden (n>k) oluşturulabilen k elemanlı grupların sıradan kombinasyonlarının (tekrarsız kombinasyonlar) sayısıdır.

Bir kombinatoryal sayı parantez içinde aşağıdaki şekilde ifade edilir:

$\begin{pmatrix}n \\ k \end{pmatrix}$

Öte yandan, kombinatoryal sayı n / k olarak okunur. Benzer şekilde n’ye pay, k’ya da sıra denir.

Kombinatoryal sayının tanımı ile anlamını anlamak zordur. Ancak şimdi kombinatoryal sayının matematiksel olarak nasıl belirlendiğini göreceğiz ve ardından bu kombinatorik kavramını daha derinlemesine inceleyeceğiz. Göreceksiniz ki bu şekilde daha iyi anlayacaksınız.

Kombinatoryal sayı formülü

Bir kombinatoryal sayının (veya binom katsayısının) değerini hesaplamak için formül aşağıdaki gibidir:

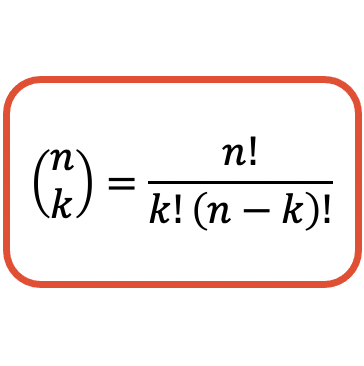
Cebirde ünlem işaretinin bir sayının faktöriyeline karşılık geldiğini unutmayın. Bir sayının faktöriyelini bulmak için 1’in tüm pozitif tam sayılarını o sayıyla çarpmanız gerekir. Örneğin 4 sayısının faktöriyelini hesaplamak için 1, 2, 3 ve 4’ü çarpmanız gerekir:

$4! = 1\cdot 2 \cdot 3 \cdot 4 =24$

0’ın faktöriyelinin 1’e eşit olduğunu bilmeniz de önemlidir.

$0! = 1$

Kombinatoryal sayının hesaplanmasına örnek

Daha sonra örnek olarak bir kombinatoryal sayının değerini adım adım belirleyeceğiz, böylece bunun nasıl yapıldığını görebilirsiniz:

5/3 kombinatoryal sayısının değerini hesaplayın.

5 bölü 3’ün binom katsayısı aşağıdaki ifadeye karşılık gelir:

$\begin{pmatrix}5 \\ 3 \end{pmatrix}$

Bu nedenle, formülü kombinatoryal sayılara uygularsak değerini belirlemek için aşağıdaki işlemleri yapmamız gerekir:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}$

Veya eşdeğer:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}$

Bu nedenle faktöriyelleri buluyoruz:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}$

Çarpma 1·2·3 pay ve paydada tekrarlanır, böylece kesir bu faktörü ortadan kaldırarak basitleştirilebilir:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}$

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}$

Şimdi ürünleri hesaplıyoruz:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}$

Ve son olarak bölmeyi yapıyoruz:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}$

Kombinatoryal sayının özellikleri

Kombinatoryal sayılar veya binom katsayıları aşağıdaki özelliklere göre birleştirilebilir:

İki tamamlayıcı kombinatoryal sayı, aynı n payına sahip olan ve sıralarının toplamı söz konusu paya eşdeğer olan sayılardır. Dolayısıyla iki tamamlayıcı kombinatoryal sayının sonucu aynıdır.

$\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}$

Kombinatoryal sayıların bu özelliğine simetri özdeşliği de denir.

Örneğin 6 bölü 4, 6 bölü 2 ile aynı sonucu verir çünkü 6-4=2.

$\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}$

$\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}$

Payı ve ardışık sıraları aynı olan iki kombinatoryal sayının toplamı, payı toplamaların payı artı 1’e eşit olan ve sırası toplamaların mertebelerinin en büyük değerine karşılık gelen başka bir kombinatoryal sayıya eşittir. Başka bir deyişle, aşağıdaki koşul her zaman karşılanır:

$\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}$

Örneğin:

$\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}$

Bu özelliğe Pascal kuralı da denir.

Öte yandan, bu formül aynı zamanda bir kombinatoryal sayıyı iki daha basit kombinatoryal sayıya ayrıştırmak için tersten de uygulanabilir:

$\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}$

Örneğin, 8 bölü 4 kombinatoryal sayısı, 7 bölü 3 artı 7 bölü 4’e eşittir:

$\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}$

1’den büyük herhangi bir pozitif sayı, sayının kendisine eşittir.

$\begin{pmatrix}n\\ 1 \end{pmatrix} =n$

Bu özelliğin nedeni, bir sayının faktöriyelinin önceki sayının faktöriyelinin sayının kendisi ile çarpımına eşit olmasıdır:

$\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n$

Bu tür kombinatoryal sayıların örnekleri:

$\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9$

0’dan büyük her pozitif sayı bire eşittir.

$\begin{pmatrix}n\\ 0 \end{pmatrix} =1$

Aslında böyle bir kombinatoryal sayının kesirinin paydası her zaman kesrin payına eşit olacaktır:

$\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1$

Bunun gibi kombinatoryal sayılara örnekler:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1$

Her sayı kendi başına 1’e eşittir.

$\begin{pmatrix}n\\ n \end{pmatrix} =1$

İşte demo:

$\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1$

Bunun gibi kombinatoryal sayılara örnekler:

$\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1$

Hesap makinesiyle kombinatoryal sayı nasıl hesaplanır

Şu ana kadar az ya da çok basit sayıların birleşimsel sayısını nasıl bulacağımızı gördük, ancak çok büyük miktarlarla işlem yapmamız gerektiğinde, birleşimsel sayıyı belirlemek için hesap makinesini kullanmak daha iyidir. Şimdi hesap makinesine bir kombinatoryal sayının nasıl girileceğini göreceğiz.

Yani hesap makinesiyle bir kombinatoryal sayıyı hesaplamak için kullanılan anahtar nCr anahtarıdır . Kombinatoryal sayının değerini belirlemek için ise öncelikle kombinatoryal sayının payını girmeniz, ardından nCr tuşuna basmanız, ardından kombinatoryal sayının sırasını girmeniz ve son olarak eşittir tuşuna basmanız gerekir.

$\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}$

CASIO bilimsel hesap makinelerinde, modele bağlı olarak nCr tuşunun genellikle kendi düğmesi vardır veya bölme düğmesinin üzerinde bulunur.

Örneğin, 10 bölü 6’nın kombinatoryal sayısının ne olduğunu bilmek istiyorsak aşağıdaki sırayı yapmalıyız:

$\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210$

Kombinatoryal sayının uygulamaları

Eğer bu noktaya kadar geldiyseniz, muhtemelen herhangi bir kombinatoryal sayıyı nasıl çözeceğinizi zaten biliyorsunuzdur, mükemmel. Ama… kombinatoryal sayı ne için kullanılıyor? O zaman bu tür çok özel bir operasyonun sunduğu tüm avantajları göreceğiz.

Kombinatorik

Sayfanın üst kısmında gördüğümüz gibi bir kombinatoryal sayının sonucu

$\begin{pmatrix}n\\ k \end{pmatrix}$

olası grup sayısını temsil eder

$k$

toplam bir diziden oluşturulabilen elemanlar

$n$

öğeler.

Bu nedenle, bazı kombinatoryal problemler kombinatoryal sayılar (veya binom katsayıları) kullanılarak çözülebilir. Bir örnek kullanarak bunun nasıl yapılacağını görelim:

30 kişilik bir sınıfta belirli görevleri yerine getirmek üzere 4 kişilik bir grup seçmek istiyoruz. Oluşturulabilecek toplam farklı grup sayısı nedir?

Bu durumda öğrencilerin sırasının bir önemi yoktur, aynı öğrenci grup içinde iki kez tekrarlanmaz ve tüm öğrenciler gruba girmez. Bu nedenle grubun kaç farklı şekilde oluşturulabileceğini belirlemek için kombinatoryal sayı formülü kullanılabilir.

Bunun için pay olarak toplam öğrenci sayısını, grubu oluşturacak öğrenci sayısını da sıralayarak kombinatoryal sayıyı hesaplamanız gerekir:

$\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}$

Dolayısıyla olası kombinasyonların toplam sayısı 27.405 gruptur.

Newton’un iki terimlisi

Kombinatoryal sayıların bir başka uygulaması da Newton binomudur. Newton’un binom’u, birlikte bir tamsayıya yükseltilen iki terimden oluşan bir polinomdur; yani Newton’un binomunun, aşağıdaki cebirsel ifadeye yanıt veren polinom olduğu anlamına gelir:

$(a+b)^n$

Açıkçası, eğer binomun karesi alınırsa, bu onun dikkate değer bir özdeşlik olduğu anlamına gelir ve dolayısıyla karşılık gelen formülle kolayca hesaplanabilir. Öte yandan binom büyük sayılara yükseltildiğinde hesaplama oldukça zorlaşır. Newton’un binom teoremi, bu tür polinomların kombinatoryal sayılardan çok kolay hesaplanabileceğini söylüyor.

Aşağıdaki bağlantıya tıklayın ve Newton’un binom formülünün ne olduğunu ve nasıl hesaplandığını öğrenin. Ayrıca örnekleri görebilecek ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz. Ve son olarak bu teoremin ilginç geçmişini keşfedeceksiniz.

Tartaglia’nın (veya Pascal’ın) üçgeni

Bu makale boyunca gördüğünüz gibi, büyük sayıların binom katsayısını manuel olarak hesaplamak zahmetli ve karmaşık olabilir.

Öte yandan Pascal üçgeni olarak da adlandırılan Tartaglia üçgeninde tüm kombinatoryal sayılar anımsatıcı bir kural kullanılarak kolayca belirlenebilir. Bu mantıksal olarak çok faydalıdır çünkü hesaplamalar sırasında çok fazla zaman tasarrufu sağlar.

Bunun tam olarak nasıl yapılacağını öğrenmek için Tartaglia’nın üçgen açıklamasına bakın. Bu bağlantılı sayfada, bu gizemli üçgenin ne olduğunu, ne için kullanıldığını (şaşırtıcı uygulamaları var) 😮 ve kökeninin ne olduğunu (zaten 1000 yıldan daha önce kullanılıyordu) öğreneceksiniz.

Çözülmüş kombinatoryal sayı alıştırmaları

Açıklanan kavramları uygulayabilmeniz ve tam olarak anlayabilmeniz için, size kombinatoryal sayılarla ilgili adım adım çözülmüş birkaç alıştırma bırakıyoruz.

1. Egzersiz

9’a 5’lik kombinatoryal sayıyı bulun (hesap makinesi kullanmadan).

Çözümü görün

5 üzerinden 9 olan kombinatoryal sayının değerini bulmak için basitçe faktöriyel formülü uygularız:

$\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}$

Alıştırma 2

Aşağıdaki iki kombinatoryal sayının toplamının sonucu nedir? (hesap makinesi olmadan)

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}$

Çözümü görün

Kombinatoryal sayıların özelliklerinden problemin toplamının aşağıdaki kombinatoryal sayıya eşit olduğu sonucu çıkar:

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}$

Bu nedenle, 7 üzerinden 11’lik kombinatoryal sayıyı hesaplamak yeterlidir:

$\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}$

Alıştırma 3

Aşağıdaki kombinatoryal sayıların eşit olup olmadığını belirleyin:

$\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}$

Çözümü görün

Üç kombinatoryal sayının sonucunu bulmak için hesap makinesi kullanmanıza gerek yoktur ancak kombinatoryal sayıların özellikleri sayesinde kolayca bulunabilirler.

Öncelikle 0’dan büyük herhangi bir sayının kombinatoryal sayısı 1’i verir. Dolayısıyla:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1$

Öte yandan birden büyük her sayı o sayının kendisine eşittir. Henüz:

$\begin{pmatrix}6\\ 1 \end{pmatrix} =6$

Ve son olarak, aynı sayının iki kez tekrarlanmasıyla oluşturulan herhangi bir kombinatoryal sayı 1’e eşdeğerdir. Yani:

$\begin{pmatrix}6\\ 6 \end{pmatrix} =1$

Sonuç olarak problemdeki birinci ve üçüncü birleşimsel sayılar eşit ancak ortadaki birleşimsel sayıdan farklıdır.

$\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}$

Kombinatoryal sayı (veya binom katsayısı)