Kimlik veya matris birimi

Bu sayfada Kimlik (veya Birim) matrisinin ne olduğunu ve çeşitli örnekleri göreceksiniz. Ayrıca birim matrisin özelliklerinin neler olduğunu, bu tür matrislerle nasıl çalışılacağını ve determinantının sonucunun ne olduğunu açıklıyoruz. Son olarak bu çok özel matrisin sahip olduğu uygulamaları bulacaksınız.

Kimlik matrisi nedir?

Kimlik (veya Birim) matrisi, tüm elemanların bir (1) olduğu ana köşegen dışında sıfırlarla (0) dolu bir kare matristir.

Bu, birim matrisin veya birlik matrisinin tanımıdır, ancak bunu örnekler aracılığıyla mutlaka daha net göreceksiniz:

Kimlik matrislerine örnekler

2 × 2 boyutunun birim matris örneği

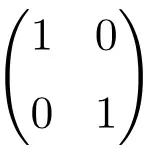
2x2 boyutunda benzersiz kimlik veya matris

3×3 sıralı Kimlik matrisi örneği

3x3 boyutunda kimlik veya benzersiz matris

4×4 boyutunda Kimlik matrisi örneği

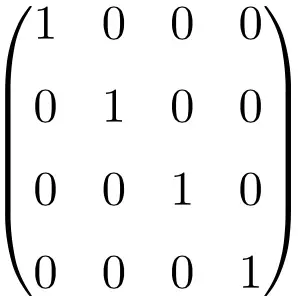
4x4 boyutunun kimliği veya benzersiz matrisi

Gördüğünüz gibi, birim matrisi oluşturmak için hala aynı prosedürü izlememiz gerekiyor: birleri (1) ana köşegen üzerine ve geri kalanların hepsini sıfır (0) koyun. Değişen tek şey masanın boyutudur.

Kimlik tablosu özellikleri

Kimlik matrisi, birim matris ve hatta özdeş matris matematikte yaygın olarak kullanılmaktadır ve bu, bu tür matrisin sahip olduğu özelliklerden kaynaklanmaktadır:

Kimlik matrisi köşegen matrisin bir örneğidir.

Üniter bir matris hem üst hem de alt üçgen matristir .

Kimlik matrisi aynı zamanda simetrik bir matristir .

Kimlik matrisinin vekili kendisidir.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Tersine çevrilebilir bir matristir. Ve eke gelince, Birim matrisinin tersi kendisidir:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Herhangi bir skaler matris, bir sayının birim matrisle çarpılmasından elde edilebilir:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Özdeş matrisin tüm özdeğerleri (veya özdeğerleri) 1’dir:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Son olarak birim matris aynı zamanda permütasyon matrisinin bir örneğidir.

Kimlik (veya Birim) matrisiyle işlemler

Muhtemelen şunu düşünüyorsunuz: Bütün bunlar çok iyi ama… ve Kimlik matrisi ne işe yarar? Keşke 0’lar ve 1’lerden oluşan bir tablo olsaydı!

Henüz bu konuyu vermemiş olsanız da birim matris matematikte çok kullanılır, aslında bu tür kare matrisler lineer cebirde çok önemlidir. Kimlik matrisinin temel faydası, matris işlemlerinin hesaplanmasına olanak sağlaması kolaylığıdır. Şimdi Kimlik matrisiyle nasıl çalışılacağını görelim:

Kimlik Matrisi ile Toplama ve Çıkarma İşlemleri

Bir matrisin ana köşegenine diğer elemanları değiştirmeden sayılar eklemenin (veya çıkarmanın) bir yolu birim matrisi kullanmaktır çünkü bu sayılara yalnızca bir birim ekler (veya çıkarır). elementler:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

Ayrıca, önce birim matrisi bir skalerle çarparak köşegen üzerindeki öğelere daha fazla birim ekleyebilir veya çıkarabilirsiniz:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Bir matrisin birim matrisle çarpımı

Bir matris birim matris ile çarpıldığında nötr bir eleman gibi davranır, yani herhangi bir matris birim matrisle çarpıldığında aynı matris elde edilir. Aşağıdaki örneğe bir göz atın:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Ayrıca matris çarpımının anlamının da bir önemi yoktur, yani birim matrisi sağla veya solla çarpmamızın bir önemi yoktur çünkü sonuç her zaman aynı matris olacaktır. Bunu göstermek için önceki alıştırmayı tekrarlıyoruz ancak bu sefer Özdeşlik matrisini karşı tarafla çarpıyoruz:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Kimlik matrisinin gücü

Birim matrisinin gücü, matrisi yükselttiğimiz üs ve matrisin boyutundan bağımsız olarak her zaman birim matrisle sonuçlanır.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Kimlik matrisinin determinantı

Zaten hayal ettiğinizi varsaydığım gibi, Kimlik (veya Birim) matrisinin determinantı, matrisin boyutundan bağımsız olarak her zaman 1’e eşittir .

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Kimlik Matrisi Uygulamaları

Son olarak, tüm bu bilgilerden sonra, birim matrisin neden bu kadar önemli olduğu şeklindeki tipik soruyu nasıl yanıtlayacağınızı muhtemelen zaten biliyorsunuzdur. Rahat olun, bu soruyu daha önce ben de kendime sordum. 😂

Fark etmiş olacağınız gibi birim matrisin birçok kullanımı vardır ve bu yüzden bu kadar ilginçtir. Birim matrisinin kullanım alanlarından biri de işlemlerdir çünkü gördüğümüz gibi onunla matris işlemlerini gerçekleştirmek çok kolaydır.

Öte yandan birim matris, matris denklemlerini çözmek için de kullanılır. Bunu yapmak için aşağıdaki ters matris özelliğini kullanıyoruz: bir matrisi ters matrisiyle çarpmak birim matrise eşittir. Bağlantıya tıklayarak matrislerle bir denklemin nasıl çözüleceğini görebilirsiniz.

Ek olarak birim matris, Gauss yöntemiyle ters matrisin hesaplanmasında da kullanılır. Bu yöntem, birim matrisin yanına bir matris yerleştirilerek daha büyük bir matris oluşturulmasını içerir. Daha sonra orijinal matrisin satırlara elemanter işlemler uygulanarak birim matrise dönüştürülmesi gerekir. Çok karmaşık görünüyor ama gerçekte o kadar da değil, ancak bütün bir prosedürün uygulanması gerekiyor, bu yüzden daha fazla ilgileniyorsanız, web sayfasının arama motorunda bir matrisin nasıl ters çevrileceğini arayabilirsiniz (yukarıdan SAĞA).

Son olarak, Kimlik matrisi aynı zamanda bir matrisin köşegenleştirilmesi ve özdeğerlerinin (veya özdeğerlerinin) hesaplanması için de kullanışlıdır. Çünkü birim matrisin devreye girdiği bazı işlemler sayesinde özdeğerlerin elde edildiği karakteristik polinom elde edilebilmektedir. Ancak bu zaten oldukça ileri düzeyde bir konudur, bu nedenle matris köşegenleştirmeye ayrılmış, bunu açıklayan örnekler ve çözülmüş alıştırmalar içeren süper kapsamlı bir sayfamız var. Daha fazla ilgileniyorsanız, bu kılavuzu arama motorumuzda arayabilirsiniz (sağ üstte).