Burada kimlik fonksiyonunun ne olduğunu bulacaksınız. Ayrıca kimlik fonksiyonunun grafiksel olarak nasıl temsil edileceğini ve özelliklerinin neler olduğunu görebileceksiniz.
Kimlik işlevi nedir?
Kimlik işlevi, görüntü olarak argümanla aynı değere sahip olan işlevdir. Kimlik işlevi id terimiyle ifade edilebilir.
Bu nedenle kimlik fonksiyonunun matematiksel ifadesi şu şekildedir:
![]()
Örneğin x=1 için özdeşlik fonksiyonunun görüntüsü 1 değerinde, x=2’nin görüntüsü 2 değerinde, x=3’ün görüntüsü 3 değerinde,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
Kimlik fonksiyonu doğrusal fonksiyona bir örnektir. Aşağıdaki bağlantıda bu tür işlevlerin daha fazla örneğini görebilirsiniz:
➤ Bakınız: doğrusal fonksiyon örnekleri
Kimlik fonksiyonunun grafiksel gösterimi
Kimlik fonksiyonunun grafiği, birinci ve üçüncü çeyreğin ortaortayı olan bir çizgiye karşılık gelir.
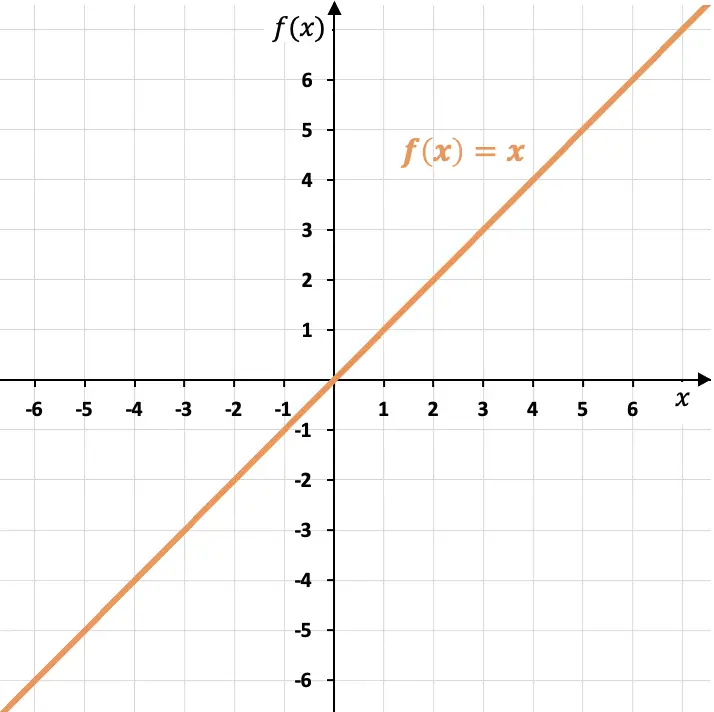
Gördüğünüz gibi kimlik fonksiyonu koordinatların orijininden ((0,0)) geçer ve değişkenin bir birimi arttığından ve bağımsızın her değeri için birliğe (m=1) eşit bir eğime sahiptir. X değişkeni. Ek olarak kimlik işlevi X ekseniyle 45°’lik bir açı oluşturur.
Kimlik fonksiyonunun özellikleri
Kimlik işlevi aşağıdaki özelliklere sahiptir:
- Kimlik fonksiyonunun etki alanı tamamen gerçek sayılardır:
![]()
- Kimlik fonksiyonunun aralığı (veya aralığı) aynı zamanda tüm gerçek sayılardan oluşur:
![]()
- Kimlik fonksiyonu sürekli ve önyargılı bir fonksiyondur.
- Ek olarak, kimlik fonksiyonu tek bir fonksiyondan oluşur; bu, koordinatların orijinine göre simetrik bir fonksiyon olduğu anlamına gelir.
![]()
➤ Bakınız: tek simetrik fonksiyon
- Kimlik fonksiyonu tüm tanım kümesinde artmaktadır ve eğimi 1’e eşittir.
![]()
- X eksenini (OX ekseni) ve y eksenini (Y ekseni) aynı noktada keser: koordinat başlangıç noktası.
![]()
- Birinci dereceden polinom fonksiyonu olarak sınıflandırılabilir.
- Kimlik işlevi, işlev bileşiminin nötr bir öğesi olarak işlev görür. Böylece, özdeşlik işleviyle oluşturulan herhangi bir işlev, işlevin kendisiyle sonuçlanır.
![]()
- Değer
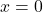
bu tür bir fonksiyonun tek köküdür.
- x artı sonsuza veya eksi sonsuza doğru yöneldiğinde özdeşlik fonksiyonunun limiti sırasıyla artı sonsuz ve eksi sonsuzu verir:
![]()
![]()
- Bu nedenle kimlik fonksiyonunun asimptotu yoktur.
- Kimlik fonksiyonunun türevi, değeri 1 olan sabit fonksiyondur:
![]()
- Kimlik fonksiyonunun integrali ikinci dereceden fonksiyondur:
![]()
➤ Bakınız: ikinci dereceden fonksiyon formülü