Kesirler veya karışık sayılar, bir miktarın diğerine bölünmesini gösteren sayısal ifadelerdir. Bu nedenle iki sayının bölümüyle temsil edilen bir değerdir. Bu tür sayılarla ondalık ve tam sayı nicelikleri ifade edebilir, hatta orantıları bile gösterebiliriz. Daha sonra kesirleri daha matematiksel bir şekilde tanımlayacağız ve size bazı örnekler göstereceğiz, böylece bu kavramı grafiksel olarak anlayabilirsiniz.
Kesirler nedir?
Kesir, eşit parçalara bölünmüş bir birimden aldığımız parça sayısına eşittir. Yani grafiksel olarak ortada yatay bir çizgiyle ayrılmış iki terimle temsil edilir. Daha doğrusu, satırın üstünde pay ve paydanın altında bulunuruz.
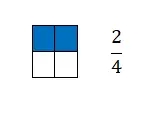
Gördüğünüz gibi kesirler oranlarla el ele gittiği için grafiğini çizmek çok kolay bir matematik kavramıdır . Bu nedenle bir önceki örnekte renkli karelerin sayısını kesirli sayı ile ifade ettik.
Kesirli terimler
Kesirin iki kısmı şunlardır:
- Pay: Bu terim yatay çizginin üstünde yer alır ve aldığımız parça sayısını buraya yazıyoruz. Pozitif, negatif ve sıfır (sıfıra eşit) payları bulabiliriz.
- Payda: Bu diğer terim çizginin altındadır ve birimin bölündüğü toplam parça sayısını buraya yazıyoruz. Pozitif ve negatif paydalar bulabiliriz ancak bunlar sıfır olamaz.
kesir türleri
Onları oluşturan sayılara ve diğer kesirlerle sundukları eşdeğerliğe bağlı olarak pek çok kesir türü vardır. Daha sonra mevcut tüm kategorileri tanımlayacağız ve onları diğerlerinden ayırmayı sağlayan özellikler hakkında yorum yapacağız:
- Uygun kesirler: Payın paydadan küçük olmasıyla oluşturulan kesirlerdir. Bu kesirleri ondalık sayıya çevirirseniz sıfır ile bir arasında bir sayı elde edersiniz. Birden büyük olamaz çünkü payın değeri her zaman paydanın değerinden küçük olacaktır ve dolayısıyla birlik aşılmayacaktır.
- Uygun olmayan kesirler: payı paydadan büyük olan kesirler, bu durumda birden büyük sayısal değerleri ifade ederler. Örneğin 8/5, 1’den büyük olan 1,6’ya eşittir. Bunlar, aşağıdaki türde olan karışık sayıları ifade etmenin başka bir yoludur.
- Karışık kesirler: Tam sayı ve karışık sayıdan oluşan kesirlere karışık sayılar da denir. Temel olarak kesirden önceki tamsayı değeriyle temsil edilirler, bu nedenle bunları bileşik kesirlere dönüştürmek için tamsayı kısmını paydayla çarpmanız, bunu paya eklemeniz ve paydayı aynı bırakmanız gerekir.
- Ondalık kesirler: Paydası on katı olan bir miktarı ifade eden kesirlerdir; örneğin: 6/10, 34/1000 veya 5/100. Bunlar ondalık gösterimde kullanılır ve en yaygın olarak tam ondalık sayıları karışık sayılara dönüştürürken kullanılır. Bunu bir sonraki bölümde daha ayrıntılı olarak ele alacağız.
- Bileşik kesirler: Payda, paydada veya her ikisinde de başka bir kesirden oluşan kesirlerdir. Bu ifadeleri basitleştirmek ve tek kesir olarak göstermek için payı paydaya bölmemiz gerekiyor. Kesirler arasındaki bölmeyi açıkladığımızda bu daha da netleşecektir.
- Eşdeğer kesirler: Aynı pay veya paydadan oluşmamasına rağmen aynı sayıya eşit olan kesirlerdir. Örneğin 8/4 = 4/2 = 2, her iki kesir de ikiye eşittir. Bu özel durumda, birinci kesir ikincinin iki katına eşit olduğundan orantılı bir ilişki korunur.
- İndirgenemez kesirler: Pay ve paydanın ortak çarpanları olmaması ve bu nedenle herhangi bir sayıya bölünememesi nedeniyle daha fazla basitleştirilemeyen kesirlerdir. Bu türün bazı örnekleri şunlardır: 9/5, 5/6, 7/8 ve diğerleri. Bunları nasıl tespit edeceğinizi bilmek için en büyük ortak bölenin nasıl hesaplanacağını bilmek önemlidir.
Kesirlerle işlemler
Artık kesirlerin farklı kategorilerini bildiğimize göre, karışık sayılarla farklı aritmetik işlemleri nasıl çözeceğimizi göreceğiz. Metodolojiyi anladığınızda her şeyin oldukça kolay olmasına rağmen, bunun tamsayılarla yapılan işlemlerden biraz daha karmaşık olduğunu belirtmek gerekir. Üstelik sadece teoriyi açıklamayacağız, aynı zamanda size bazı örnekler de göstereceğiz. Bununla birlikte, başlayalım.
kesirlerin toplamı
Ortak paydaya sahip kesirleri toplamak oldukça basittir çünkü yalnızca iki payı toplayıp paydayı aynı bırakırsınız. Öte yandan, farklı paydalara sahip kesirleri toplamak biraz zorlayıcı olabiliyor çünkü paydaların en küçük ortak katını bulmanız gerekiyor. Daha sonra, lcm’yi (yeni payda) eski paydaya bölerek her payın çarpımını eklemeliyiz. Daha iyi anlamak için aşağıdaki şemaya bakabilirsiniz:
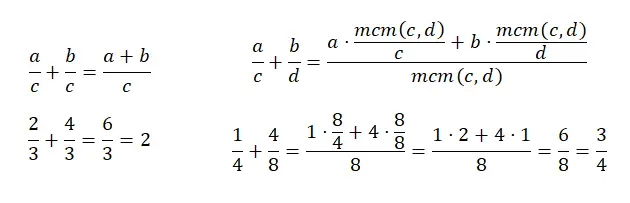
çıkarma kesirleri
Ortak paydalı kesirlerin çıkarılması toplama işlemine çok benzer, aslında payların toplamı dışında her şey aynı şekilde yapılır çünkü eklemek yerine çıkarma yapmanız gerekir. Ve farklı paydalara sahip kesirlerin çıkarılmasında da aynı şey olur, pratikte aynı şeydir, tek fark, payların çarpımını lcm’yi eski paydaya bölerek toplamak yerine çıkarmamız gerektiğidir. İşte başka bir diyagram:
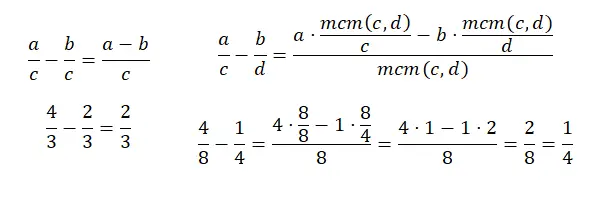
kesirlerin çarpımı
Çarpan kesirlerde paydalar aynı olsa da olmasa da aynı şekilde çözülebilir. Temel olarak payları bir parçayla, paydaları ise diğeriyle çarpmanız gerekir. Bu belki de en basit işlemdir çünkü yalnızca iki çarpma işlemi yapmanız gerekir.
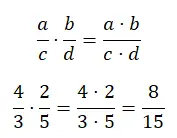
kesirlerin bölünmesi
Kesirlere bölme işlemini de çözmek oldukça kolaydır, sadece çarpı işaretlerini çarpmanız yeterlidir. Başka bir deyişle pay, birinci kesrin payını ikinci kesrin paydasıyla çarpmanın sonucudur. payda ise birinci kesrin paydası ile ikinci kesrin payının çarpımıdır.
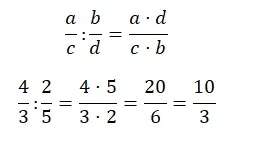
Kesirleri basitleştirin
Kesirleri sadeleştirmek veya kesirleri azaltmak bu anlamda bir aritmetik işlem değildir ancak nasıl yapılacağını bilmek çok önemlidir ve ayrıca kesir türleri ile zaten biraz üzerinde durduğumuz bir konudur. Bu nedenle, karışık bir sayıyı basitleştirmek için pay ve paydayı aynı sayıya bölmemiz gerekir. Genellikle bu sadeleştirmeyi yapmak için en büyük ortak faktörü seçeceğiz. Aşağıdaki görselde bir örnek bulabilirsiniz.
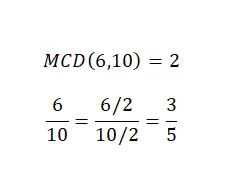
Gördüğünüz gibi iki eşdeğer kesirimiz var, yani her ikisi de aynı sayısal değeri temsil ediyor, ancak ikincisi birincisinden daha basit. Bu nedenle sadeleştirme hedefine başarıyla ulaştık.
Ondalık sayıdan kesire ve tam tersine nasıl geçilir?
Üreten kesir , ya tam bir ondalık sayı ya da tekrarlanan bir ondalık sayı olan bir ondalık sayıdan elde edilen indirgenemez kesirdir . Elbette, aşağıda tartışacağımız ondalık sayının türüne bağlı olarak farklı yöntemler kullanmamız gerekecek.
Tam ondalıktan kesir oluşturmaya dönüştürme
Bu durumda başta anlattığımız ondalık kesirlere başvurabiliriz. Basitçe, paydaki sayısal değeri ondalık nokta olmadan yazmamız gerekir. Paydaya paydaki rakam sayısı kadar sıfır içeren 10’un kuvvetini yazıyoruz.
Ancak 4,25 gibi birden büyük bir ondalık sayıya sahipsek, o zaman sahip olduğumuz tam birimlerin sayısını payda değeriyle çarpmamız ve bunu orijinal paya eklememiz gerekecektir. Aşağıda her türden bir örnek bulacaksınız:
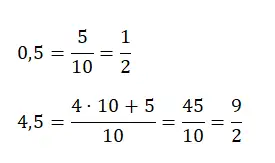
Saf yinelenen ondalık sayıyı kesir oluşturmaya dönüştürün
Saf bir periyodik ondalık sayıya sahip olduğumuzda, eğer üreten kesri elde etmek istiyorsak, paya aynı değeri koymamız, ancak ondalık nokta olmadan ve tamsayı kısmını çıkarmamız gerekir. Payda sadece dokuzlardan oluşan bir sayıya eşit olacakken, asıl sayının ondalık kısmındaki rakam sayısı kadar dokuzu özellikle yazmamız gerekiyor. Bu sistem biraz kafa karıştırıcıdır ancak birkaç örnekle şunu anlayacağız:
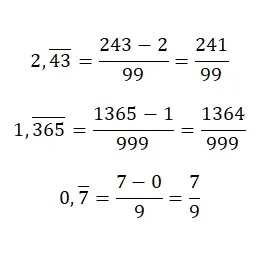
Karışık tekrarlanan ondalık sayıları kesirler oluşturmaya dönüştürün
Tekrarlanan bir ondalık sayının olması durumunda oldukça karmaşık bir kural uygulamamız gerekecek. Öncelikle payda virgül olmadan sayıyı yazacağız ve tamsayı kısmını ve ardından yinelenmeyen ondalık sayıları yine virgül olmadan çıkaracağız. Paydaya gelince, periyodik ondalık kısımdaki rakam sayısı kadar dokuz, ardından yinelenmeyen ondalık kısımdaki rakam sayısı kadar sıfır yazmanız gerekecektir.
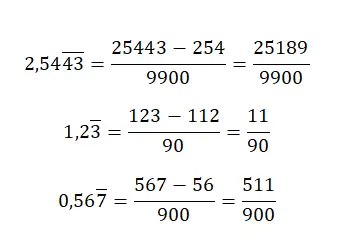
kesri ondalık sayıya dönüştür
Kesirden ondalık sayıya geçmek için payı paydaya bölmeniz yeterlidir; çünkü karışık sayı , iki değer arasındaki bölümden başka bir şey değildir. Yani bölümü çözerek karşılık gelen ondalık sayıyı elde edersiniz. Aşağıdaki görselde oldukça basit bazı örnekler bulabilirsiniz:
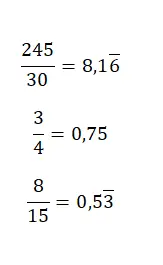
kesirler egzersizleri
Artık kesirlerle ilgili tüm teoriyi bildiğinize göre, bazı alıştırmalar yapmanızı öneririz. Bu sayede anlatılan tüm kavramları daha derinlemesine öğrenecek ve sınav günü hesaplamaları çözmede daha hızlı ilerlemiş olacaksınız. Ek olarak, mevcut tümkesir alıştırmalarını görmüş olacaksınız ve bunları buna göre nasıl çözeceğinizi bileceksiniz. Son olarak, tüm kesir işlemlerini çözebileceğiniz çevrimiçi bir kesir hesaplayıcımızın da emrinizde olduğunu söyleyeyim.