Düzlemdeki iki çizginin göreceli konumu

Bu sayfada, düzlemdeki (R2’deki) iki çizginin göreceli konumunu belirlemek için mevcut olan farklı yöntemlerin açıklamasını bulacaksınız. Ayrıca çeşitli örnekler göreceksiniz ve adım adım çözülen alıştırmalar ile pratik yapabileceksiniz.

Düzlemdeki iki doğrunun göreceli konumu nedir?

Düzlemdeki iki çizgi arasındaki göreceli konumlara bakmadan önce, elbette bir çizginin tam olarak ne olduğunu bilmeniz gerekir, bunu çizgi tanımında bulabilirsiniz.

Bu nedenle, iki boyutta (R2’de) çalışırken, iki çizgi arasında 3 tür olası göreceli konum vardır:

Kesişen çizgiler

Kesişen iki doğrunun yalnızca bir ortak noktası vardır.

Paralel çizgiler

Ortak noktaları yoksa iki doğru paraleldir. Yani eğer yolları hiç kesişmezse.

çakışan çizgiler

İki doğrunun bütün noktaları ortaksa aynıdır.

Öte yandan düzlemdeki iki çizgi arasındaki açı da onların göreceli konumlarına bağlıdır:

Kesişen çizgiler 0° (dahil değil) ile 90° (dahil) arasında bir açıyla kesişir. Ek olarak, eğer sadece 90 derecelik bir dik açı oluşturuyorlarsa bu, iki çizginin birbirine dik olduğu anlamına gelir.
Paralel doğrular aynı yöne sahip olduklarından 0° açı oluştururlar.
Ve aynı nedenle çakışan çizgiler de aralarında 0°’lik bir açı yapar.

İki çizgi arasındaki açının nasıl hesaplandığını öğrenmek istiyorsanız iki çizgi arası açı formülüne göz atabilirsiniz. Burada iki çizgi arasındaki açının nasıl belirleneceğine ilişkin ayrıntılı bir açıklamanın yanı sıra birkaç örnek ve hatta çözülmüş alıştırmalar bulacaksınız; böylece konsepti pratik edebilir ve tam olarak anlayabilirsiniz.

Düzlemde iki çizginin göreceli konumu nasıl bulunur?

İki boyutlu uzayda iki çizgi arasındaki göreceli konumu bilmek, çizgilerin nasıl ifade edildiğine bağlıdır:

Çizgi yön vektörleri: İki doğrunun yön vektörü farklıysa kesişmeleri gerekir. Öte yandan yön vektörlerinin koordinatları eşit veya orantılı ise paralel veya çakışabilir (ortak noktaları olup olmadığını kontrol etmek gerekir).

Açık denklem: iki doğrunun eğimleri farklı olduğunda
$(m)$

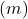
Tam tersine, çizgiler aynı eğime sahip ancak orijinde farklı bir sıraya sahipse

$(n)$

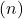
paraleldirler. Son olarak, başlangıçta eşit eğimlere ve koordinatlara sahip olan iki çizgi karıştırılır.

Genel (veya örtülü) denklem: A ve B orantısız katsayılara sahip iki doğru her zaman kesişecektir. Ancak bu iki parametre birbiriyle orantılı olup C katsayısıyla orantılı olmadığında paralel olacaktır. Ve son olarak üç terim orantılı olduğunda bu durum çizgilerin karıştığı anlamına gelir.

Yukarıdaki doğrunun denklemleri hakkında şüpheniz varsa düzlemdeki doğrunun denklemlerinin açıklamasına başvurabilirsiniz. Burada tüm çizgi denklemlerinin formüllerini, nasıl hesaplandıklarını, örneklerini ve çizgi denklemlerinin çözülmüş alıştırmalarını bulacaksınız.

Aşağıdaki tabloda önceki özelliklerin bir özeti bulunmaktadır:

Daha sonra, iki çizgi arasındaki göreceli konumun nasıl belirleneceğine ilişkin iki örnek göreceğiz:

örnek 1

Açık bir denklem biçiminde tanımlanan aşağıdaki iki çizgi arasındaki göreceli konumu bulun:

$r: \ y=3x+2 \qquad \qquad s: \ y=3x-4$

İki çizgi aynı eğime sahiptir:

$m_r = m_s = 3$

Ancak başlangıçta farklı bilgisayarları var:

$n_r =2\neq n_s=-4$

Yani eğimleri aynı fakat kesişme noktaları farklı olduğundan çizgiler paraleldir .

Örnek 2

Örtülü (veya genel) denklemleriyle ifade edilen aşağıdaki iki çizgi arasındaki göreceli konumu belirleyin:

$r: \ 4x+2y-6=0 \qquad \qquad s: \ -2x-y+3=0$

Her iki çizgi de açık bir denklem olarak ifade edilir, dolayısıyla katsayılarından herhangi birinin orantılı olup olmadığını görmemiz gerekir:

$\cfrac{4}{-2}=\cfrac{2}{-1} = \cfrac{-6}{3} = -2$

Doğruların 3 terimi orantılı olduğundan çizgiler çakışır .

Düzlemdeki iki çizginin göreceli konumunu bir denklem sistemiyle belirleyin

İki çizgi arasındaki göreceli konumu bilmenin bir başka yolu da çizgilerin denklemlerinden oluşan denklem sistemini analiz etmektir:

Sistemin tek bir çözümü varsa çizgiler kesişir. Ayrıca iki doğrunun kesişme noktası sistemin çözümüdür.
Çözümü olmayan bir sistem ise bu, doğruların ortak noktalarının bulunmadığını ve dolayısıyla paralel doğrular olduklarını gösterir.
Sistemin sonsuz sayıda çözümü varsa , bu, doğruların tüm noktalarının ortak olduğu ve dolayısıyla kesişen doğrular olduğu anlamına gelir.

Örnek 3

Aşağıdaki iki doğrunun göreceli konumunu bir denklem sistemi kullanarak hesaplayın:

$r: \ 3x+4y+5=0 \qquad \qquad s: \ 5x+y-3=0$

İki doğrunun göreceli konumunu bulmak için iki doğrunun oluşturduğu aşağıdaki doğrusal denklem sistemini çözmemiz gerekir:

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}$

Bu durumda sistemi ikame yöntemiyle çözeceğiz. Bu nedenle değişkeni izole edeceğiz

$y$

ikinci denklemden alıp birinci denklemde yerine koyalım:

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}$

$3x+4(3-5x)+5=0$

$3x+12-20x+5=0$

$3x-20x=-12-5$

$-17x=-17$

$x=\cfrac{-17}{-17} = 1$

Ve bilinmeyenin ne kadar değerli olduğunu bildiğimizde

$x$

Değerini aşağıdaki ifadenin yerine koyarız:

$y:$

$y=3-5x \ \xrightarrow{x \ = \ 1} \ y = 3 -5\cdot 1$

$y = 3 -5 = -2$

Bu nedenle iki doğrudan oluşan denklem sisteminin yalnızca bir çözümünü elde ettik, yani iki doğru kesişiyor . Ve bunların kesiştiği nokta sistemin çözümü yani noktadır.

$(1,-2).$

Düzlemdeki iki çizginin göreceli konumuyla ilgili çözülmüş problemler

1. Egzersiz

Aşağıdaki doğruların kesişip kesişmediğini, paralel mi yoksa çakışık mı olduğunu belirleyin:

$r: \ 3x-y+4=0 \qquad \qquad s: \ 9x-3y+3=0$

Çözüme bakın

Her iki çizgi de örtülü (veya genel) bir denklem olarak ifade edilir, bu nedenle katsayılarından herhangi birinin orantılı olup olmadığını görmemiz gerekir:

$\cfrac{3}{9}=\cfrac{-1}{-3} \neq \cfrac{4}{3}$

Doğruların yalnızca A ve B katsayıları birbirleriyle orantılıdır, C katsayısıyla orantılı değildir. Bu nedenle iki doğru paraleldir .

Alıştırma 2

Parametrik denklemlerle ifade edilen aşağıdaki iki çizgi arasındaki göreceli konumu bulun:

$\displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}$

Çözüme bakın

Göreli konumlarını bulmak için iki doğrunun oluşturduğu denklem sistemini çözebiliriz. Ancak parametrik denklemler şeklinde oldukları için yön vektörleri kolaylıkla bulunabilir ve eğer orantılı değillerse doğruların kesiştiği anlamına gelir. Ve bu durumda, bütün bir denklem sistemini çözmek için çok fazla zaman harcamayacağız.

Böylece her satırın yön vektörünün Kartezyen koordinatları parametrenin önündeki sayılardır.

$t:$

$\vv{r} =(-5,3) \qquad \qquad \vv{s}=(-2,9)$

Yön vektörlerini öğrendikten sonra orantılarını kontrol ederiz:

$\cfrac{-5}{-2} \neq \cfrac{3}{9}$

Yön vektörleri orantılı değildir, dolayısıyla çizgiler birbirini keser .

Alıştırma 3

Aşağıdaki doğruların kesişip kesişmediğini, paralel mi yoksa çakışık mı olduğunu belirtin ve ayrıca aralarında bir kesişme noktası bulun (varsa).

$r: \ y=4x-5 \qquad \qquad s: \ y=-2x+7$

Çözüme bakın

İki çizgi açık denklemleriyle tanımlanır ve farklı eğimlere sahiptir:

$m_r =4 \neq m_s = -2$

Eğimleri farklı olduğundan doğrular kesişir .

Dolayısıyla doğrular kesiştiği için ortak 1 noktası olacaktır ve bunu hesaplamak için iki doğrunun oluşturduğu denklem sistemini çözmemiz gerekir:

$\left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}$

Bu durumda sistemi eşitleme yöntemiyle çözeceğiz çünkü her ikisi de

$y$

zaten silindi:

$y=y$

$4x-5=-2x+7$

$4x+2x=5+7$

$6x=12$

$x=\cfrac{12}{6} = 2$

Ve bilinmeyene sahip olduğumuzda

$x$

değerini herhangi bir ifadede değiştiririz

$y$

ne kadar değerli olduğunu öğrenmek için:

$y=4x-5$

$y = 4\cdot 2 -5 = 8 -5 = 3$

Yani iki doğrunun kesişme noktası sistemin sonucudur:

$\bm{(2,3)}$

Alıştırma 4

Bilinmeyenlerin değerini hesaplayın

$a$

$b$

aşağıdaki iki çizgi paralel olacak şekilde:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

Çözüme bakın

Çizgiler genel (veya örtülü) denklem formunda açıklanmaktadır. Dolayısıyla iki doğrunun paralel olabilmesi için A ve B katsayılarının orantılı olması yani aşağıdaki denklemin gerçekleşmesi gerekir:

$\cfrac{2}{1} = \cfrac{-4}{a}$

Bu nedenle bilinmeyenin değerini elde etmek için önceki denklemi çözmeliyiz.

$a.$

Bunu yapmak için kesirleri çapraz olarak çarpıyoruz:

$2 \cdot a = -4 \cdot 1$

$a = \cfrac{-4}{2}$

$\bm{a=-2}$

Öte yandan doğruların paralel olması için bağımsız terimleri diğer katsayılarla orantılı olamaz:

$\cfrac{2}{1} \neq \cfrac{6}{b}$

Bu nedenle, daha önce olduğu gibi, kesirleri çapraz olarak çarparak eşitsizliği çözüyoruz:

$2 \cdot b \neq 6 \cdot 1$

$b \neq \cfrac{6}{2}$

$\bm{b\neq 3}$

Kısacası iki doğru paralel olsun

$a$

2 olmalı ve

$b$

3 dışında herhangi bir reel sayı olabilir.

Alıştırma 5

Doğruya paralel doğrunun açık denklemini bulun

$r$

ve bu noktada ne olur?

$P(3,-1).$

düz olmak

$r:$

$r: \; y=2x+5$

Çözüme bakın

Böylece çizgi çizgiye paralel olur

$r,$

her ikisinin de aynı eğime sahip olması gerekir. ve çizginin eğimi

$r$

$m = 2$

Buna göre bulmamız gereken doğrunun denklemi şu şekilde olacaktır:

$y=2x+n$

Doğrunun eğimini bildiğimizde, doğruya ait olan noktayı doğru denkleminde değiştirerek y kesme noktasını hesaplayabiliriz:

$P(3,-1)$

$y= 2x+n \ \xrightarrow{x=3 \ ; \ y=-1} \ -1=2\cdot 3 +n$

$-1=6+ n$

$-1-6= n$

$-7= n$

Dolayısıyla doğrunun açık denklemi şöyledir:

$\bm{y=2x-7}$

Buraya kadar başardıysanız, plandaki iki çizgi arasındaki göreceli konumlara zaten hakim oldunuz demektir. Tebrikler!

Ancak birçok kişinin merak ettiği şey şu: İki çizgi arasındaki göreceli konumu bilmenin ne faydası var?

Çizgiler arasındaki göreceli konumun uygulamalarından biri, iki çizgi arasındaki mesafeyi bilmektir, çünkü iki çizgi arasındaki mesafenin hesaplanması, bunların göreceli konumuna bağlıdır:

Çizgiler kesişiyor veya çakışıyorsa mesafe sıfırdır.
Öte yandan çizgiler paralel olduğunda belirli bir formülün uygulanması gerekir. Eğer daha çok ilginizi çekiyorsa iki paralel çizgi arasındaki mesafenin nasıl hesaplandığına göz atabilirsiniz.

Düzlemdeki iki doğrunun göreceli konumu nedir?

Düzlemde iki çizginin göreceli konumu nasıl bulunur?

örnek 1

Örnek 2

Düzlemdeki iki çizginin göreceli konumunu bir denklem sistemiyle belirleyin

Örnek 3

Düzlemdeki iki çizginin göreceli konumuyla ilgili çözülmüş problemler

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Yorum bırakın Yanıtı iptal et