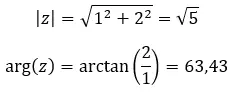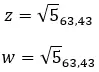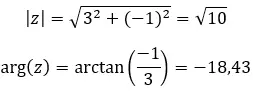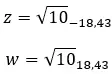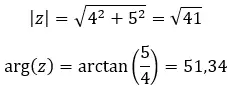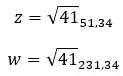Bu yazımızda hesaplamaları çözerken ve ifadeleri basitleştirirken faydalı olabilecek karmaşık sayıların özelliklerini tartışacağız. Şimdi doğrudan bu özelliklere geçelim.
Karmaşık bir sayının modülü ve argümanı
Karmaşık sayının ilk özelliği, karmaşık sayının modülü ve argümanıdır. Hesaplaması çok kolaydır çünkü sadece birkaç formülü uygulamanız yeterlidir.
Modülü hesaplamak için formül:

Argümanı hesaplamak için formül:

Artık sayı kutupsal veya trigonometrik biçimde ifade edilirse herhangi bir hesaplama yapmaya gerek yoktur. Çünkü aynı ifadede modül ve argüman listelenmiştir.
Aşağıdaki resimde bir sayının formülünü kutupsal biçimde görebilirsiniz; burada |z| modül ve α argümandır.

Ve bu diğer resimde trigonometrik formda ifade edilen bir sayının yapısını görebilirsiniz; burada |z| modül ve α argümandır.

eşit karmaşık sayılar
Eşit karmaşık sayılar, modülü ve argümanı paylaşanlardır. Yani, bu iki değerden:

Aşağıdaki özellik karşılanırsa bunlar aynıdır.
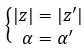
Öte yandan, eğer her iki sayı da binom formundaysa, bunların iki eşit karmaşık sayı olup olmadığını görmek için çok hızlı ve kolay bir kontrol yapabiliriz. Basitçe aşağıdaki ifadenin yerine getirilmesi gerekir:
a + bi = a + bi
Bir örnek görelim ve aşağıdaki iki karmaşık sayının eşit olup olmadığını belirleyelim:
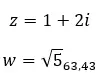
Karmaşık sayıların eşleniği
Şimdi karmaşık sayıların en önemli özelliklerinden birine geçelim, çünkü bir kompleksin eşleniğinin nasıl hesaplanacağını bilmek, karmaşık bölmeleri çözmede ve sadeleştirmeler yapmada bize çok yardımcı olur.
Yani, bu iki değerden:

Bir modülü paylaşıyorlarsa ve karşıt argümanlara sahiplerse konjuge olduklarını söyleriz. Bu nedenle tamamlanması gerekir:
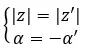
Öte yandan, eğer her iki sayı da binom formundaysa, bunların iki karmaşık eşlenik sayı olup olmadığını görmek için çok hızlı ve kolay bir kontrol yapabiliriz. Basitçe aşağıdaki ifadenin yerine getirilmesi gerekir:
un + bi = un – bi
Bir örnek görelim ve aşağıdaki iki karmaşık sayının eşlenik olup olmadığını belirleyelim:
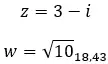
Karmaşık sayıların tersi
Daha sonra zıt karmaşık sayıların özelliğini görmeye geçiyoruz. Bu iki değerden:

Aynı modüle sahiplerse ve argümanları 180 derece veya π radyan kadar farklıysa, bunların zıt olduklarını söyleyebiliriz:
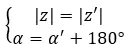
Öte yandan, eğer her iki sayı da binom formundaysa, bunların zıt iki karmaşık sayı olup olmadığını bulmak için daha hızlı ve daha basit başka bir yöntem kullanabiliriz. Basitçe aşağıdaki ifadenin yerine getirilmesi gerekir:
a + bi = -a – bi
Bir örnek görelim ve aşağıdaki iki karmaşık sayının zıt olup olmadığını belirleyelim:
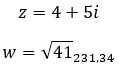
diğer özellikler
Açıkçası, bu sayı kümesinin ters karmaşık sayılar gibi başka özellikleri ve temel aritmetik işlemlerle doğrudan ilgili birkaç özelliği daha vardır. Bunların hepsi diğer makalelerde ele alınsa da bunları aşağıdaki listede görebilirsiniz.
Karmaşık sayıların özelliklerini öğrenin
- Karışık sayılar
- Karmaşık sayılarla işlemler
- karmaşık kökler
- Karmaşık sayıların grafiksel gösterimi