Muhtemelen karmaşık sayıları duymuşsunuzdur. Bunlar belki de başa çıkılması en zor sayı kümesidir çünkü gerçek ve sanal sayıları birleştirirler. Birleştirilmesi, tüm gerçek sayılar kullanılarak tedavi edilemeyen sayısal davranışların incelenmesini mümkün kılar.
Karmaşık sayılar nelerdir?
Karmaşık sayılar bir reel sayı ile bir sanal sayının birleşimidir. Örneğin 4 + 5i , gerçek kısmı 4’e ve sanal kısmı 5i’ye eşit olan karmaşık bir sayıdır. Genel olarak bunları aşağıdaki formülle ifade edebiliriz:
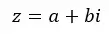
Burada Re(z) = a ve Im(z) = b
Daha önce de söylediğimiz gibi kompleksler hem gerçek sayıları hem de sanal sayıları içeren en büyük küme veya küresel kümedir . Daha sonra size tüm kümelerin hiyerarşik yapısının küçük bir diyagramını gösteriyoruz:

Bu nedenle, bir gerçel sayı ile sanal bir sayının birleşimine sahip olduğumuzda, karmaşık bir sayıya sahip oluruz. Ancak iki kısımdan birinin sıfıra eşit olduğu zamanlar vardır. Bu durumlarda ne olur? Hala komplekslerle uğraşıyoruz çünkü karmaşık küme diğer tüm sayısal kümeleri kapsar. Ancak farklı bir alt kategoriye giriyoruz:
| karmaşık sayı | kraliyet partisi | hayal gücü kısmı | Alt kategori |
| 2+5i | 2 | 5i | Karmaşık |
| 4 | 4 | 0 | saf kraliyet |
| 3i | 0 | 3i | Saf hayalgücü |
Saf bir reel değere sahip olduğumuzda, sanal değer b sıfıra eşit olduğundan, kalan karmaşık sayı şuna eşdeğerdir:
z = a + 0i = a
Öte yandan, saf bir hayal gücümüz olduğunda, a sıfıra eşit olur ve sonuç olarak karmaşık sayı şu şekilde kalır:
z = 0 + bi = bi
Karmaşık sayıların grafiksel gösterimi
Karmaşık sayıları temsil etmek için karmaşık düzlemi kullanırız. İki çizgiden oluşur: gerçek çizgi ve sanal çizgi. Bu iki sayı doğrusu, her kümedeki sayıları grafiksel olarak konumlandırmak için kullanılır ve bunları bir araya getirirsek aşağıdaki gibi bir plan elde ederiz:

X eksenine gerçek eksen denir çünkü burası gerçek kısım değerlerinin bulunduğu yerdir. Y ekseni sanal eksen olarak adlandırılırken sanal değerlerin yazıldığı yer burasıdır. Bir örnek görelim, 3 + 2i sayısını karmaşık düzleme yerleştireceğiz.

Resimde gördüğünüz gibi her biri bir eksen için olan 3 ve 2 rakamlarını koordinat olarak kullanarak sayıyı bulduk. Karmaşık sayıları temsil etme hakkında daha fazla bilgi edinmek istiyorsanız bu makaleyi okumanızı öneririz.
Karmaşık sayıların türleri nelerdir?
Şimdi karmaşık bir sayıyı nasıl ifade etmemiz gerektiğini göreceğiz. Şu ana kadar yalnızca toplam olarak yazılan temel formu (binom formu olarak adlandırılır) gördük: gerçek kısım artı sanal kısım.
Ancak gerçekte üç biçimimiz var: binom, kutupsal ve trigonometrik . Her ifade türünün kendine has özellikleri vardır ve şu veya bu durumda kullanılır. Yani hepsini açıklayacağız ve birinden diğerine nasıl geçeceğimizi göstereceğiz.
1. Binom formu
Binom formundaki karmaşık sayılar, gerçek kısım ile sanal kısmın toplamı olarak yazılır: a + bi. Örneğin 6 + i sayısı binom gösterimiyle ifade edilen bir komplekstir. Bunda formül her zaman aynıdır:

Bu nedenle karmaşık bir sayıyı binom biçiminde ifade etmek için yalnızca gerçek değerini ve sanal değerini bilmeniz gerekir.
Örneğin 3 + 2i değeri binom formundadır ve daha önce gördüğümüz gibi şu şekilde temsil edilir:

Binom formu esas olarak karmaşık sayılarda toplama ve çıkarma işlemlerini çözmek için kullanılır.
2. Kutupsal form
Karmaşık sayıları kutupsal biçimde ifade etmek için |z| modülünü hesaplamamız gerekir. ve onun argümanı. Kutupsal form esas olarak karmaşık sayılarda çarpma ve bölme işlemlerini çözmemiz gerektiğinde kullanılır.
Karmaşık sayının modülünü hesaplamak için aşağıdaki formülde açıklandığı gibi a ve b’nin modülünü yapmanız yeterlidir:

Z’nin argümanını veya açısını hesaplamak için b’nin a arasındaki arktanjantını hesaplamamız gerekir:

α açısının değerini tam olarak belirlemek için hangi çeyrekte bulunduğunun belirlenmesi gerektiğine dikkat etmek önemlidir. Aslında arktanjant fonksiyonu yalnızca π/2 ile -π/2 arasındaki açıları hesaplar. Karmaşık sayının hangi çeyrekte bulunduğunu belirtmek için a ve b değerlerine bakmalıyız (pozitif veya negatifse):
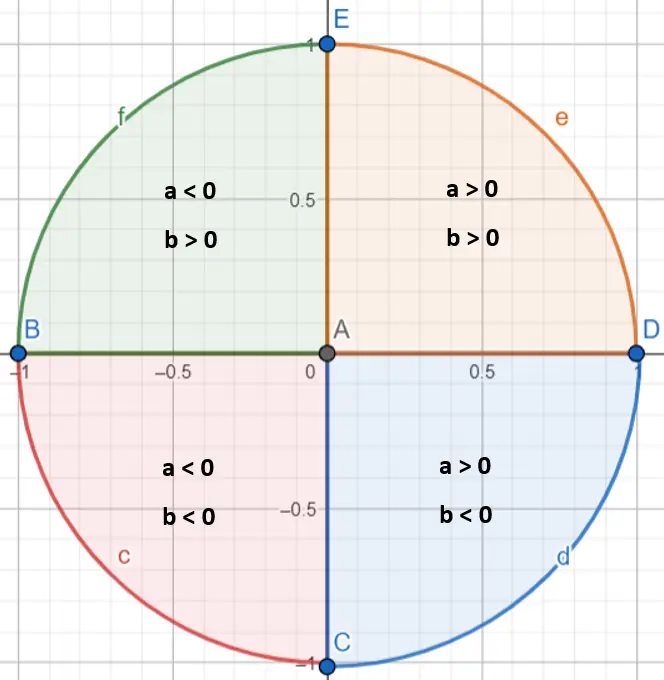
Sayımızın hangi çeyreğe düştüğünü öğrendikten sonra birkaç kurala uymamız gerekiyor:
- Eğer karmaşık sayı birinci çeyrekte ise (a > 0 ve b > 0), argümanı olduğu gibi bırakacağız.
- Karmaşık sayı ikinci çeyrekte ise (a < 0 ve b > 0), argümana π’yi ekleyeceğiz.
- Karmaşık sayı üçüncü çeyrekte ise (a < 0 ve b < 0), π’yi argümandan çıkarırız.
- Karmaşık sayı dördüncü çeyrekte ise (a > 0 ve b < 0), argümana 2π ekleyeceğiz.
Çeyrek daire derken neyden bahsettiğimizi bilmiyorsanıztrigonometrik oranlar yazımıza göz atmanızı tavsiye ederiz.
Z’nin büyüklüğünü ve argümanını bildiğimizde karmaşık sayıyı kutupsal biçimde ifade edebiliriz. Bu form birkaç terminolojiyi kabul etse de, iki ana isim şunlardır:

Örneğin 3 + 5i sayısını polar olarak değiştirmek istiyorsak aşağıdaki prosedürü izlememiz yeterlidir.
İlk önce modülü hesaplıyoruz:
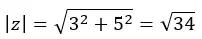
Daha sonra ilk çeyrekteki argümanı hesaplıyoruz, böylece hesapladığımız gibi kalıyor.
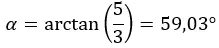
Ve sayıyı kutupsal biçimde ifade ederiz:
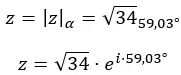
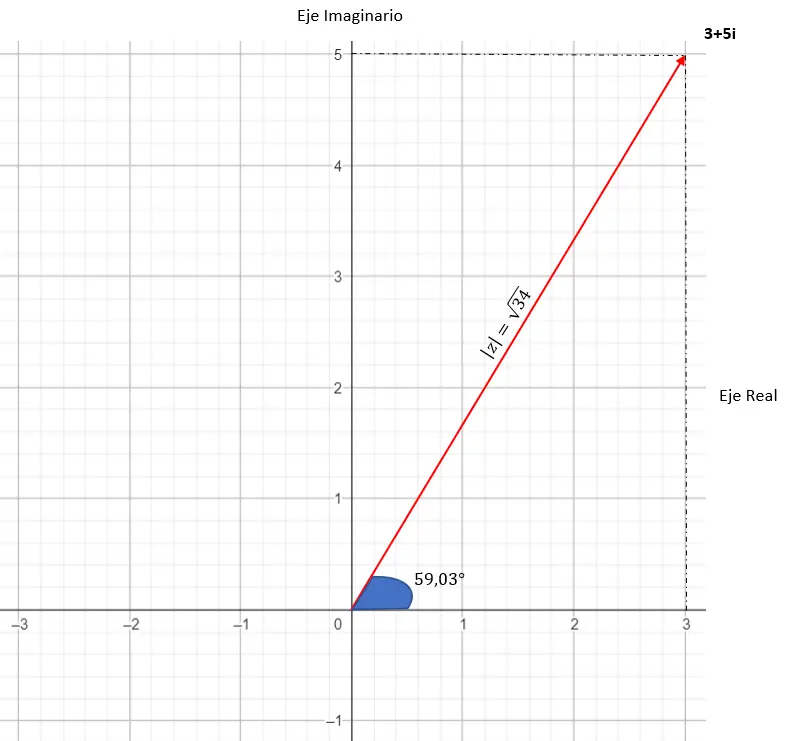
Grafik gösterimi aşağıdaki gibidir:
3. Trigonometrik form
Son olarak Euler formülünden hesaplanan trigonometrik gösterime sahibiz:

Örneğin 4 – 3i sayısını trigonometrik biçimde ifade etmek için aşağıdaki prosedürü takip ederiz:
Polar form bölümünde kullandığımız formüllerle modülü ve argümanı hesaplayarak başlıyoruz.
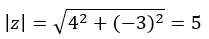
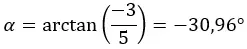
DİKKAT: Argüman dördüncü çeyrektedir çünkü (a > 0 ve b < 0).
Verileri trigonometrik formda denklemin içine ekliyoruz.
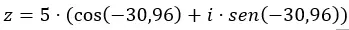
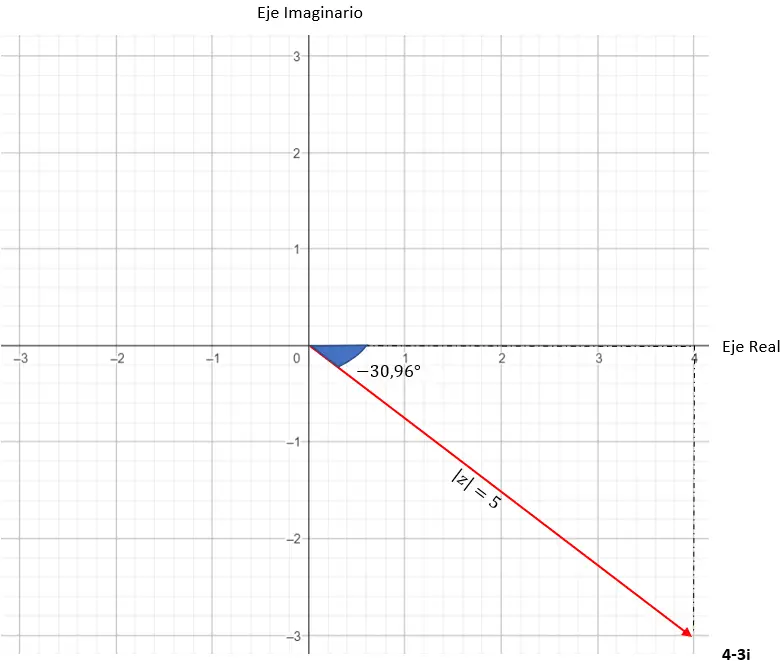
Ve zaten trigonometrik formda ifade edilen sayıya sahibiz. Grafik gösterimi aşağıdaki gibidir.
Bir türden diğerine nasıl geçilir?
Artık karmaşık bir sayıyı ifade etmenin tüm yollarını biliyorsunuz. Son bölüm boyunca her birine nasıl erişeceğinizi görebildiniz, ancak bitirmeden önce bir formdan diğerine nasıl geçeceğimize dair kısa bir özet vermek istiyoruz. Yalnızca önceki bölümde gördüğümüz formülleri kullanmanız gerekir.
Binomdan kutupsal forma ve tersi
Binomdan kutupsala geçmek için aşağıdaki diyagramı öneriyoruz:
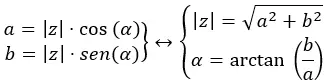
Daha önce iki terimliden kutupsala gittiğimiz bir örneği görmüştük, şimdi yukarıdaki diyagramı kullanarak kutupsaldan binomiyele gideceğiz. √41 38,66’yı binoma dönüştürmemiz gerekiyor.
İlk önce a’yı hesaplıyoruz.
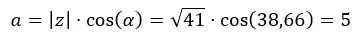
Daha sonra b’yi hesaplıyoruz.
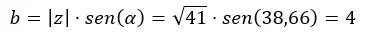
Ve bunu binom formunda ifade ediyoruz.
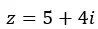
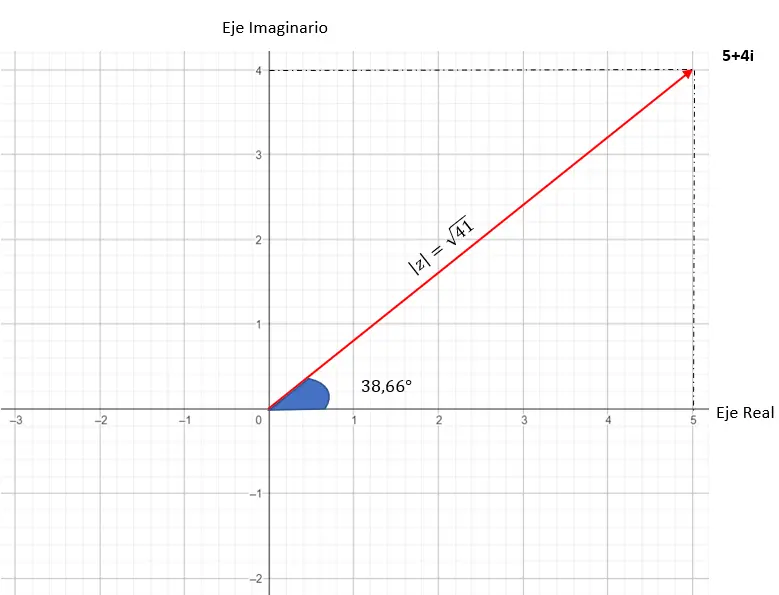
Bu sayının grafiksel gösterimi şuna benzer:
Binom formundan trigonometrik forma ve tam tersi
Binomdan trigonometriye geçmek için önceki bölümde bahsettiğimiz formülleri de uygulamanız gerekiyor. Bu şekilde önce modülü ve argümanı hesaplıyoruz, ardından bu verileri trigonometrik formun denklemine yerleştiriyoruz. Örnek vermek gerekirse trigonometrik olarak z = 3 + 2i sayısını aktaracağız.
İlk önce modülü ve argümanı hesaplıyoruz.
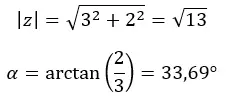
DİKKAT: Argüman birinci çeyrektedir çünkü (a > 0 ve b > 0).
Daha sonra trigonometrik form denklemini bu verilerle tamamlıyoruz.
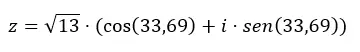
Trigonometriden binoma geçmek istiyorsak tek yapmamız gereken önceki ifadeyi çözmek.
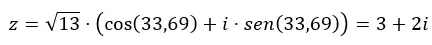
Polar formdan trigonometrik forma ve tersi
Son olarak kutupsal formdan trigonometrik forma geçeceğiz. Bu oldukça basit çünkü bu iki biçim aynı iki değerle ifade ediliyor: modulo ve argüman . Yani sadece formları doldurmanız yeterli, hepsi bu.
Örnek verelim z = √85 12.53 sayısını trigonometrik forma çevireceğiz.
Trigonometrik formun denkleminde iki değişkeni (modül ve argüman) yeniden formüle ediyoruz:
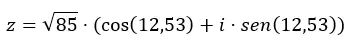
Artık bir formdan diğerine nasıl geçeceğinizi bildiğinize göre, birkaç alıştırma ile biraz pratik yapmanızı öneririz. Bu şekilde bu makalede öğrenilen bilgileri pekiştireceksiniz. Bu konuyla ilgili herhangi bir sorunuz varsa, bunları yorumlarda bırakmaktan çekinmeyin. Karmaşık sayılar hakkında daha fazla bilgi edinmek istiyorsanız aşağıdaki bağlantılara göz atın.
Karmaşık sayılar hakkında daha fazla bilgi
- hayali sayılar
- Karmaşık sayıların özellikleri
- Karmaşık sayılarla işlemler
- karmaşık sayıların kökleri
- Karmaşık sayıların grafiksel gösterimi