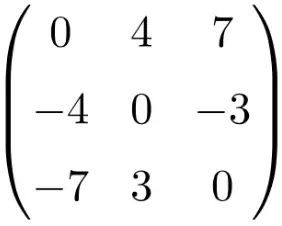Bu sayfada kare matrisin ne olduğunu açıklayacağız ve kare matris örneklerini bulacaksınız. Ayrıca kare matrislerin hangi özelliklere sahip olduğunu, onlarla yapılabilecek işlemleri ve mevcut farklı türlerini göreceksiniz.
Kare matris nedir?
Bir kare matris bir Satır sayısı sütun sayısıyla aynı olan matris.
Kare matris örnekleri
2. dereceden kare matris
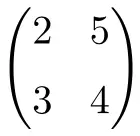
3. dereceden kare matris
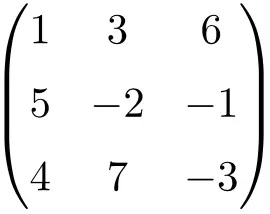
4. dereceden kare matris
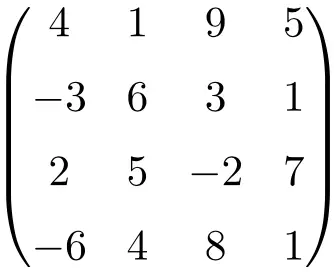
Gördüğünüz gibi, kare matrisler genellikle sıralarına göre adlandırılır, yani 2. mertebeden bir kare matris, bunun 2×2 boyutunda bir matris olduğu anlamına gelir (2 satır ve 2 sütun), veya 3. mertebeden bir kare matristen bahsediyoruz. bu da 3×3 (3 satır ve 3 sütun) boyutunda olduğunu gösterir.
Bir kare matrisin köşegenleri
Kare matrislerin köşegenlerinin belirli isimleri vardır; ana köşegen ve ikincil köşegen vardır:
- Bir kare matrisin ana köşegeni, sol üst köşeden sağ alt köşeye giden öğelerden oluşur:

- Bir kare matrisin ikincil köşegeni, sol alt köşeden sağ üst köşeye giden öğelere karşılık gelir:

Kare matrisin özellikleri
Kare matrisler doğrusal cebirde yaygın olarak kullanılır, bu yüzden çok önemlidirler. Şimdi bu matris sınıfını bu kadar anlamlı kılan özelliklerin neler olduğuna bakalım:
- Herhangi bir kare matris, bir simetrik matris ve bir antisimetrik matrisin toplamına ayrıştırılabilir.
- İki kare matris aynı mertebedeyse bunlar birbirine eklenebilir veya çıkarılabilir :
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- İki kare matris her iki olası yönde de çarpılabilir . Ancak kare matrislerin çarpımı değişmeli değildir, yani hangi tarafla çarpıldığına bağlı olarak çarpma sonucu değişecektir. Aşağıdaki örnekte sonucun matrislerin konumlarına nasıl bağlı olduğuna dikkat edin:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- Determinantı hesaplayabilenler yalnızca kare matrislerdir. Bu nedenle bir determinant ancak kare matris ise çözülebilir . Örneğin, 3×3 kare matrisin determinantını bulmak için Sarrus kuralını uygulamanız gerekir:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
Ayrıca matrisin determinantının 0’dan farklı olması onun normal bir matris olduğu, yani tersinir olduğu anlamına geldiğini unutmayın. Öte yandan, eğer determinant sıfır ise, bu tekil bir matristir (tersi yoktur).
- Son olarak kare matrisler köşegenleştirilebilir . Böylece bir kare matrisin özdeğerlerini (veya özdeğerlerini) ve özvektörlerini (veya özvektörlerini) hesaplamak için taban değişikliği gerçekleştirilebilir.
Kare matrislerle işlemler
Gördüğümüz gibi bir matrisin determinantı ancak matrisin kare olması durumunda hesaplanabilir. Aynı şekilde matrisin yalnızca kare boyutlu olması durumunda gerçekleştirilebilecek belirli işlemler de vardır:
bir matrisin izi
Bir matrisin izi, bir kare matrisin ana köşegenini oluşturan elemanların toplamıdır.
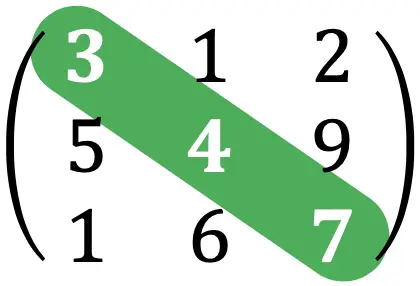
Örneğin, yukarıdaki alıştırmadan elde edilen matrisin izi şu şekilde olacaktır:
![]()
Kare kalıp çeşitleri
O zaman var olan en önemli kare matris türlerine sahipsiniz. Özelliğini öğrenmek için kalıp tipine tıklayın.
Gördüğünüz gibi birçok kare matris türü vardır ve her birinin farklı bir nedenden dolayı kendi adı vardır.