Jacobian ve Jacobian matrisi

Bu sayfada Jacobian matrisinin ne olduğunu ve bir örnek kullanarak nasıl hesaplanacağını bulacaksınız. Ayrıca pratik yapabilmeniz için Jacobian matrisleri üzerine çözülmüş birkaç alıştırmanız var. Ayrıca Jacobian matrisinin determinantı Jacobian’ın neden bu kadar önemli olduğunu da göreceksiniz. Son olarak bu matrisin diğer işlemlerle olan ilişkilerini ve sahip olduğu uygulamaları açıklıyoruz.

Jacobian matrisi nedir?

Jacobian matrisinin tanımı aşağıdaki gibidir:

Jacobian matrisi, bir fonksiyonun birinci dereceden kısmi türevlerinden oluşan bir matristir.

Jacobian matrisinin formülü bu nedenle aşağıdaki gibidir:

Bu nedenle Jacobian matrisleri her zaman skaler fonksiyonlar kadar satıra sahip olacaktır.

$(f_1,f_2,\ldots ,f_m)$

fonksiyona sahip olun ve sütun sayısı değişken sayısına karşılık gelecektir

$(x_1, x_2, \ldots , x_n).$

Öte yandan bu matris Jacobian diferansiyel haritası veya Jacobian doğrusal haritası olarak da bilinir. Hatta bazen J harfi yerine D harfiyle de yazılıyor:

$\displaystyle J_f = D_f$

İlginç bir şekilde, Jacobian matrisi, adını özellikle doğrusal cebir alanında matematik dünyasına önemli katkılarda bulunan, 19. yüzyılın önemli matematikçisi ve profesörü Carl Gustav Jacobi’den almıştır.

Jacobian matrisini hesaplama örneği

Jacobian matrisi kavramını gördükten sonra, bir örnek kullanarak adım adım nasıl hesaplandığını göreceğiz:

Aşağıdaki fonksiyonun (1,2) noktasındaki Jacobian matrisini belirleyin:

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

Yapmamız gereken ilk şey, fonksiyonun tüm birinci dereceden kısmi türevlerini hesaplamaktır:

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

Şimdi Jacobian matris formülünü uyguluyoruz. Bu durumda, fonksiyonun iki değişkeni ve iki skaler fonksiyonu vardır, dolayısıyla Jacobian matrisi 2×2 boyutunda bir kare matris olacaktır:

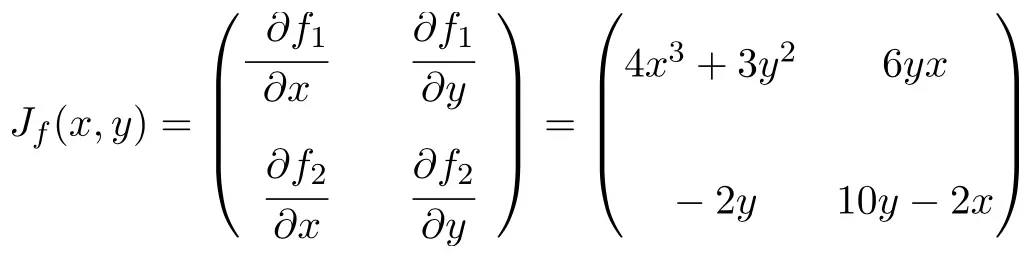
Jacobian matrisinin ifadesini elde ettikten sonra onu (1,2) noktasında değerlendiririz:

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

Ve son olarak işlemleri gerçekleştirip çözüme ulaşıyoruz:

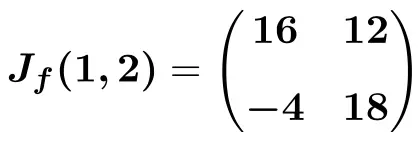
Bir fonksiyonun Jacobian matrisini nasıl bulacağınızı gördükten sonra, pratik yapabilmeniz için size adım adım çözülmüş birkaç alıştırma bırakıyoruz.

Jacobian matrislerinin çözülmüş problemleri

1. Egzersiz

2 değişkenli aşağıdaki vektör fonksiyonunun (0,-2) noktasındaki Jacobian matrisini bulun:

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

Çözüme bakın

Fonksiyonun iki değişkeni ve iki skaler fonksiyonu vardır, dolayısıyla Jacobian matrisi 2×2 boyutunda bir kare matris olacaktır:

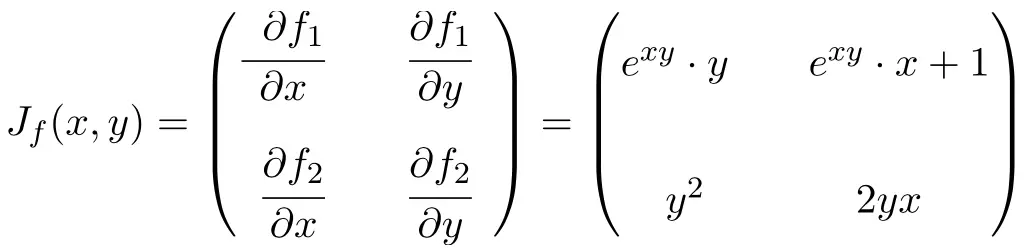
Jacobian matrisinin ifadesini hesapladıktan sonra onu (0,-2) noktasında değerlendiririz:

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

Ve son olarak işlemleri gerçekleştiriyoruz ve sonucu elde ediyoruz:

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

Alıştırma 2

2 değişkenli aşağıdaki fonksiyonun (2,-1) noktasındaki Jacobian matrisini hesaplayın:

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

Çözüme bakın

Bu durumda, fonksiyonun iki değişkeni ve iki skaler fonksiyonu vardır, dolayısıyla Jacobian matrisi 2. dereceden bir kare matris olacaktır:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

Jacobian matrisinin ifadesini bulduğumuzda, onu (2,-1) noktasında değerlendiririz:

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

Ve son olarak işlemleri gerçekleştiriyoruz ve sonucu elde ediyoruz:

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

Alıştırma 3

Aşağıdaki 3 değişkenli fonksiyonun (2,-2,2) noktasındaki Jacobian matrisini belirleyin:

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

Çözüme bakın

Bu durumda, fonksiyonun üç değişkeni ve iki skaler fonksiyonu vardır, dolayısıyla Jacobian matrisi 2×3 boyutunda dikdörtgen bir matris olacaktır:

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

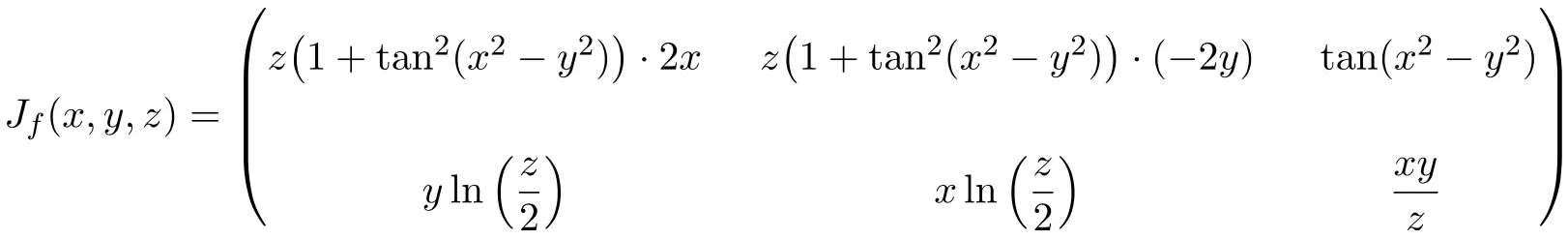
Jacobian matrisi 3 değişkenli alıştırmayı çözdü

Jacobian matrisinin ifadesini elde ettikten sonra onu (2,-2,2) noktasında değerlendiririz:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

Hesaplamaları yapıyoruz:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

Ve artık basitleştirilemeyecek duruma gelene kadar çalışmaya devam ediyoruz:

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

Alıştırma 4

Bu noktada Jacobian matrisini belirleyin

$(\pi, \pi)$

aşağıdaki çok değişkenli fonksiyondan:

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

Çözüme bakın

Bu durumda, fonksiyonun iki değişkeni ve üç skaler fonksiyonu vardır, dolayısıyla Jacobian matrisi 3×2 boyutunda dikdörtgen bir matris olacaktır:

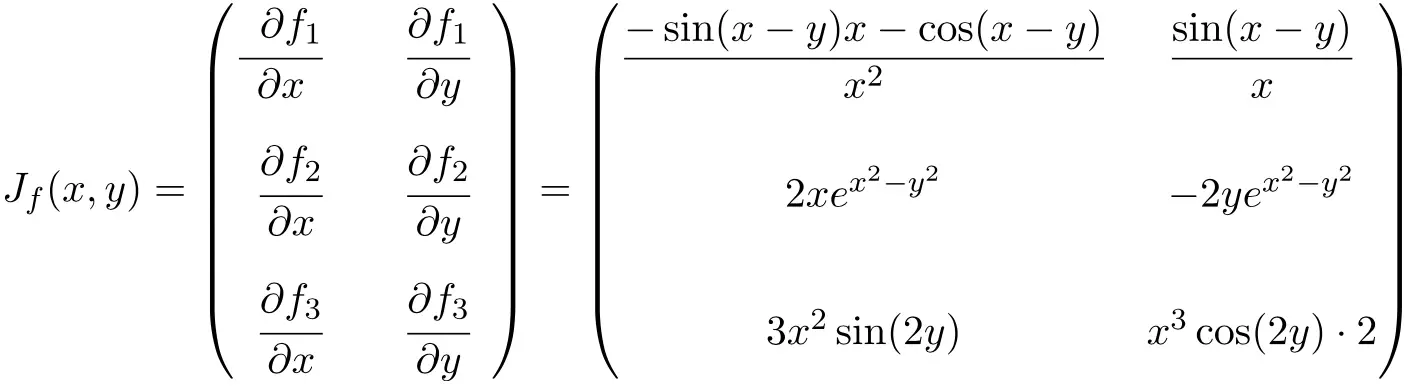
alıştırma Jacobian matrisinin adım adım çözüldü

Jacobian matrisinin ifadesini elde ettiğimizde, onu şu noktaya kadar değerlendiririz:

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

Operasyonları gerçekleştiriyoruz:

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

Dolayısıyla, dikkate alınan noktadaki vektör fonksiyonunun Jacobian matrisi şu değerdedir:

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

Alıştırma 5

Bu noktada Jacobian matrisini hesaplayın

$(3,0,\pi)$

3 değişkenli aşağıdaki fonksiyondan:

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

Çözüme bakın

Bu durumda fonksiyon üç değişkenli ve üç skaler fonksiyondan oluşur, dolayısıyla Jacobian matrisi 3×3 boyutunda bir kare matris olacaktır:

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

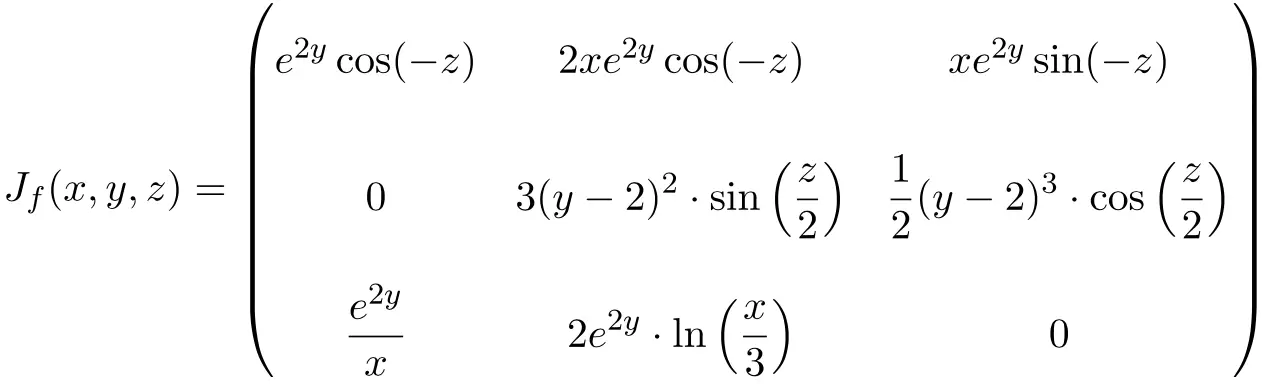
3 değişkenli 3x3 Jacobian matrisinin çözülmüş alıştırması

Jacobian matrisini bulduktan sonra onu şu noktada değerlendiririz:

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

İşlemleri hesaplıyoruz:

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

Ve Jacobian matrisinin bu noktadaki sonucu:

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

Jacobian matrisinin determinantı: Jacobian

Jacobian matrisinin determinantına Jacobian determinantı veya Jacobian denir. Jacobian’ın yalnızca fonksiyonun skaler fonksiyonlarla aynı sayıda değişkene sahip olması durumunda hesaplanabileceği dikkate alınmalıdır, çünkü bu durumda Jacobian matrisi sütunlarla aynı sayıda satıra sahip olacak ve bu nedenle bir kare olacaktır. matris. .

Jakoben örneği

İki değişkenli bir fonksiyonun Jacobian determinantını hesaplamanın bir örneğini görelim:

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

İlk önce fonksiyonun Jacobian matrisini hesaplıyoruz:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

Şimdi 2×2 matrisin determinantını çözüyoruz:

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

Jacobian ve bir fonksiyonun tersinirliği

Artık Jacobian kavramını gördüğünüze göre muhtemelen şunu düşünmüşsünüzdür… peki ne anlamı var?

Jacobian’ın asıl kullanımı, bir fonksiyonun tersine çevrilip çevrilemeyeceğini belirlemektir. Ters fonksiyon teoremi, Jacobian matrisinin determinantının (Jacobian) 0’dan farklı olması durumunda, bu fonksiyonun tersinir olduğu anlamına geldiğini söyler.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

Bu koşulun gerekli ancak yeterli olmadığını belirtmek gerekir, yani determinant sıfırdan farklıysa matrisin ters çevrilebileceğini iddia edebiliriz ancak determinant 0 ise matrisin ters çevrilebileceğini iddia edebiliriz. fonksiyonun tersi veya No’su vardır.

Örneğin, bir fonksiyonun Jacobian’ının nasıl bulunacağına ilişkin daha önce görülen örnekte determinant şunu verir:

$4x^2+4y^2$

. Bu durumda fonksiyonun (0,0) noktası dışında her zaman tersine çevrilebileceğini iddia edebiliriz, çünkü bu nokta Jacobian determinantının sıfıra eşit olduğu tek noktadır ve bu nedenle ters fonksiyonun olup olmadığını bilmiyoruz. bu noktada bulunmaktadır.

Jacobian matrisinin diğer işlemlerle ilişkisi

Jacobian matrisi, bir fonksiyonun gradyanı ve Hessian matrisi ile ilgilidir:

Eğim

Eğer fonksiyon bir skaler fonksiyon ise, Jacobian matrisi, gradyana eşdeğer olan bir satır matrisi olacaktır:

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

Hessian matrisi

Bir fonksiyonun gradyanının Jacobian matrisi Hessian matrisine eşittir:

$\displaystyle H_f = J(\nabla f)$

Hessian, fonksiyonun ikinci türevlerinden oluştuğu için birden fazla değişkenli fonksiyonların türetilmesinde çok önemli bir matristir. Aslında Hessian matrisinin Jacobian matrisinin sürekliliği olduğu söylenebilir. Ancak bunu ayrıntılı olarak açıklayan bir sayfamızın olması çok önemli. Peki bu matrisin tam olarak ne olduğunu ve neden bu kadar özel olduğunu bilmek istiyorsanız bağlantıya tıklayabilirsiniz.

Jacobian matrisinin uygulamaları

Bir fonksiyonun tersinir olup olmadığını belirleyen Jacobian’ın kullanışlılığının yanı sıra, Jacobian matrisinin başka uygulamaları da vardır.

Jacobian matrisi, çok değişkenli bir fonksiyonun kritik noktalarını hesaplamak için kullanılır; bunlar daha sonra Hessian matrisi aracılığıyla maksimum, minimum veya eyer noktaları olarak sınıflandırılır. Kritik noktaları bulmak için fonksiyonun Jacobian matrisini hesaplamanız, 0’a eşitlemeniz ve elde edilen denklemleri çözmeniz gerekir.

$\displaystyle J_f(x)=0$

Ek olarak, Jacobian matrisinin başka bir uygulaması, birden fazla değişkenli fonksiyonların (ikili, üçlü integraller vb.) entegrasyonunda bulunur. Jacobian matrisinin determinantı, aşağıdaki formüle göre çoklu integrallerdeki değişkenin değişmesine izin verdiğinden:

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

Burada T, orijinal değişkenleri yenileriyle ilişkilendiren değişken değişim fonksiyonudur.

Son olarak, Jacobian matrisi herhangi bir fonksiyonun doğrusal bir yaklaşımını yapmak için de kullanılır.

$f$

bir nokta civarında

$p$

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

Jacobian ve jacobian matrisi

Jacobian matrisi nedir?

Jacobian matrisini hesaplama örneği

Jacobian matrislerinin çözülmüş problemleri

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Jacobian matrisinin determinantı: Jacobian

Jakoben örneği

Jacobian ve bir fonksiyonun tersinirliği

Jacobian matrisinin diğer işlemlerle ilişkisi

Eğim

Hessian matrisi

Jacobian matrisinin uygulamaları

Yorum bırakın Yanıtı iptal et